滚针轴承接触分析

王爱林，洪玉芳，汪久根

(浙江大学 机械工程学系，杭州 310027)

滚针轴承的径向尺寸小，广泛应用于结构紧凑的场合，例如万向节传动中。滚针轴承的疲劳寿命是其主要问题，评价滚针轴承疲劳的各种模型中，采用的应力有最大剪应力、最大正交剪应力和Mises应力[1-2]。另外，滚针轴承在使用过程中经常发生滚针的断裂，这一般是由于滚针的偏载引起的。因此，研究滚针轴承的疲劳寿命和偏载问题具有实际的工程意义。

1 数学模型

1.1 弹性接触模型

滚针与滚道的接触属于非Hertz弹性接触问题。将滚针与滚道作为两弹性体，其在径向载荷Fr作用下产生弹性变形并形成接触区域Ω。定义δ为两弹性体之间产生的弹性趋近量，则

ω1+ω2+f1+f2=δ，

(1)

式中：ω1，ω2分别为滚针和内滚道在接触点的弹性变形；f1，f2分别为滚针表面和内滚道表面在加载变形前距名义接触点切线的垂直距离。

ω1,ω2可由Boussinesq公式来求解，即

dsdt，

(2)

同时，根据平衡条件有

(3)

则，(1)和(3)式构成了滚针与滚道接触问题的基本方程。根据结构分析中的影响系数法，可将接触区域划分为多个单元。在滚针速度方向和滚针素线方向划分50×50的网格单元，在每个单元格上假设接触应力恒定，然后将 (1)式～(3) 式离散成线性方程组，在法向应力分布p(s,t)和切向摩擦力分布F(s,t)联合作用下，得到总的Mises应力。由此可以计算出滚道内部的最大切应力以及其深度，从而得出疲劳失效的起源点。

1.2 滚针与滚道间的弹性趋近量

在求取滚子与滚道接触的弹性趋近量时，最常用的是Palmgren给出的经验公式，即

(4)

式中：Q为滚动体载荷；Lwe为滚子有效长度。

在(4)式中，表面的弹性趋近量与滚子和滚道的直径无关。文献[3]从有限长线接触问题的数值解的角度说明了Palmgren公式的局限性，指出弹性趋近量除与滚动体载荷及滚子有效长度相关外，还与滚子和滚道的当量直径有关；并分析了圆柱滚子轴承，得出了Palmgren公式的修正结果，即

(5)

1/D=1/Dw±1/dr，

式中：D为同时考虑滚子与滚道曲率的当量直径；Dw为滚子直径；dr为滚道直径;符号“+”用于内滚道直径；符号“-”用于外滚道直径。

针对滚针轴承，还需要对上式进行修正。取弹性趋近量的计算公式如 (6)式所示，其中a1，a2，a3，a4为待定系数。

(6)

分别对Q，D和Lwe取4个值，通过正交表L16(45)，进行了16次试验，再选用最小二乘法对4个系数进行拟合，得到了GCr15钢制滚针轴承滚针与滚道间的弹性趋近量为

(7)

1.3 滚针偏斜分析

滚针偏斜的示意图如图1所示。在径向平面内滚子轴线与套圈滚道素线产生一个角度。根据力矩平衡原理，此时接触力的合力P距滚针中心的距离为e，弯矩W=Pe。 随着偏斜角β的增加，弯矩不断增大，由此计算出的弯曲应力σ也相应增大，当弯曲应力超过GCr15钢的抗拉强度极限σb时，滚针将发生断裂。

图1 滚针偏斜示意图

1.4 滚子偏斜对轴承疲劳寿命的影响

文献[4]提出轴承疲劳寿命L10降低20%时，圆柱滚子允许的临界偏斜角为

(8)

式中：Fr为轴承所受径向载荷；C0为轴承额定静载荷。

结合(5) 式，根据文献[4]的方法推导出圆柱滚子轴承疲劳寿命降低20%时的临界偏斜角为

(9)

由(7)式和(9)式可以得出滚针轴承疲劳寿命降低20%时的临界偏斜角为

(10)

随着滚针偏斜角度的增加，接触表面应力分布情况和表面层Mises应力场将随之发生变化。Lundberg和Palmgren提出的材料疲劳破坏概率的经验公式为

(11)

式中：S为存活概率；τ0为最大动态剪切应力；z0为最大动态剪切应力所在深度；N为应力循环次数，以百万次计；V为受应力的体积。 根据Ioannides E 和Harris T A疲劳寿命模型[5]，并结合(11)式可通过比例关系来计算不同偏斜角下轴承的相对疲劳寿命。

2 计算结果及分析

所选研究对象中所需各参数为：内圈滚道直径F为40 mm,滚针直径Dw为5 mm,滚针有效长度Lwe为13 mm，滚针和内圈材料为GCr15钢，其抗拉强度极限σb为735 MPa，单个滚针所加径向载荷为4 250 N，滚针与滚道间的摩擦因数取0.08。

2.1 滚针偏斜对滚针磨损和断裂的影响

在此对滚针偏斜角为β=0～0.07°、间隔为0.01°的每个偏斜角取值情况下的接触应力分布和Mises应力分布进行计算。

滚针无偏斜(β=0)时的接触应力分布和Mises应力分布如图2和图3所示。图中x代表滚针滚动方向；y代表滚针素线方向；z代表轴承滚道表面层深度；滚针与滚道接触表面的中心点为坐标原点。由图2可知，接触应力沿滚针中间截面对称分布，在其端部有很明显的应力集中。由计算可知，滚针端部的最大接触应力达到3.11 GPa，而滚针中部的最大接触应力为2.24 GPa，滚针轴承滚道接触表面层的最大Mises应力为596 MPa，出现在深度为0.117 mm处。

图2 β=0时接触应力场

图3 β=0时接触表面层的Mises应力场(GPa)

滚针偏斜角β分别为0.04°和0.07°时，接触应力场和Mises应力计算结果如图4～图7所示。

图4 β=0.04°时接触应力场

图5 β=0.04°时接触表面层的Mises应力场(GPa)

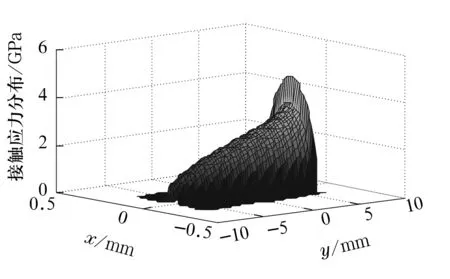
图6 β=0.07°时接触应力场

图7 β=0.07°时接触表面层的Mises应力场(GPa)

由图可知，滚针两端最大接触应力之差随着偏斜角的增大而增大。由计算可知，当β=0.04°时，两端接触应力分别为2.01 GPa和4.03 GPa，即一端应力已达到另一端的2倍，此时在高的接触应力端滚针轴承会发生严重的局部磨损。当β=0.07°时，弯曲应力σ的值达到825 MPa，高于GCr15钢的抗拉强度极限σb(735 MPa)，说明此时滚针会发生断裂。 由计算结果可知，在偏斜角度增大的过程中，接触区表面层的最大Mises应力值会不断增大，但最大Mises应力出现的位置保持不变，一直在深度为0.117 mm处。

2.2 不同偏斜角下轴承的相对疲劳寿命

根据Ioannides E 和Harris T A疲劳寿命模型[5]，并结合(11)式，用接触表面层的最大Mises应力代替最大动态剪切应力，计算出滚针不同偏斜角下轴承的相对疲劳寿命(表1)。

表1 滚针不同偏斜角下轴承的相对疲劳寿命

由表1可知，表面层内最大Mises应力随着滚针偏斜角的增大而增大，但其最大值出现的深度一直不变；而滚针轴承接触疲劳寿命则随偏斜角的增加急剧降低。

3 结论

(1)当滚针偏斜角和两端接触应力值达到一定程度，滚针轴承开始出现严重磨损，甚至滚针会出现断裂。 表面层内最大Mises应力随着滚针偏斜角的增大而增大，但其最大值出现的深度一直不变。

(2) 随着滚针偏斜角的增大，其滚动接触疲劳寿命急剧降低。