匀速圆周运动向心加速度的教学研究

何述平

(西北师范大学教育学院物理教育研究所,甘肃兰州 730070)

1 引言

现行普通高中课程标准实验教科书物理2通过“做一做:探究向心加速度大小的表达式”[1]、“多学一点:推导向心加速度公式”[2],运用速度矢量方法以拓展形式推得匀速圆周运动向心加速度的表达式;另外也有运用运动合成与分解方法[3][4]推得的.此外,还能想到怎样的推导方法?这些方法有何物理学方法论的特色?又有什么物理教学特点?能否引入位置矢量从而更好地理解匀速圆周运动的向心加速度并体现物理科学探究要素的教学?本文就此作探讨,并期望对可能的疑惑进行解释,为普通高中物理关于匀速圆周运动向心加速度的开放探究式教学设计奠定必要的理论基础.

2 探讨

2.1 向心加速度推导方法的概括

将见到、想到的匀速圆周运动向心加速度表达式的推导方法概括如下.

2.1.1 速度矢量法

如图1,质点绕圆心O做半径r、速率 v的匀速圆周运动,经过时间Δt,沿圆周由 A点运动到B点,半径相应扫过圆心角Δθ,速度 vA、vB分别与半径rA、rB垂直,且沿圆周切向.如图2,速度 vA、vB和改变量Δv=vB-vA构成速度矢量三角形.由速度矢量三角形与圆周三角形的相似关系或夹角关系可推得匀速圆周运动向心加速度的表达式.

(1)相似关系方式[1][2]

由图1、2的几何关系知,速度矢量三角形与圆周三角形 AOB相似,有

当Δt足够短或趋于零时,有

由式(1)～(3)式得

式(4)为匀速圆周运动向心加速度大小的表达式.

由图1、2知Δt趋于零时,Δθ趋于零,Δv垂直于vA,即匀速圆周运动向心加速度 an的方向沿圆周半径指向圆心,且与速度 vA垂直.

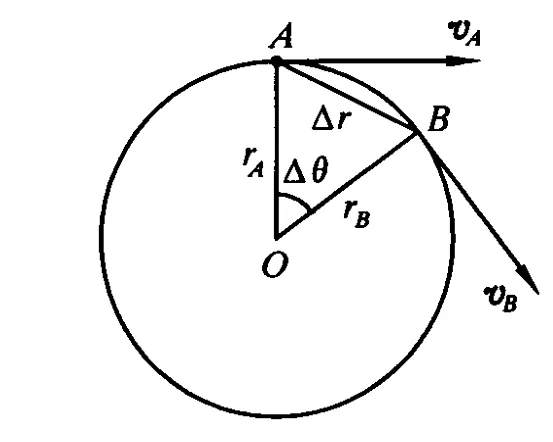
图1

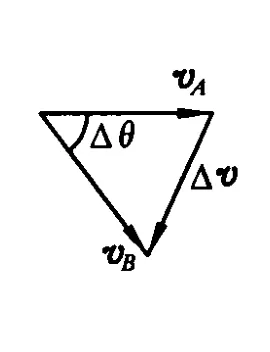
图2

(2)夹角关系方式

对图1、2,当Δt足够短或趋于零时,有

再结合式(2)、(3)式,得 an表达式,结果同式(4);同理推知an的方向.

2.1.2 运动合成法

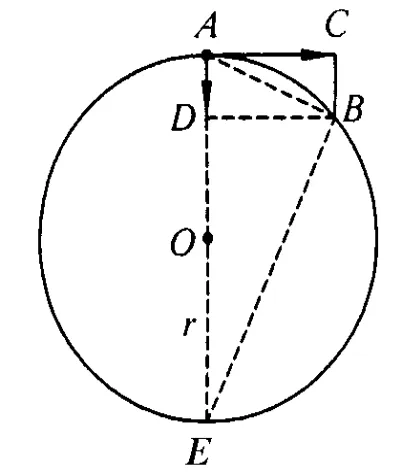
图3

如图3,质点绕圆心O做半径r、速率v的匀速圆周运动,经过时间Δt,沿圆周由A点运动到B点.按照运动合成与分解的方法,可以将匀速圆周运动看作沿着速度方向 A→C的匀速直线运动和沿半径指向圆心A→D的初速度为零的匀加速直线运动的合运动.

(1)运动合成法的方式Ⅰ[3]

或AB2=AD◦AE.当Δt足够短或趋于零时,有

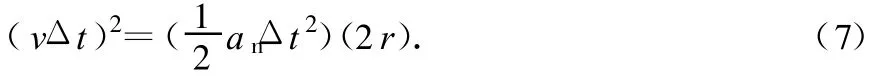
解得 an表达式,结果同式(4).

(2)运动合成法的方式Ⅱ

由图3的几何关系知:△ADB∽△BDE,有 AD/DB=DB/DE 或DB2=AD◦DE,即

Δt有唯一解,得 an表达式,结果同(4)式.

2.1.3 运动分解法[4]

图4

如图4,质点绕圆心 O做半径r、速率 v的匀速圆周运动,经过时间 Δt,沿圆周由 A点运动到B点.按照运动分解与合成的方法,可以将匀速圆周运动分解为沿着速度方向 A→P的匀速直线运动和指向圆心P→B的初速度为零的匀加速直线运动.依据平面几何的切割线定理(圆外一点P引圆的切线PA、过圆或圆心的割线 PBC)有 PA2=PB◦PC,即

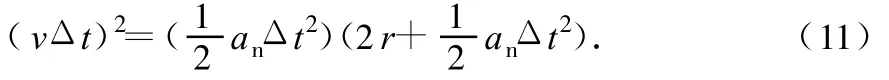
与(8)式同理,得 an的表达式,结果同(4)式.

2.2 向心加速度推导方法的比较

从物理学方法论看,速度矢量法、运动合成法、运动分解法均是推导向心加速度的运动学方法.具体为:速度矢量法是物理概念(速度概念、加速度概念)方法、数学方法(几何相似法或弧度夹角法、极限方法)的结合;运动合成法的方式Ⅰ是物理概念(匀速圆周运动线速度概念)方法、物理规律(匀变速直线运动规律)方法、数学方法(几何相似法、极限方法、代数方程法)的结合;运动合成法的方式Ⅱ是物理规律(匀速直线运动规律、匀变速直线运动规律)方法、数学方法(几何相似法、代数方程法)的结合;运动分解法是物理规律(匀速直线运动规律、匀变速直线运动规律)方法、数学方法(几何切割线定理法、代数方程法)的结合.

从物理教学方法看,仅仅因速度矢量方向变化引起向心加速度(这是直线运动中所没有的情形)是教学难点(为了降低教学难度,先从未称谓的向心力与向心加速度的关系即从动力学推出向心加速度的方向,再从运动学推得向心加速度大小的表达式[1][2]).因此,速度矢量法是直接依据物理概念的基本方法,是教学难度最大的方法.运动合成法的方式Ⅰ是直接运用物理概念、规律的方法,是教学难度适中的方法;运动合成法的方式Ⅱ是直接运用物理规律的方法,是教学难度最小的方法;然而为什么是那样的运动合成似乎欠明确.运动分解法是直接运用物理规律的方法,也是教学难度最小的方法;然而为什么是那样的运动分解似乎欠明确.

2.3 向心加速度的释疑解惑

匀速圆周运动向心加速度的教学中,可能存在以下一些疑惑;而疑惑的解决有益于提高中学物理教学设计的效率和水平.

2.3.1 对于速度矢量法,推导向心加速度表达式过程中的关系式是近似式还是准确式?表示的是平均物理量还是瞬时物理量?

Δt一定或有限时,式(5)、(6)是近似式;式(2)、(3)表示的是平均物理量;式(4)表示的是平均物理量(但等于瞬时物理量).Δt足够短或趋于零时,式(5)、(6)是准确式;式(2)、(3)表示的是瞬时物理量;式(4)表示的是瞬时物理量.

另外,无论Δt是一定还是趋于零,式(1)均是准确式.2.3.2 对于运动合成法、运动分解法,为什么是那样的运动合成、分解?

图4中,将A→B的匀速圆周运动想象或理解为:A→P的惯性运动即匀速直线运动和P→B的向心力(大小恒定)作用下的自由落体运动即指向圆心的初速度为零的匀加速直线运动[5].运动合成法意味着同时进行这两种运动,运动分解法意味着依次进行这两种运动.

2.3.3 为什么不将匀速圆周运动像平抛运动那样进行运动分解来研究?

将匀速圆周运动与平抛运动对比,以明确异同点,或许有助于此疑惑的解决.

(1)运动特点.

(2)受力特点.

匀速圆周运动、平抛运动分别是变力(大小恒定、方向变化,即向心力;向心力是等效力)和恒力(大小、方向均恒定,即重力)的作用.

(3)能量特点

匀速圆周运动的向心力、平抛运动的重力分别不做功和做功,但机械能却都守恒,匀速圆周运动的能量形式(即动能)不变,平抛运动的能量形式(即动能和势能)转化.

基于上述特点的对比,并虑及选择坐标系应使问题研究简化的原则,研究匀速圆周运动不宜选取像研究平抛运动那样的平面直角坐标系即恒定坐标系,而应选取切-法向坐标系即变动坐标系(选择平面直角坐标系也未尝不可,只是繁琐而已或超出现行普通高中物理范围;不妨一试,或许认识深些[6]).因此,一般不宜将匀速圆周运动像平抛运动那样进行运动分解来研究.

2.4 向心加速度的教学建议

2.4.1 基本建议

依据2.2.2和2.3.2,虽然速度矢量法、运动合成法的方式Ⅰ、运动合成法的方式Ⅱ、运动分解法等匀速圆周运动向心加速度的推导方法各有侧重,但是其教学难度则依次递减.这样可根据教师、学生的水平和具体教学目标,灵活选择有效的推导方法,进而再设计可行的教学方式(如探究式、讨论式,等等).

2.4.2 提高建议

依据匀速圆周运动的轨迹特点,引入位置矢量[7]或许对理解线速度、角速度、向心加速度以及相互关系更有益,且含有利于教学的类比、猜测、论证等物理科学探究的要素.

质点绕圆心O做半径r、速率 v的匀速圆周运动,经过时间Δt,沿圆周由 A点运动到B点;相应位置矢量rA、rB,位移Δr=rB-rA,位置矢量扫过角Δθ,速度矢量 vA、vB(分别与相应位置矢量垂直)和改变量Δv=vB-vA,如图5.

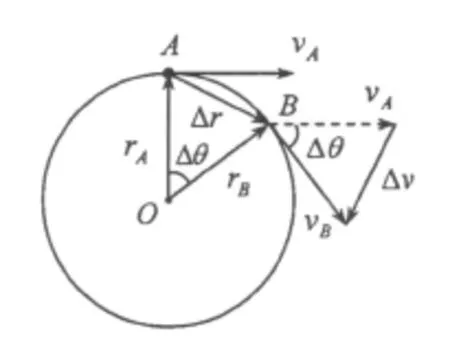
图5

Δt足够短或趋于零时,有

由式(12)～(14)得

式(16)是线速度 v、角速度 ω、位置矢量 r的大小关系.

图5中的位置矢量和式(12)表明:速度矢量v是位置矢量r仅因方向变化而引起,是位置矢量的时间变化率;且v与r垂直.图5中的速度矢量和式(15)表明:加速度矢量an是速度矢量v仅因方向变化而引起,是速度矢量的时间变化率.类比两者(注意:方向变化皆因旋转),猜测与式(16)类似的关系,有

且 an与 v垂直.由式(16)、(17)得

然后,再依据速度矢量三角形与位置矢量三角形的相似,按照2.1.1的速度矢量法进行论证.

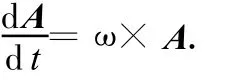
3 问题分析

作为方法的运用,分析以下平面曲线运动的加速度问题并关注分析方法.

3.1 问题[8]

有一只狐狸以不变的速度v1沿直线 AB逃跑,一只猎犬以不变的速率 v2追击,其运动方向始终对准狐狸.某时刻狐狸在 D处,猎犬在 C处,且 CD⊥AB,CD=L,如图6.试求此时猎犬的加速度大小.

图6

3.2 分析方法

3.2.1 中学物理方法

图7

狐狸视作质点,做匀速直线运动;猎犬视作质点,做变速曲线运动.始终对准意味着 v2方向始终指向狐狸.经过时间Δt,狐狸沿直线 AB的位移是v1Δt;猎犬速度 v2方向改变角Δφ,速度矢量三角形与位置三角形如图7.

Δt足够短或趋于零时,由图7有

由式(19)～(21)得

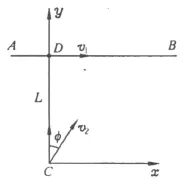
图8

方向沿水平向右.这样运用速度矢量法解决了变速平面曲线运动的加速度问题.

3.2.2 普通物理方法

分析同前,建立直角坐标系,如图 8.t=0时,x1=0,y1=L;v2x=0,v2y=v2.

经过时间 t,速度v2方向改变角 φ,此时由图8分别对猎犬和狐狸有

对时间 t求导,由式(23)～(25)得

t=0时,加速度大小为

方向沿x轴正向.这样运用普通物理方法(加速度概念法、三角函数法和导数法)解决了变速平面曲线运动的加速度问题.

4 结语

本文的匀速圆周运动向心加速度推导方法的概括、比较,突出了物理学方法论的特色、物理发散思维的特征,分析得出了物理教学的特点,奠定了匀速圆周运动向心加速度教学设计的理论基础,并为物理科学方法教育提供了较详细的要素;释疑解惑加深了对匀速圆周运动向心加速度推导方法的认识;教学建议提供了教学基本选择依据和教学提高拓展空间,可作为匀速圆周运动向心加速度教学深入和开放的实例;变速平面曲线运动加速度问题的分析表明了不同层次方法的运用,是加速度分析方法的活化.

1 人民教育出版社课程教材研究所,物理课程教材研究开发中心.普通高中课程标准实验教科书物理2.北京:人民教育出版社,2006(第2版).18

2 束炳如,何润伟.普通高中课程标准实验教科书物理2.上海:上海科技教育出版社,2007(第2版).27

3 陈刚,舒信隆.新编物理教学论.上海:华东师范大学出版社,2006.258-259

4 廖伯琴.物理教学研究与案例.北京:高等教育出版社,2006.62

5 Art Hobson.物理学:基本概念及其与方方面面的联系.秦克诚等译.上海:上海科学技术出版社,2001.109-111

6 Kleppner D,Kolenkow R J.力学引论.宁远源等译.北京:人民教育出版社,1980.23-24,32-34

7 Zitzewitz PW.科学发现者:物理原理与问题(上册).钱振华等译.杭州:浙江教育出版社,2008.167-168

8 阎金铎,田世昆.中学物理教学概论.北京:高等教育出版社,1991.299-300