巧用时钟转动模型,速解天体追及问题

黄江铭

(浙江省新昌澄潭中学,浙江新昌 312500)

天体的追及问题是学生学习的难点,如何突破这个难点呢?实践表明,应用学生容易理解的“时钟转动模型”能顺利解决这类问题.

1 时钟转动模型

例1.12点整时,钟面上的时针、分针刚好重合,如图1所示.请你计算一下,再过多长时间,钟面上的时针与分针再次重合?

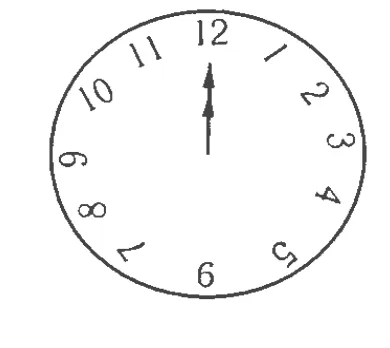
图1

图2

解析:由于分针比时针转得快,当分针转动1周时,时针才转动1格,接下去是分针去追赶时针,最后在某个位置又再次重合,如图2所示.

不难发现,分针与时针再次重合,分针比时针多转动1周,并且运动的时间又相同,因此,我们可得出以下式子

其中φ表示时针转过的弧度,ω1表示分针转动的角速度,ω2表示时针转动的角速度.

其中分针转1周的时间T1=12 h,时针转1周的时间T2=1 h.

联立(1)、(2)式,化简为

总之,代入数据,可得

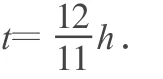
时针和分针(或者分针和秒针)再次重合时,存在着以下关系式

2 应用时钟转动模型,解决天体追及问题

例2.如图3所示,火星和地球绕太阳的运动可以近似看作在同一平面内同方向的匀速圆周运动,已知火星的轨道 r1=2.3×1011m,地球的轨道半径 r2=1.5×1011m,从图示的火星与地球相距最近的时刻开始,试估算火星再次与地球相距最近需多长时间.(以年为单位计算)

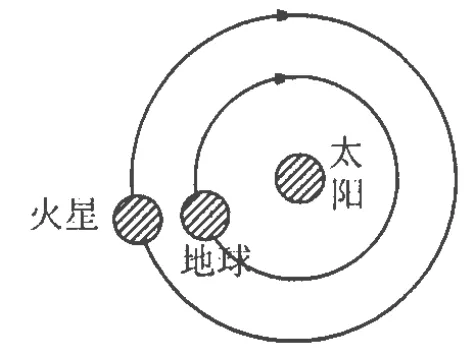
图3

解析:行星绕太阳做近似匀速圆周运动,有

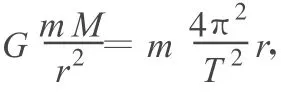
可得

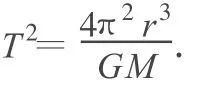
所以

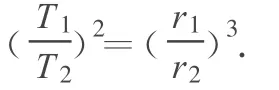
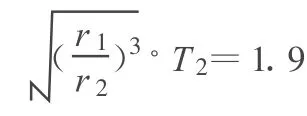
火星转得慢,地球转得快,要再次相遇,地球比火星多转1周,运动情况与“时钟转动模型”相同.

根据“时钟转动模型”的导出式(Ⅰ),

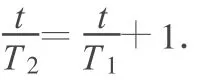
其中 T1表示火星绕太阳转动的周期,T2表示地球绕太阳转动的周期.可得t=2.1年.

例3.假设有一载人宇宙飞船在距地面高度为4 200 km的赤道上空绕地球做匀速圆周运动,地球半径约为6 400km,地球同步卫星距地面高度为36 000 km,宇宙飞船和地球同步卫星绕地球同向运动,每当二者相距最近时,宇宙飞船就向同步卫星发射信号,然后再由同步卫星将信号发送到地面接收站,某时刻二者相距最远,从此刻开始,在一昼夜的时间内,接收站共接收到信号的次数为

(A)4次. (B)6次. (C)7次. (D)8次.

其中R1、R2分别是同步卫星和宇宙飞船的轨道半径;T1、T2分别是同步卫星和宇宙飞船的运动周期.代入数据,可得

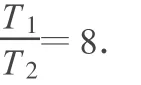
开始时刻,宇宙飞船、同步卫星和地球的位置如图4所示,第1次接收到信号时,宇宙飞船、同步卫星和地球的位置如图5所示,宇宙飞船比同步卫星多转动0.5圈.

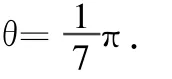
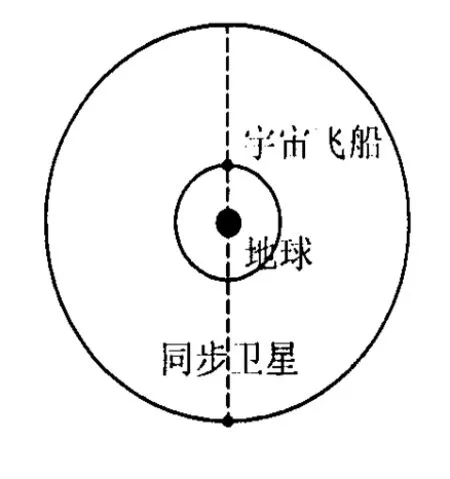
图4

图5

第2次接收到信号时,宇宙飞船、同步卫星和地球的位置如图6所示,宇宙飞船比同步卫星多转动1圈.

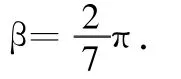
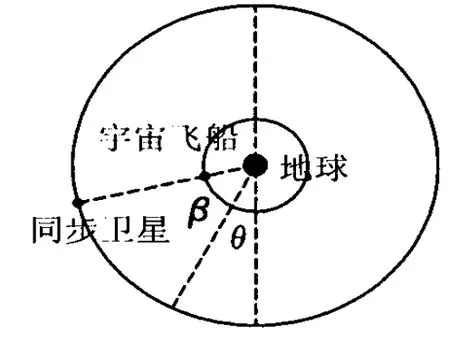
图6