基于SCEM-UA算法和全局敏感性分析的水文模型参数优选不确定性研究*

曹飞凤，张世强，许月萍，楼章华

(1.浙江省水利水电工程局，浙江 杭州 310020；2.浙江大学 建筑工程学院水文与水资源工程研究所，浙江 杭州 310058；3.中国科学院寒区旱区环境与工程研究所，甘肃 兰州 730000)

水文模型参数的非线性和相关性导致参数分布存在多个局部最优解和不连续可导点，采用传统的贝叶斯算法推求其显性联合概率分布十分困难，而Markov链蒙特卡罗法(Markov Chain Monte Carlo，MCMC)较传统的统计方法(如矩估计法，极大似然估计法等)能更好的处理非线性复杂问题的求解，因此，近年来被广泛应用于流域水文模型参数后验分布的推算[1-6]。

Duan等[7]提出的SCE-UA算法致力于高效且具鲁棒性的搜索参数全局最优解，许多研究都证明了SCE-UA算法的高效性[8-9]，但是该算法容易将搜索范围聚焦到单个最佳参数周围的小区域而陷入局部最优[10]。SCE-UA算法与其他传统参数优选方法一样更多关注参数优化的效率问题，而对模型参数的不确定性分析较为缺乏。由于水文数据和模型本身都有一定的置信区间，只关注参数优化效率而忽视对模型输入、参数及结构等的不确定性分析，将导致模型输出缺乏可靠性。基于上述考虑，Vrugt等[10]提出用MCMC理论的自适应Metropolis算法[11]取代SCE-UA算法中的坡降单纯形法，形成了SCEM-UA (Shuffled Complex Evolution Metropolis-UA)参数全局优化算法。该算法采用自适应Metropolis采样器，使新样本的推荐分布不仅仅依靠先验分布，而是在计算过程不断更新，从而使该算法的计算效率大大提高，并能够有效获取参数的后验概率分布。RSA(Regional Sensitivity Analysis)是全局敏感性分析的一种重要方法，由Hornberger和Spear于1981年提出的[12]，该方法侧重分析参数空间分布的复杂性与相关性对模型输出的响应，已被广泛应用于水文模型参数的敏感性分析。如何将优化算法与参数的敏感性分析相结合，进一步提高模型参数优化的效率和可靠性，是目前水文模型研究方面的一个热点。本文以岷江流域为案例，基于SCEM-UA算法和RSA方法研究了水文模型参数的后验分布和不确定性，并在最后给出了置信区间为90%的模拟结果。

1 SCEM-UA算法

1.1 参数后验概率密度估计

降雨径流模型的不确定性主要包括输入的不确定、参数的不确定和模型结构的不确定性[13]。考虑到模型误差来源很难被定量化，一般常用如式(1)所示的简单集总变量来表示，式中y代表模型输出的N×1维向量；ε代表模型输入的N×r维矩阵；θ代表n个模型参数向量。因此，对公式(1)问题的优化就转化为求解E(θ)={e(θ)1,e(θ)2,…,e(θ)N}的最小解问题。假设残差e(θ)相互独立并服从高斯分布，可推求参数θ(t)的似然度，如式(2)所示，式中，λ表示残差的分布类型，推导过程中取λ=0，即表示残差服从正态分布；σ为残差序列方差，∝表示正比于，假设p(θ)∝σ-1，可进一步求得如式(3)所示的θ(t)后验概率密度[14]。

y=f(ε|θ)+e

(1)

(2)

(3)

1.2 算法原理

1.3 SCEM-UA算法的参数设置

(4)

2 案例研究

2.1 数据

本文选取岷江高场站以上流域作为研究例子。流域面积为135 400 km2，多年平均降雨量为1 265 mm，属于湿润地区。选取2000-2004年日平均流量用于模型率定，2005-2007年的资料用于模型验证。为了减轻初始条件对模型计算的影响，2000-2004年的前20%时间序列数据不用于模型率定过程(Warm up 设置20%)。模型的输入为根据流域内的气象站和降水遥测站根据泰森多边形计算的日面雨量数据，流域内马尔康和小金站的日气温观测数据，用于与模拟流量数据对比的是高场站2000-2007年的日流量数据。

2.2 模型

模型包括产流和汇流部分。产流部分用于将总降雨量转化为有效降雨量，汇流部分将有效降雨量转化为可与观测流量对比的流域出口断面流量。本研究采用Ye等人[17]提出的改进流域湿度损失方程计算产流,该模型是对Jakeman[18]提出的流域湿度指标模型的改进，汇流部分采用两个平行线性水库模型进行计算，改进后的模型具有更严格的统计意义，能被广泛应用于湿润地区的降雨径流计算，详见文献[17]。需要率定的模型参数为9个，包括6个产流模型参数(τ、pref、mf、l、p、Sin)及3个汇流模型参数(kq、ks、q)。表1给出了模型中9个参数的先验取值范围。以上参数范围的设置基于模型参数的物理意义并结合其在其它与研究区具有相似环境地区的应用经验，以及基于作者对岷江流域地区水文模型的多次计算分析所得出的较为合适的范围取值。模型的实现基于英国帝国理工学院土木与环境系自行研发的RRMT(Rainfall-Runoff Modelling Toolbox)[19]降雨径流模型工具包。

2.3 目标函数及似然值定义

采用如式(5)所示的Nash-Sutcliffe法作为本研究的目标函数，用于评价实测流量与计算流量的拟合程度。Nash-Sutcliffe法可以集合整个率定过程的残余误差，峰值流量对结果的贡献较大。NSE*越靠近零，拟合度越高。本研究全局敏感性分析基于式(6)所示的似然函数，该似然函数的定义没有严格意义上的统计依据，可被视为一种相对概率，用于表达参数组能描述现实水文系统的概率情况。式(6)中i表示第i次取样，N表示NSE*小于给定临界值的对应参数组个数。

(5)

(6)

表1 降雨径流概念模型参数取值及其物理意义

3 结果与讨论

3.1 基于SCEM-UA算法的参数优选分析

图1 比例缩小系数演化过程

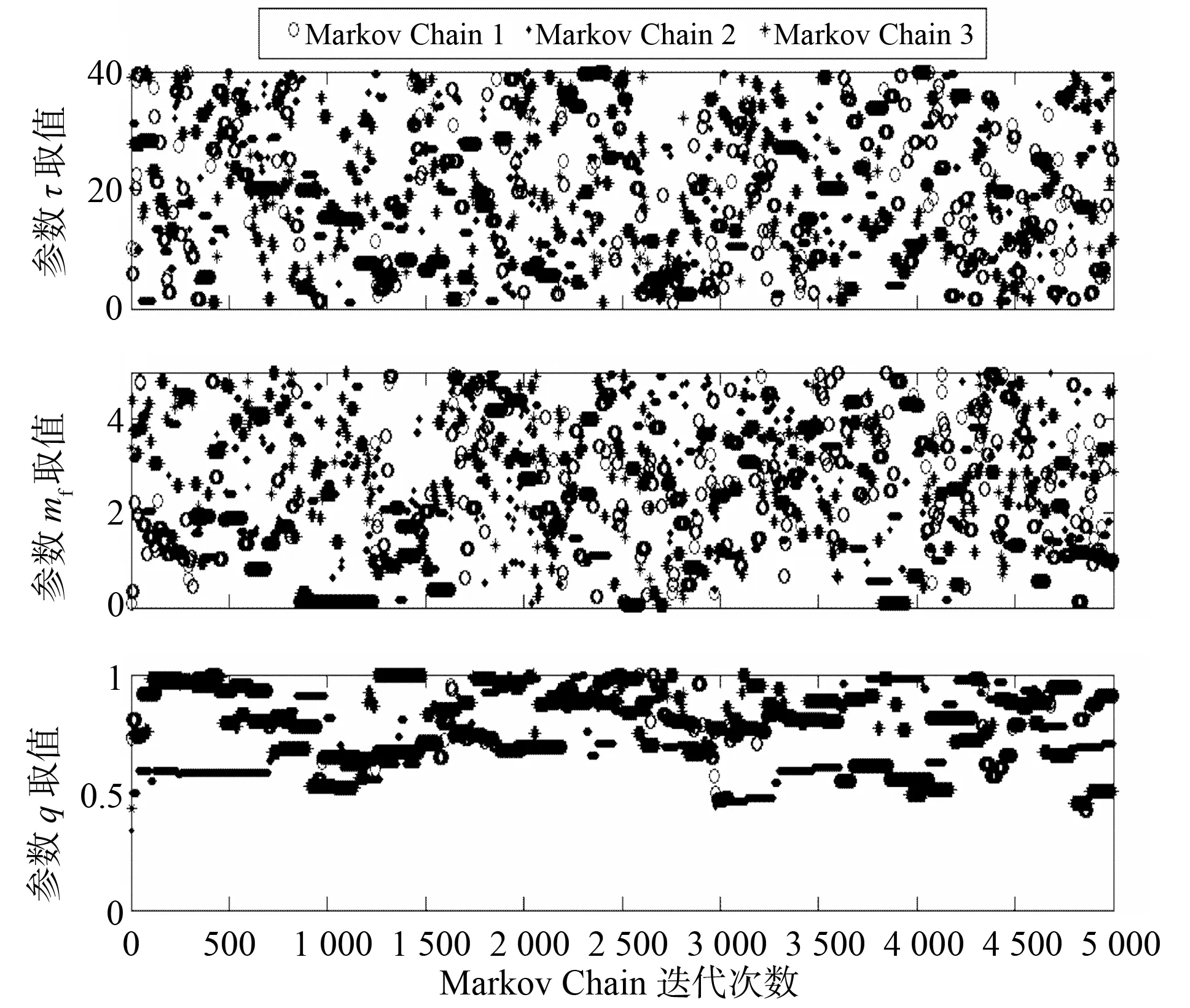
图2 参数τ和mf以及q对应的Markov链演化过程

图3 参数后验分布直方图

选取由SCEM-UA算法取样获得的对应NSE*小于临界值1的模型参数组，可得如图3所示的边缘后验概率分布。图3中每个参数的取值范围被等分成20个直方图，每个直方图所对应的概率根据式(2)或式(3)求得。从图中可知，参数l、p、kq、ks及q的后验分布成偏正态分布，其余4个参数的后验分布基本为不规则分布，但都具有峰值。这说明SCEM-UA算法能确保Markov链收敛于高概率后验分布区，从而使参数后验分布存在显著的峰值。

SCEM-UA算法取样获取30 000个样本，选取比例缩小系数小于1.2的样本，进行参数后验分布统计，结果如表2所示。表2 共统计了参数后验分布均值、标准差、最大值、最小值。SCEM-UA算法获得参数的后验分布而不是一组唯一的最优参数解，一般认为SCEM-UA算法的对应最优解应该位于最高后验概率分布区内，因此本文对比分析了SCEM-UA算法获得的参数最大后验概率对应参数值和SCE-UA算法获取的最佳参数值。表中的均值和SCEM-UA算法获得的参数最大后验概率对应参数值较为接近，说明参数分布是朝着高概率区进行收敛。表2中最大值和最小值基本和参数取值范围相一致，也说明了Markov链具有各态遍历性。SCEM-UA列和SCE-UA列对应的参数值有些很接近，相对误差较大的原因是由参数本身的辨识性不强决定的。

3.2 敏感性分析结果比较

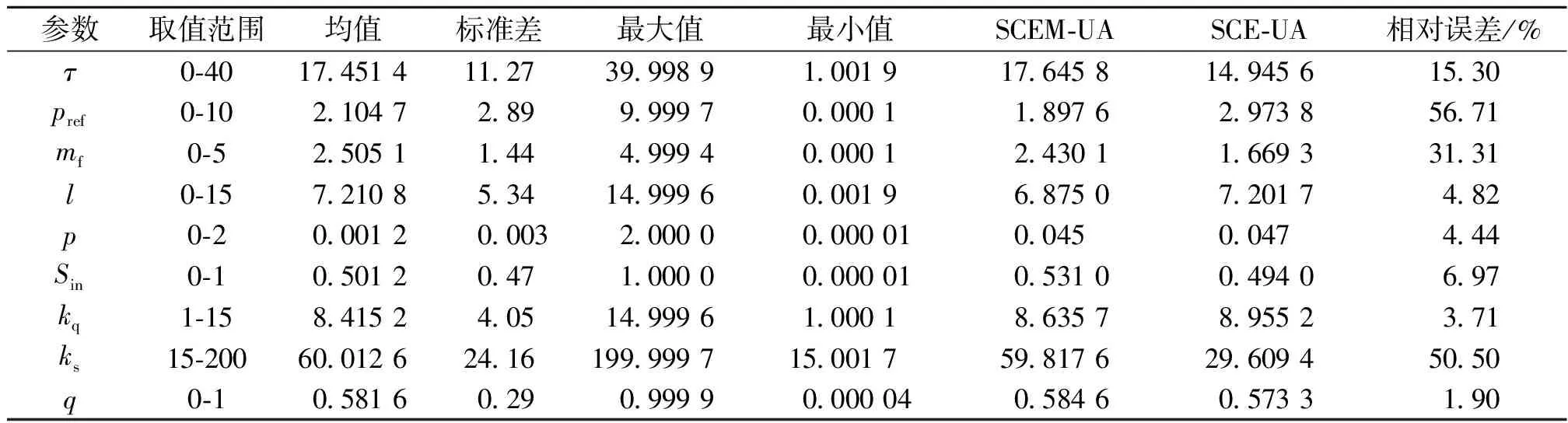
表2 参数后验分布统计情况1)

1)SCEM-UA列代表最大后验概率对应的参数取值，SCE-UA列代表由SCE-UA算法获取的最佳参数取值。

图4 全局敏感性分析图

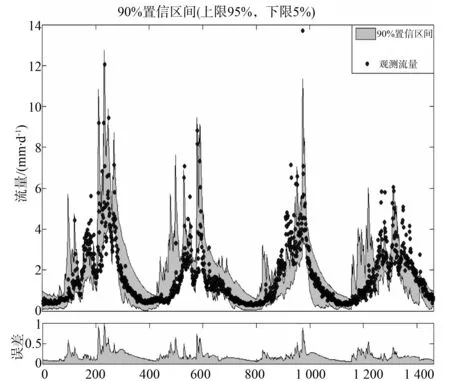
图5 模型率定过程下90%置信区间的计算值与观测值的拟合情况 (20000101-20041231，Warm up=20%)

图6 模型验证过程下90%置信区间的计算值与观测值的拟合情况 (20050101-20071231)

选取由SCEM-UA算法取样获得的NSE*小于临界值1的模型参数组，基于式(6)所定义的似然值可得到如图4所示的敏感性分析图。图4中参数组根据对应目标函数值从小到大等分成10组，每组根据式(6)计算对应的似然值，将似然值归一化后获得累积频率分布。图4紫色曲线对应似然度最高的边缘累积分布曲线，蓝色曲线代表似然度最低的边缘累积分布曲线，两曲线的水平距离相隔越远代表此参数敏感性越强，反之，敏感性越弱。由图5可知，流域蓄水量与有效降雨量之间的非线性相关系数p的敏感性最强，有效降雨量的临界值系数l的敏感性次之，其次为参数ks及q。对比分析图2-4可知，参数敏感性和后验分布情况密切相关，敏感性强的参数其Markov链在演化过程中收敛于范围较窄的高概率后验区，其边缘后验概率密度分布存在明显的峰值，相反，敏感性弱的参数对应的Markov链分布在较宽的区间内，其后验概率分布较为平坦且无规律可循，从而导致模型参数的不确定性大大增强。

3.3 模型输出不确定性分析

由SCEM-UA算法获取30 000个参数组，设置目标函数值临界值为1(NSE*)，小于临界值的对应参数组为8 764个，对8 764个参数组分别进行计算，每个步长(1 440 min)对应8 764个计算流量值，根据这些流量数据获取每个步长的流量分布情况，并设定置信区间为90%(置信度上限为95%，下限为5%)的模型计算不确定性区间。由图5和图6可知，置信区间为90%的计算结果基本较好地包含了观测值，根据误差情况来看，模拟精度较为良好，但整个率定、验证过程观测流量的峰值有跃出90%置信区间的情况，率定期第三个峰处、验证期第一及第三个峰处的拟合情况有待进一步提高，分析原因，模型结构本身和观测流量值(系统性偏差)存在的误差以及单目标函数的选取都会影响实测流量与计算流量的拟合结果。此外，流域上的许多人类活动影响也是造成上述现象的重要原因之一，例如流域中的水利工程设施(中小型水库、水土保持措施工程、跨流域调水工程等)，这些水利工程的规模影响流域产流参数和产流的整个过程，最终导致水文资料的不一致性。因此，系统科学的降雨-径流模型研究，还应该对这些水利工程的控制流域面积、蓄水能力、流域分布位置、建造时期、管理调度方式等情况进行详细研究。

4 结 论

1)本文以岷江流域作为研究实例，应用SCEM-UA算法和RSA方法分析了集总式降雨径流模型的参数后验分布及参数敏感性情况，对由于模型参数误差引起的模型输出不确定性进行了估计。结果发现，参数的强敏感性往往对应着参数边缘后验概率密度分布存在明显的峰值，相反，参数的弱敏感性使得后验概率分布较为平坦，也即参数的辨识性不强，从而导致参数选取的不确定性大大增强；

2)SCEM-UA算法的取样无需给定先验分布，更适用于参数先验信息较少的复杂水文模型参数后验分布的推算；

3)由参数后验分布统计可知，Markov链朝着高概率后验分布区进行收敛，且具有各态遍历性；

4)相比SCE-UA算法而言，SCEM-UA算法更侧重模型的不确定性分析，不仅可以搜索模型参数后验分布情况，而且可推求一定置信区间下的模型计算值与观测值的拟合情况，为模型参数及输出的不确定性分析奠定基础，并可指导模型结构的进一步优化。

参考文献：

[1]VRUGT J A, BOUTEN W, GUPTA H V, et al. Toward improved identifiability of hydrologic model parameters: The information content of experimental data [J]. Water Resources Research, 2002,38(12), 1312, doi: 10.1029/ 2001WR001118.

[2]MARSHALL L, NOTT D, SHARMA A. A comparative study of Markov chain Monte Carlo methods for conceptual rainfall-runoff modeling [J]. Water Resources Research, 2004, 40, w02501, doi:10.1029/2003WR002378.

[3]王建平， 程声通， 贾海峰. 基于MCMC法的水质模型参数不确定性研究[J].环境科学, 2006, 27(1):24-30.

[4]VRUGT J A, BRAAK J F, CLARK M P, et al. Treatment of input uncertainty in hydrologic modeling: Doing hydrology backward with Markov chain Monte Carlo simulation [J]. Water Resources Research, 2008, 44, W00B09, doi: 10.1029/2007WR006720.

[5]BLASONE R S, MADSEN H, ROSBJERG D. Uncertainty assessment of integrated distributed hydrological models using GLUE with Markov chain Monte Carlo sampling [J]. Journal of Hydrology, 2008,353：18-32.

[6]BLASONE R S, VRUGT J A, MADSEN H, et al. Generalized likelihood uncertainty estimation (GLUE) using adaptive Markov Chain Monte Carlo sampling [J].Advances in Water Resources, 2008,31(4): 630-648.

[7]DUAN Q Y, GUPTA V K, SOROOSHIAN S. Shuffled complex evolution approach for effective and efficient global minimization [J]. Journal of Optimization Theory and Application, 1993, 76(3): 501-521.

[8]BOYLE D P, GUPTA H V, SOROOSHIAN S. Toward improved calibration of hydrological models: Combing the strengths of manual and automatic methods [J]. Water Resources Research, 2000, 36(12): 3663-3674.

[9]马海波，董增川，张文明，等.SCE-UA算法在TOPMODEL参数优选中的应用[J]. 河海大学学报:自然科学版, 2006, 34(4): 361-365.

[10]VRUGT J A, GUPTA H V, BOUTEN W, et al.A shuffled complex evolution metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters [J].Water Resources Research, 2003, 39(8), 1201, doi:10.1029/2002WR001642.

[11]HAARIO H, SAKSMAN E, TAMMINEN J. An adaptive Metropolis algorithm [J]. Bernoulli, 2001, 7(2):223-242.

[12]HORNBERGER G, SPEAR R. An approach to the preliminary analysis of environmental systems [J]. Environmental Management, 1981,12(1):7-18.

[13]曹飞凤，许月萍，玄英姬，等.流域决策的不确定性分析[J].浙江大学学报：工学版，2009，43(1)：188-192.

[14]THIEMANN M, TROSSET M, GUPTA H, et al. Bayesian recursive parameter estimation for hydrological models [J]. Water Resources Research, 2001, 37 (10)：2521-2535.

[15]卫晓婧， 熊立华， 万民，等. 融合Markov链-蒙特卡洛算法的改进通用似然不确定性估计估计方法在流域水文模型中的应用[J]. 水利学报, 2009, 40(4):464-480.

[16]GELMAN A, RUBIN D B. Inference from iterative simulation using multiple sequences [J].Statistic Science, 1992(7):457-472.

[17]YE W, BATES B C, VINEY N R, et al. Performance of conceptual rainfall-runoff models in low-yielding ephemeral catchments [J]. Water Resources Research, 1997, 33(1):153-166.

[18]JAKEMAN A J, HORNBERGER G M. How much complexity is warranted in a rainfall-runoff model? [J]. Water Resources Research, 1993, 29(8): 2637-2649.

[19]WAGENER T, LEES M J. Rainfall-Runoff Modelling Toolbox user manual [R]. UK: Department of Civil and Environmental Engineering, Imperial College London, 2001.

[20]WAGENER T, KOLLAT J. Numerical and visual evaluation of hydrological and environmental models using the Monte Carlo analysis toolbox [J]. Environmental Modeling and Software, 2007,22:1021-1033.