求解大规模线性时不变系统的最优2模型降阶问题的共轭梯度法*

曾泰山，鲁春元，陈 剑

(1.中山大学数学与计算科学学院，广东 广州 510275；2.广东药学院医药信息工程学院，广东 广州510006;3.佛山科学技术学院数学系，广东 佛山528000)

近年来，模型降阶越来越受到重视。它可以大大降低大规模系统模拟和控制中的时间复杂度，在超大规模集成电路设计，实时控制，天气预报等领域有着重要应用。关于模型降阶的综述，参见文献[1-2]。

给定矩阵A∈Rn×n，B∈Rn×p和C∈Rq×n，线性时不变系统可以表示成：

(1)

y(t)=Cx(t)

(2)

其中t≥0表示时间变量，u(t)∈Rp表示输入，y(t)∈Rq表示输出，x(t)∈Rn表示系统的状态。n是系统的阶。p和q是系统的输入和输出个数。当系统的阶n很大的时候，由于需要大规模计算和存储，这使得系统的数值模拟和控制非常困难。解决这一问题的一种关键方法是构造一个低阶的系统去逼近原始的高阶系统，并保持相应的系统特性。

(3)

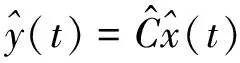
(4)

定义全阶系统(A,B,C)的传递函数为

G(s)=C(sI-A)-1B,s∈C

方程 (3) 和 (4) 描述的降阶系统的传递函数为

CU(sI-UTAU)-1UTB,s∈C

(5)

CU(sI-UTAU)-1UTB

(6)

定义代价函数

(7)

(8)

[U]:={UQm|Qm∈Om}

其中,Om表示所有m×m正交矩阵构成的正交群，U∈Rn×m满足UTU=I。由定义可知，等价类[U]中的矩阵的列向量张成的线性子空间相同。 在实际计算中，我们将选择其中一个正交矩阵U∈Rn×m来代表整个等价类。关于Grassmann流形的几何性质，参看文献 [10-11]。

由方程 (6) 以及代价函数J(U)的定义 (7)可以看出

J(U)=J(UQm),∀Qm∈Om

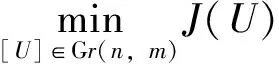
(9)

通过利用 Grassmann 流形的几何性质，我们将提出求解问题 (9) 的数值算法。

在 (6) 定义的误差传递函数Ge(s)可改写为

Ge(s)=Ce(sI-Ae)-1Be,s∈C

实际上，矩阵Ae，Be和Ce定义了一个系统实现为(Ae,Be,Ce)的误差系统。Ge称为是误差系统的传递函数。误差系统的可控性Gramian矩阵Ec和可观测性Gramian矩阵Eo由如下的Lyapunov方程所定义

(10)

(11)

我们将可控性Gramian矩阵Ec和可观测性Gramian矩阵Eo做如下分划

∑c,∑o∈Rn×n,P,Q∈Rm×m

Lyapunov方程 (10) 和 (11) 可以转化为

A∑c+∑cAT+BBT=0

(12)

AT∑o+∑oA+CTC=0

(13)

UTAUP+PUTATU+UTBBTU=0

(14)

UTATUQ+QUTAU+UTCTCU=0

(15)

AX+XUTATU+BBTU=0

(16)

ATY+YUTAU-CTCU=0

(17)

代价函数J(U)可以用Gramian矩阵Ec表示如下[9]

trace[CTC(∑c+UPUT-2XUT)]

(18)

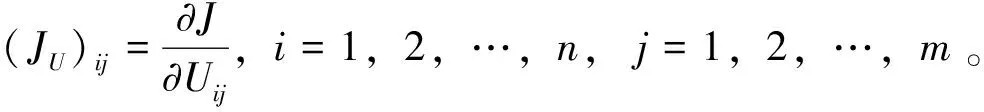
R:=AT[U(YTX+QP)]+A[U(XTY+PQ)]+

CT[C(-X+UP)]+B[BT(Y+UQ)]

(19)

代价函数J(U)在点U的偏导数为

JU=2R

由参考文献 [11]， 在点[U]∈Gr(n,m)处的切空间T[U]Gr(n,m)可以表示为

T[U]Gr(n,m)={ξ∈Rn×m|UTξ=0}

代价函数J的梯度▽J∈T[U]Gr(n,m)为

▽J=R-UUTR

(20)

2 共轭梯度法

下面我们给出共轭梯度算法的概要。假设 (A,B,C) 是全阶系统的状态空间实现。记Uk为第k步获得的模型降阶投影矩阵，k=0,1,…。在共轭梯度算法中，通过以Uk为起点，以Fk为方向的测地线上搜索得到下一个投影矩阵Uk+1。流形上的测地线流形上两点最短路径。以Uk为起点，方向为Fk的Grassmann流形的测地线为

(21)

(22)

为了计算下一步的搜索方向Fk+1，首先计算在点Uk+1处的梯度Gk+1=▽J(Uk+1)。通过求解以下的Sylvester方程来计算矩阵Pk+1，Qk+1，Xk+1和Yk+1，

(23)

(24)

(25)

(26)

矩阵Rk+1为

(27)

在点Uk+1偏导数JUk+1为JUk+1=2Rk+1。代价函数J在点[Uk+1]∈Gr(n,m)的梯度为

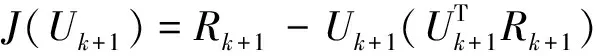
下面将介绍共轭梯度法的搜索方向构造。计算旧搜索方向Fk的平行移动

选取新的搜索方向为共轭梯度方向，即旧搜索方向的平行移动和新的梯度的线性组合

Fk+1=-Gk+1+γkτFk

(28)

在式子 (28)中，τFk为切向量Fk的沿着测地线的平行移动。切向量在流形上的平行移动是欧氏空间中向量平移的推广。类似于欧氏空间中共轭梯度法，组合系数γk可以通过下面的式子(Polak-Ribiere法则)得到

γk=/

(29)

其中τGk是梯度Gk的平行移动

τGk=Gk-(UkVksin(tkΛk)+

值得指出的是，如果令γk=0，则Fk+1=-Gk+1，即搜索方向为负梯度方向，此时共轭梯度法就退化为文献[7]中的梯度流算法。

下面是本文提出的共轭梯度法(CGA)的主要框架。

Algorithm 1: 共轭梯度法(CGA)

2)Fork=0,1,2,…,N-1

b)求解极小化问题

(30)

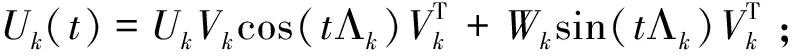
c)计算梯度Gk+1=▽J(Uk+1)；

d)平行移动切向量Fk和Gk到点 [Uk+1]:

计算新的搜索方向

其中

Endfor

3) 获得投影矩阵U=UN，计算

在上述算法中，需要求解极小化问(30)，这可以通过不完全线性搜索算法来求得，例如Armijo 搜索方法，可参见文献 [10]。

对于Grassmann 流形上的最优化问题，共轭梯度法在满足一定的条件下达到超线性收敛[10-11]。因此，本文提出的共轭梯度算法也能达到超线性收敛。

另外，由于本文所提出的共轭梯度算法不需要求解大规模的 Lyapunov 方程，因此计算量大大减少。下面，我们来分析共轭梯度算法的计算复杂性。在本文中，将以乘法次数来衡量计算复杂性。记Ns极小化问题 (30) 的最大搜索步数。记N为最大迭代次数。

定理1 假设A∈Rn×n是个具有N(A)个非零元素的稀疏矩阵。假设存在一个只需要O(rn+N(A))次乘法运算的线性方程求解方法求解方程

(A-ηI)x=b,η∉σ(A),b∈Rn

(31)

其中r是个固定的整数。则共轭梯度法CGA计算复杂度为

O(N(nmr+mN(A)+Nsnm2+nmp+nmq))

证明 在第k步迭代中，k=0,1,…，算法 CGA 的计算花费主要来自以下三个方面：

第一部分是Pk、Qk、Xk和Yk的计算，需要求解Sylvester方程 (23)-(26)。在文献[7]中指出，如果存在一个只需要O(rn+N(A))次乘法运算的方法求解方程 (31)，则利用文献[12]中的方法求解 Sylvester 方程 (23)-(26) 的计算复杂度只需

O(nmp+nmq+nmr+mN(A)+m3)

第二部分是搜索方向Fk的计算。对给定的A，B，C和Uk，需要O(mN(A)+nm2+nmp+nmq)次乘法运算来计算Rk。因此，它需要O(mN(A)+nm2+nmp+nmq)次乘法运算来计算Fk。

第三部分是非精确搜索方法求解最小化问题 (30) 以获得步长tmin。对极小化问题 (30) 的每一个搜索步，我们需要计算测地线方程 (21)。易知，测地线的计算复杂度为O(nm2)。 因为最大的搜索步数为Ns，所以非精确搜索方法求解最小化问题 (30) 的计算复杂度为O(Nsnm2)。

总而言之，算法CGA每一步迭代需要O(nmr+mN(A)+Nsnm2+nmp+nmq) 次乘法次数。由于算法CGA的最大迭代次数为N，因此算法的总的复杂度为

O(N(nmr+mN(A)+Nsnm2+nmp+nmq))

如果降阶系统的阶m远远小于原始大规模系统的阶n，且系统的输入输出个数p和q也远远小于n，此时共轭梯度法的计算复杂度为线性O(Nn)，其中N为迭代次数。

3 数值算例

在本节，我们测试比较了本文提出的共轭梯度法的有效性。

例1 考虑在区域Ω=(0,1)2上的热传导方程。热传导方程可以有如下形式

其中u=u(t,x,y)，(x,y)∈Ω，t∈[0,∞)。假设微分方程在空间域上等距剖分，格点数为d×d。导出的刚度矩阵A∈Rd2×d2是稀疏的、稳定的，带宽为d。系统的阶为n=d2。假设b1∈Rn是一个所有元素都为1的向量。b2∈Rn是个随机向量。假设B=[b1,b2]，C=BT。 此时，构造的系统 (A,B,C) 是个多输入多输出系统。

表1 2相对误差比较

图1 收敛曲线比较

4 总 结

参考文献：

[1]ANTOULAS A C. Approximation of large-scale dynamical systems [M]. Adv Des Control 6 SIAM, Philadelphia, 2005.

[2]GUGERCIN S, ANTOULAS A C. A survey of model reduction by balanced truncation and some new results [J]. International Journal of Control, 2004, 77(8): 748-766.

[3]HUANG X X, YAN W Y, TEO K. Linear-optimal model reduction [J]. IEEE Trans Automat Contr, 2001, 46: 1279-1284.

[4]HYLAND D C, BERNSTEIN D S. The optimal projection equations for model reduction and the relationships among the methods of wilson, skelton and moore [J]. IEEE Trans Automat Contr, 1985, 30: 1201-1211.

[5]LEPSCHY A, MIAN G A, PINATO G, et al. Rational approximation: a non-gradient algorithm [C]//Proc 30th IEEE CDC, 1991: 2321-2323.

[6]YAN W Y, LAM J. An approximate approach to optimal model reduction [J]. IEEE Trans Automat Contr, 1999, 44: 1341-1358.

[9]ZHOU K, DOYLE J C, GLOVER K. Robust and optimal control [M]. New Jersey: Prentice-Hall, 1996.

[10]ABSIL P A, MAHONY R, SEPULCHRE R. Optimization algorithms on matrix manifolds [M]. Princeton University Press, 2008.

[11]EDELMAN A, ARIAS T A, SMITHS T. The geometry of algorithms with orthogonality constraints [J]. SIAM J Matrix Anal Appl, 1999, 20: 303-353.

[12]VASILYEV D, WHITE J. A more reliable reduction algorithm for behavior model extraction [C]// Proc Int Conf on Computer， Aided Design (ICCAD), 2005: 812-819.