对一道能量类连接体问题的深入探讨

李中玉 李小洪

（佛山市南海中学 广东 佛山 528211）

笔者在教学中遇到这样一道题目，该题也常见于其他参考资料，其似是而非的解答，对教师和学生都有不良影响.笔者将其整理如下.

【原题】如图1所示，质量为2m和m的可看作质点的小球A和B，用不计质量、不可伸长的细线相连，跨在固定光滑圆柱两侧，圆柱截面圆半径为R.开始时，A球和B球与圆柱轴心同高，然后释放A球.求：B球在圆柱上最高点时的速率.

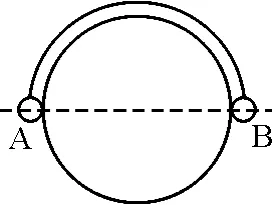
图1

原题解析：A和B两球组成系统机械能守恒，所以

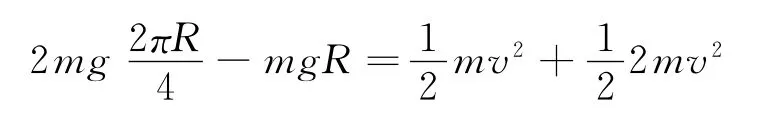
所以B球在圆柱上最高点时速率

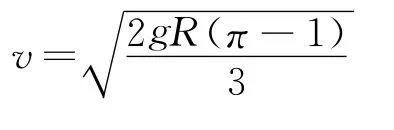
图2

设B球和圆柱截面圆心连线与水平方向夹角为θ时，B球与圆柱间弹力为零.此时对B球受力分析，如图2所示.由向心力公式得

从释放A球到B球刚要脱离圆柱时，A和B球组成的系统机械能守恒，故

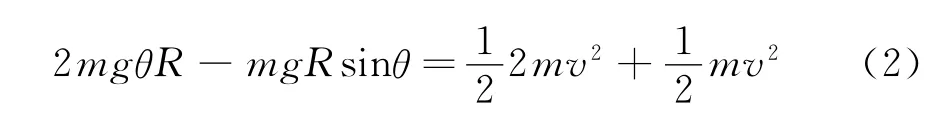
由（1）、（2）式联立，得

这是一个超越方程，要中学生求解，非常难.但对于一个出题者来说却是不可或缺的.笔者在这里先用作图法，再用半分插值法求解.

1 粗略分析

用Excel从θ为零开始每增加描一个点，在同一坐标图中，分别作方程y＝4θ和y＝5sinθ的图像（图3），它们交点的横坐标就是方程（3）的解.

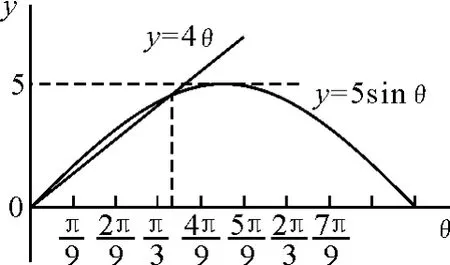
图3

从图3可看出方程（3）有两个解.一个是θ＝0，另一个在之间.这两个解都小于，故原解析不正确.可是，仅这样分析并不能解出最终结果.应怎样才能解出B球在圆柱上最高点时的速率呢？

2 用半分插值法精确求解

为求出最终结果，笔者采用了半分插值法.该操作，依然在Execl中进行，其思路如下.

（2）半分插值.求得θ在之间的中间值以及该中间值对应的4θ－5sinθ值.

（3）确定新的两端数值.比较θ为中间值时4θ－5sinθ值，与时哪一个4θ－5sinθ值正负号相反，将该θ值与中间值作为下次插值端点数值.因值正负号相反，故为下次插值两端数值.

（4）以新两端数值进行半分插值，至所需精度内4θ－5sinθ值等于零为止.笔者将该值精确到了小数点后两位，如表1所示.

表1 θ不同时4θ－5sinθ值

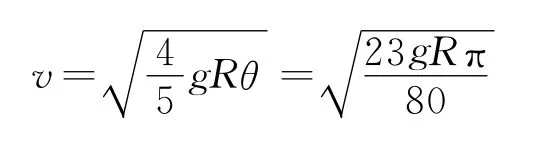
至此，我们已较为精确地解出了最终结果.对类似问题的求解，也当如此.

半分插值法尽管对所有该类问题都能求解，但B球能到达圆柱圆截面顶点时，依然用该办法求解，就显得繁琐了.因此，进一步探讨B球上升至圆截面顶点的条件，将为解答此类问题带来便捷.

3 B球能达到圆截面顶点的条件

B球能上升是由A，B两球质量不同引起的.A，B两球质量之比为何值时，B球才能到达圆柱圆截面顶点呢？

为此，不妨设A球质量是B球质量m的n倍，即nm，令带入方程（1）、（2）中求解，此时可解得即A球质量为B球的倍时，B球可到达圆柱圆截面顶点，且恰好对圆柱无挤压.

根据能量转化的关系可知，若n则B球在到达圆柱圆截面顶点前已脱离圆柱；若n＜则B球上升至圆柱圆截面顶点时，对圆柱有挤压.要让B球上升，A球的质量不能小于B球的质量.故B球能上升至顶点，A，B两球质量之比n的范围为

而原题中的n＝2，显然不在此范围.

这样，在今后遇到该类问题时，我们便能确定其求解方法.若A，B两球质量之比n范围为n＞1，B球能到达圆截面顶点，采用原解析思路.若n取值范围大于B球不能上升至圆截面顶点，采用半分插值法.若n取值范围小于1，则A球上升，其思路与B球上升时完全相同.

由此可见，出题和解题都不能想当然.只有实事求是地给予判断和多方面考察，方能确定题目的真实性、实用性和求解的正确性；否则会给学生物理思维的发展带来误导，从而违背物理学精神.