加筋结构动力特性和动力响应分析
赵望胜 刘 澔 叶建新
在土木工程中,由于基体材料的性能不足,大量使用各种加筋材料来增强和改善结构的力学性能。加筋结构中加筋材料与基本材料作用方式复杂,选择合理的有限元模型便于模拟加筋构件布置的情况,可以很好的模拟加筋构件与基本材料之间相互作用情况,实现对加筋结构进行动力特性和动力响应分析。
目前,在实际过程中,总伴有不同类型的阻尼力,产生这种阻尼力的因素可归结为两个方面:1)外部介质的摩擦阻尼力;2)结构内部变形时的内耗。由于材料结构组成复杂,导致阻尼力性质很复杂,这类振动力学计算尚没有很好的解决。
1 动力学的精细积分算法
一般而言,确定线性系统的动力方程可写为:
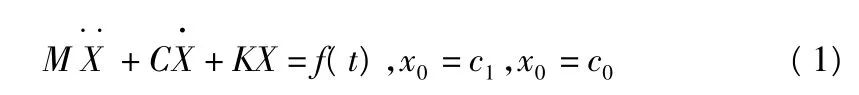
其中,M,C,K分别为质量矩阵、阻尼矩阵、刚度矩阵;f(t)代表激励,假设自由度为n,将式(1)写成状态方程:
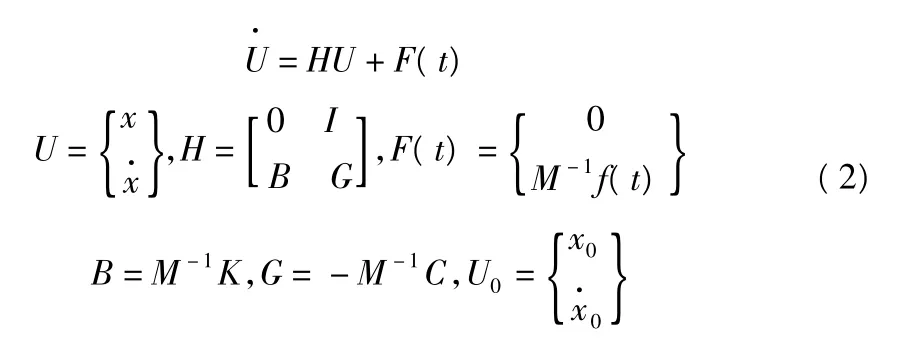
对式(2),它的解可写成如下形式:

对式(3)进行数值离散,并假设时间步长Δt=tk+1-tk,则第k+1步时的响应公式可写为:
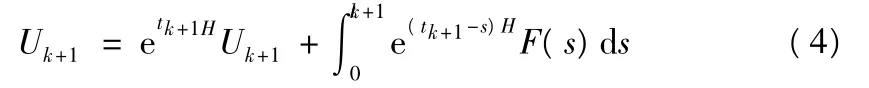
对式(4)可作如下变形:

在式(5)中,T=exp(ΔtH),它可用数值方法精细计算而得。为使式(5)也能直接进行数值计算,可用数值积分方法将其式中的第二项算出。在这里,选用格式较为简单同时精度又较高的辛普森积分法,也即:

其中,Tt=exp m(0.5ΔtH),所以式(4)可变为:

式(7)即是计算系统响应的迭代公式。
2 模型
加筋构件静力学算例问题,如图1所示。混凝土一端固定,另一端一节点处受有集中力作用,混凝土的弹性模量E=2.0e10、密度 ρ=2 400 kg/m3、泊松比 v=0.3,钢筋弹性模量 E=2.0e11、密度 ρ=9 000 kg/m3、截面面积 0.08 m2、泊松比 v=0.3。集中力F=1.0e4。
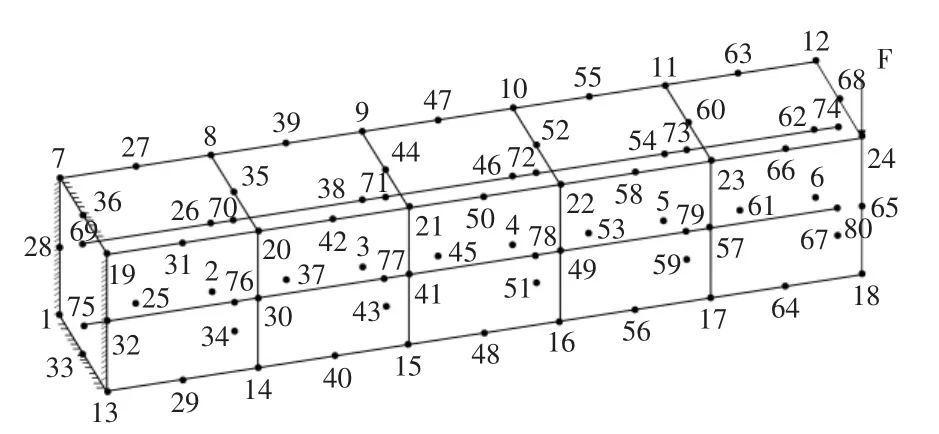
图1 加筋结构示意图

图2 加筋结构的无阻尼自由振动

图3 无钢筋结构的无阻尼自由振动
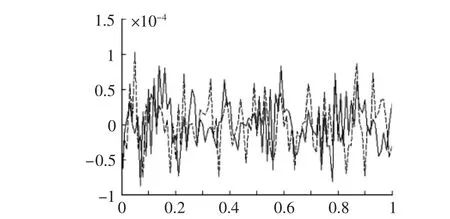
图4 无钢筋结构和加筋结构的无阻尼自由振动比较
3 模型结果和分析
针对如图1所示的模型,在这里为了表示结构自由振动模型的准确性,选取加筋结构在荷载作用下的位移作为结构自由振动的初始位移,而速度假设为0。可以理解为加筋结构受到静力荷载后突然释放的自由振动,这种情况更适合实际情况。阻尼C=1.0e-2M+2.0e-4K(M,K分别为结构的质量阵和刚度阵)。图2,图3是加筋结构和不考虑加筋结构在初始位移激励下的无阻尼自由振动,图4是考虑钢筋和不考虑钢筋结构的无阻尼自由振动对比示意图。
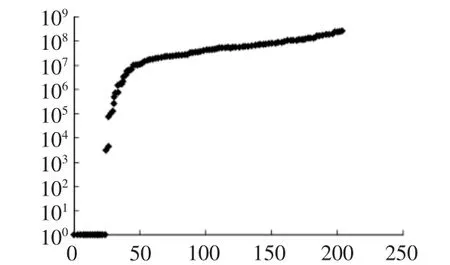
图5 加筋结构的固有频率对数曲线
从图4可以看出,加了钢筋后,结构抵抗振动的能力变强,也说明钢筋对整个结构的固有频率有增大的作用。为了更直观的说明这个问题,在求解出结构(加筋和非加筋结构)的质量阵和刚度阵之后,就可以得到其固有频率,如图5,图6所示。

图6 无筋结构的固有频率对数曲线
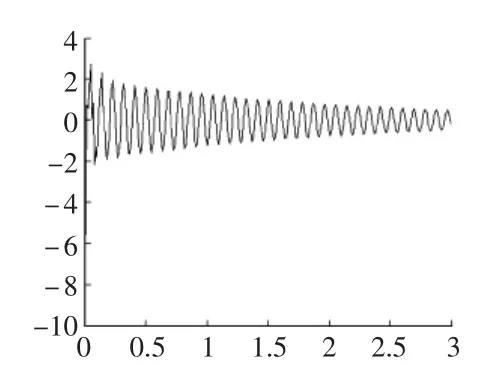
图7 加筋结构有阻尼自由振动
表1是得到结构的刚度阵和质量阵后,求解出来的结构的部分自振频率。从表1的频率对比可以看出,加筋结构的自振频率比无筋结构的自振频率要大,这也说明了钢筋对结构有刚度贡献,从而提高了结构的自振频率。图7是有阻尼的自由振动结构的示意图,从图7可以看出位移有规律的逐渐衰减,这正是所期待的结果。

表1 加筋和无筋结构的固有频率比较
4 结语
状态方程直接积分法不仅用于求解在线性激励、简谐激励作用下系统的动力响应,还可以求解在一般荷载作用下系统的动力响应;不仅可以用于求解线性系统的动力响应,还可以用于求解非线性系统动力的响应计算,且精度高,速度快。
为有阻尼和无阻尼结构振动计算分析带来极大的方便,进而解决加筋结构中加筋的布置,从而为提高结构稳定性分析研究做出了理论计算分析价值。算例就是很好表明了加筋后结构的稳定性明显提高。
[1] 尹晓芷,刘彦昌.钢筋混凝土梁动力特性检测研究[J].山西建筑,2009,35(4):104-105.
[2] 夏樟华,宗周红.预应力对混凝土梁动力特性的影响分析[J].振动与冲击,2007,26(7):129-134.
[3] 杜金龙,郭少华.钢筋混凝土损伤梁动力特性的有限元分析[J].石家庄铁道学院,2007,20(3):18-23.
[4] 钟万勰.暂态历程的精细计算方法[J].计算结构力学及其应用,1995,12(1):1-6.
[5] 钟万勰.矩阵黎卡提方程的精细积分[J].计算结构力学及其应用,1994,11(2):113-119.
[6] 张森文,曹开彬.计算结构动力响应的状态方程直接积分法[J].计算力学学报,2000(2):95-96.
[7] 张相庭.结构振动力学[M].上海:同济大学出版社,2005.

