BP 神经网络在路面材料抗压强度预测中的应用
孙延成
0 引言
近年来,神经网络在预测实验数据等方面得到了广泛的应用。神经网络的信息处理系统,是通过对连续的或者间断式的输入作状态响应而进行信息处理。它由彼此之间高度连接排列成层的神经单元组成,这些单元是模仿大脑中的神经细胞设计而成[1]。接收输入信号的单元层称为输入层,输出信号的单元层称为输出层,不直接与输入和输出发生联系的单元层为中间层或隐层。每个处理单元都有3个基本功能,即接收输入,对输入进行处理,计算输出。神经网络的处理功能都是由这些简单的处理单元完成的,各处理单元之间通过权值连接,单元的所有这些连接决定了该神经元的连接模式,该连接模式可以用一个权值矩阵来表示,这些连接可以传递信号,每个单元都从它的输入连接接收许多信号,这些输入信号来自别的单元或边界,每一个单元有一个信号输出。输出信号通过单元间的连接传递到其他单元,输出的每个单元都传递相同的输入信号[2]。
1 试验数据处理与隐层结构的选取
1.1 输入量与输出量的设计
在确定网络输入变量时考虑试件均在重型击实条件,并在最佳含水量下成型,温度和湿度都在标准的条件下进行养护,并取7 d龄期的试件进行神经网络预测。本文将无侧限抗压强度作为网络输出,将基本材料水泥、碎石、风积砂等的基本参数数据作为网络输入变量。目标向量就是通过试验测得的试件无侧限抗压强度,这样一来,输出变量就成为一个一维的向量,提高了预测的精度,并减少了计算的时间。
在获得输入和输出向量后,为了减少计算中的相对误差,本文采用归一化处理,将数据处理为区间为[0,1]之间的数据。归一方法有很多种形式,这里采用如下公式:

输入向量与归一后数据如表1所示。
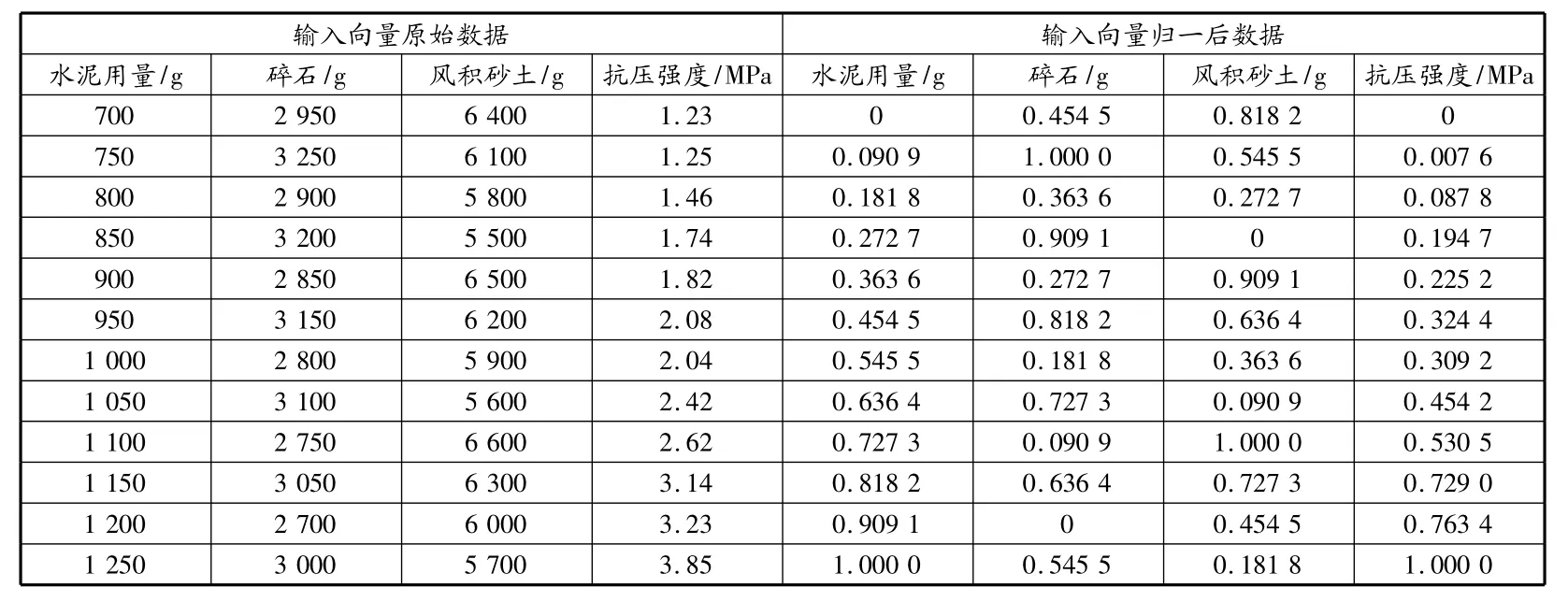
表1 输入向量原始数据与归一后数据
1.2 隐含层内节点数的选择
在BP神经网络算法中各层节点数的选择对网络的预测性能影响很大,所以隐含层内的节点数量需要进行合适的选择,一个多层网络需要多少隐含单元层,每层需要多少个节点,这些都是由网络的训练和性质来决定的(见表2)。因此,确定隐含层节点是一个复杂而十分重要的问题。
本文确定节点数所采用的公式为:

其中,m为输出神经元数;n为输入神经元数;a为1~10之间的常数。
本文采用单隐层的神经网络,而中间层的神经元个数需要通过计算机大量的试验来确定是由于单隐层BP网络的非线性映射能力比较强,由于输入神经元有3个,当隐层结构节点数取得小时,计算容易不收敛,导致误差偏差很大,因此,这里为中间层神经元个数选择3个值,分别为8,10和12,并分别检查网络性能。

表2 训练参数
隐含层数目的多少并不代表计算准确度的高度,隐层个数越高,计算的精度就越大,但是并不是预测的越准确,这也取决于网络的结构。不同个数隐单层组成的BP网络训练曲线分别如图1~图3所示,通过比较,中间层神经元个数为10时,网络的收敛速度最快。所以网络的结构为3×10×1。

图1 节点数为8时训练误差曲线
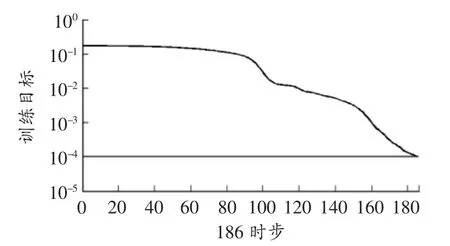
图2 节点数为10时训练误差曲线

图3 节点数为12时训练误差曲线
预测误差曲线如图4所示,由图4可见,在隐层结构取10节点时,网络的预测值和真实值之间的误差是非常小的,误差都在0.000 1左右。即使是最大的误差也只有0.015,这完全满足应用的要求。这也说明了在隐层结构增加的情况下,虽然带来了精度的增加,但是误差却没有相应的减小,同时也说明了隐层节点取合适的节点才能得到更加准确的结果。

图4 各结构层个数训练误差曲线
2 训练与预测结果
通过对表1数据进行系统的归一后将数据作为样本进行训练,并根据现有的数据对样本其本身进行预测,以此来检验其精度与可靠度。从12组试验中抽取10组数据作为样本,对网络进行学习训练,其余两组数据作为检验样本,用于检验网络的精度及推广能力。
通过图5的拟合曲线可以看出,实测值与神经网络预测模型的预测值非常吻合,说明该网络模型预测的精度很高。在现场施工与室内的实验过程中,混凝土试件需要长时间的养生,周期较长,并且数量较多,工作量很大,实验的检验结果相对施工相对滞后,不利于施工技术员及时发现问题并降低工程成本。因此,采用BP网络模型来预测路面基层稳定土的强度具有十分重要的意义。

图5 实测值与预测值拟合曲线
3 结语
1)从实验分析中可以得出,影响稳定土强度的因素比较多,在神经网络预测中,对这些影响因素进行相应的取值,便可作为输入变量输入到神经网络系统中,而且输入变量的数目多少对预测结果的影响很小;
2)采用人工神经网络模型对路面基层稳定土抗压强度进行预测,为了减小系统中训练样本所产生的误差,可以适当将目标误差调小,这种方法会加大预测样本的相对误差,会导致网络目标训练过多,致使网络的智能化搜索和推进能力下降,所以要选择能使训练和预测误差同时达到满意结果的目标误差值作为训练参数;
3)BP人工神经网络应用到试验数据的预测中,通过建立材料组成的配比关系与无侧限抗压强度间的神经网络模型,经过训练和仿真,并与已知数据进行对比分析,可知神经网络预测具有较高的精度,能够满足工程建设的需求,通过神经系统的预测分析,能对试件的无侧限抗压强度进行预测分析,这使施工技术员或监理工程师在质量控制中进行控制具有一定的实用价值,对工程具有一定的指导意义。
[1] 袁曾任.人工神经元网络及其应用[M].北京:清华大学出版社,1999:1-84.
[2] 吕砚山,赵正琦.BP神经网络的优化及应用研究[J].北京化工大学学报,2001,28(1):67-69.
[3] 丛 爽.面向MATLAB工具箱的神经网络理论与应用[M].北京:中国科学技术大学出版社,1998.
[4] 任瑞波,钟垈辉,张学慧,等.BP神经元网络在路基路面结构设计中的应用[J].东北公路,2003,26(2):19-20.
[5] 徐培华,王安玲.公路工程混合料配合比设计与试验技术手册[M].北京:人民交通出版社,2001.
[6] 杨文山.路面状况指数的BP网络预测[J].哈尔滨建筑大学学报,2007,33(3):108-110.
[7] 飞思科技产品研发中心.MATLAB7.0辅助神经网络分析与设计[M].北京:电子工业出版社,2006.

