尺寸误差对转子系统摩擦功率的因子分析研究
魏 塬,徐武彬,李 琳,曾海景
(1.广西工学院 机械工程系,柳州 545006;2.广西工学院 管理系,柳州 545006)
0 引言
随着科学技术及经济的发展,对旋转机械在速度、容量、效率和安全可靠性等方面提出了新的要求。旋转机械转子系统中存在许多非线性激励源的存在,须用非线性动力学理论来进行分析。系统而定量地研究尺寸制造误差对滑动轴承转子系统动力学特性的影响,研究考虑制造误差时系统非线性动力学分析、建模和计算方法,能为滑动轴承转子系统参数及其公差设计提供理论依据,使其对系统运行的影响在控制制造误差影响最小的区域内,对滑动轴承转子系统设计具有重要的理论和实际意义,为旋转机械的非线性动力学设计提供可靠的理论基础[1]。
国内外学者研究表明制造误差对系统的稳态和动态性能将产生重要影响[2~4],然而,目前进行的一些工作还不够深入,只是从宏观上分析了加工误差的影响,从微观角度分析尺寸误差的研究并不多。在实际的滑动轴承转子系统中,制造误差是不可避免的,在设计阶段应在允许的制造误差范围内合理的选择尺寸以尽量减少制造误差的影响,以确保系统在一个较稳定的范围内运行。滑动轴承转子系统的制造误差主要包括轴承的宽度误差、轴承和轴颈的直径误差以及运行时润滑油的温度变化对粘度的影响。虽然轴颈和轴承的尺寸制造误差与其绝对尺寸相比很小,但这些误差的影响是不容忽视的,现有的文献资料普遍认为它是轴承设计的关键。
本文介绍一种2k因子分析方法,用来验证各种不同的尺寸误差的滑动轴承支撑的旋转机械的稳态和动态特性及其能量损失的影响,并对计算结果进行相应的分析。考虑各参数对转子-轴承系统运行的偏差问题,可以知道哪些参数在设计、制造时需要严格控制,从而避免盲目设计,降低能量损耗,提高工作可靠性。
1 滑动轴承转子系统模型
图1(a)为径向滑动轴承转子系统的动力学模型[5],其中Oj为轴颈轴心,Ob为轴承轴心,dj为轴颈直径,db为轴承直径,h为油膜厚度,μ为流体动力粘度,N为转速,e为偏心距,Ф为转子处于稳定状态时的姿态角,θ为转子的位置角,Fbu、Fbv为油膜力在沿U、V方向的分量,Vt为轴颈切向速度。系统结构如图1(b)所示,主要包括电机、滑动轴承、转子、油管、电涡流传感器、配重块和基座等装置,包含了动力系统、供油系统、实验平台和检测系统4个部分。

图1 滑动轴承动力学系统
2 试验方案与设计
首先选用2k因子设计安排试验方案[6],本文考虑4个因子:动力粘度μ(A),轴承宽度L(B),轴承直径db(C)和轴颈的直径dj(D),其制造误差可用上偏差和下偏差表示。每个因子取2个水平,用“+”和“- ”符号来表示因子水平的高与低,小写字母l, a, b, c, d, ab, ac, …, abcd来代表24个组合,考虑这4个因子及交互作用都系统的影响。这些参数的任何变化都会改变Sommerfeld数的大小,进而影响稳定性和系统的动态特性。
为消除随机误差的影响,各试验方案采用随机化方式决定试验次序。2k因子设计的试验因素水平如表1所示,试验值的第2行所选独立因素为高水平,第3行所选独立因素为低水平。
因此,安排两组实验的16个观测计划表来评估这些因素的影响,如表2所示。第2列至第5列的“+”和“ - ”表示在一个标准的因子顺序A,B,C,D高、低级别的不同组合,并在后面四列给出因子的相应值。第6列是标准秩序的观测向量。
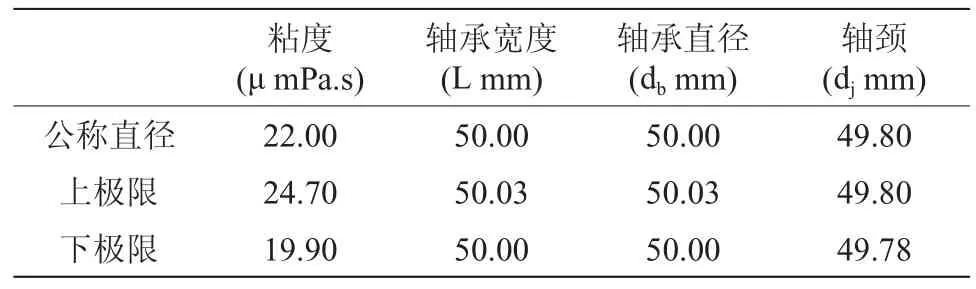
表1 尺寸的上下极限2k因子设计因素水平表
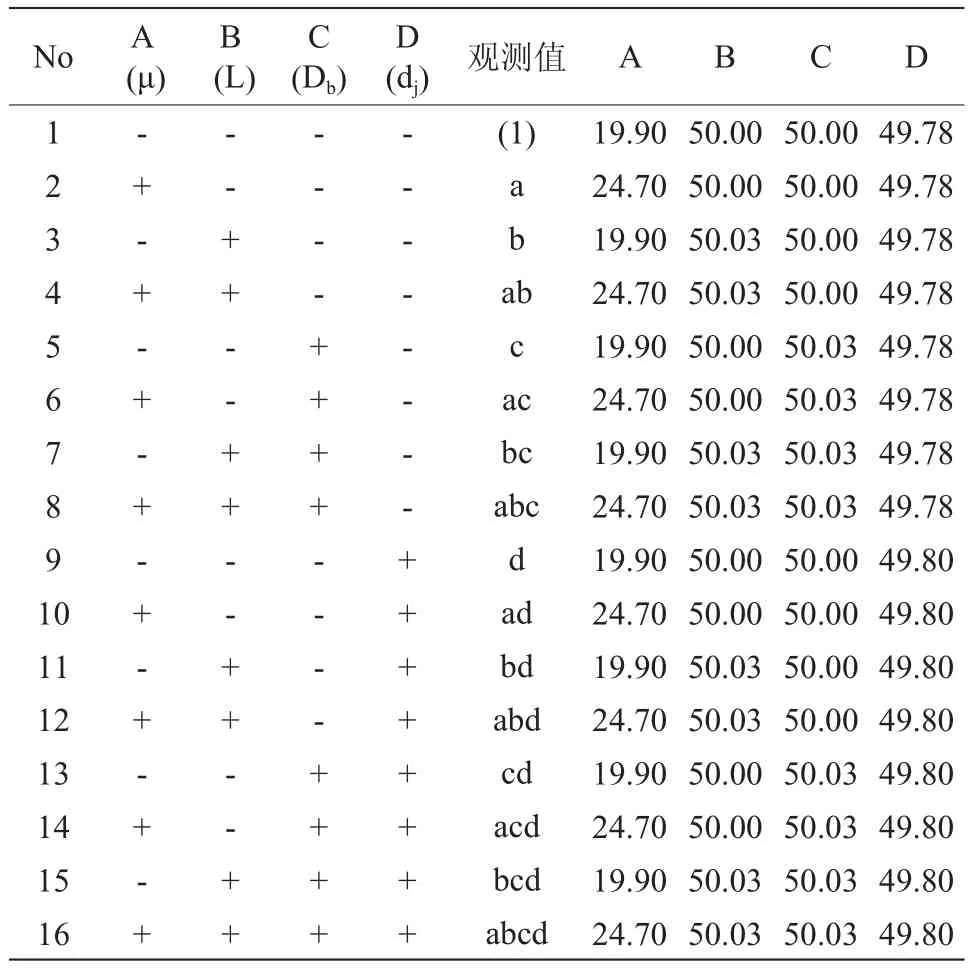
表2 试验数据表
3 试验结果与分析
滑动轴承转子系统的能量损失主要是由电机驱动、油膜涡动以及流体摩擦损失等引起的,而摩擦导致的能量损失占绝大部分[7~9]。摩擦功率是指转子系统在一定转速下克服支承各轴瓦的粘性阻力所消耗的功率,滑动轴承转子系统的粘度、宽度、轴承直径以及轴颈直径等参数对旋转机械能量损失均有影响,在高速运转时尤为明显。在非线性油膜力条件下,本文重点研究各种尺寸的系统产生摩擦的原理,定量地分析计算摩擦损失,改进轴承的结构设计,减少能耗,为滑动轴承转子系统的研究与设计提供了一定的理论参考。
3.1 系统稳定性临界曲线
一般采用无量纲的运行参数Op来表示系统稳定性临界值:
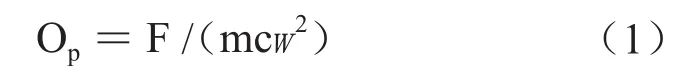
式中,F为滑动轴承载荷,N;m为转子质量,kg;c为径向半径间隙,mm;ω为临界状态转子角速度,r/min。
在Sommerfeld 数与偏心率关系的基础上,当改变系统的某一参数时,如转子质量或流体动力粘度的值,通过计算出轴心轨迹临界点得到系统不同的临界转速,系统的运行轨迹将在坐标系里发生平移,这些临界转速点连在一起,就构成了一条将坐标空间分为稳定区域和不稳定区域的无量纲系统稳定性临界曲线,如图2所示,其结果与Ogrodnik P J等提出的研究结论相符[10]。
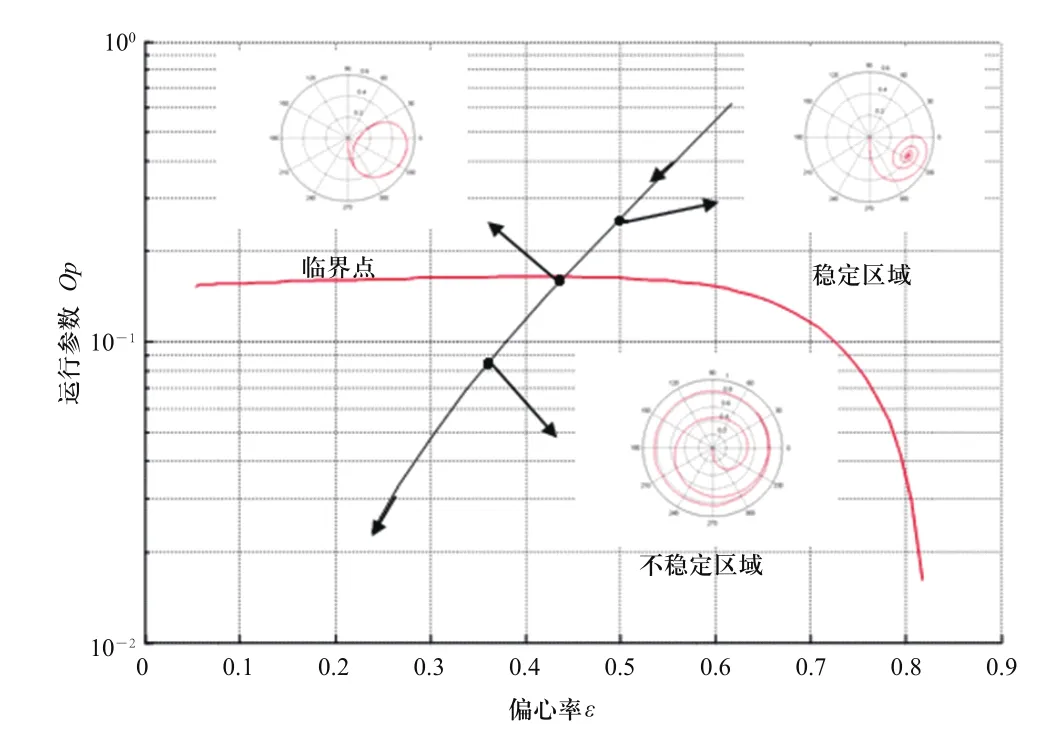
图2 系统稳定性临界曲线
3.2 尺寸误差因子分析与系统功率摩擦损失
影响滑动轴承转子系统摩擦功率损耗的因素很多,涉及系统结构的可靠性和合理性,摩擦功率损失计算公式[11]:
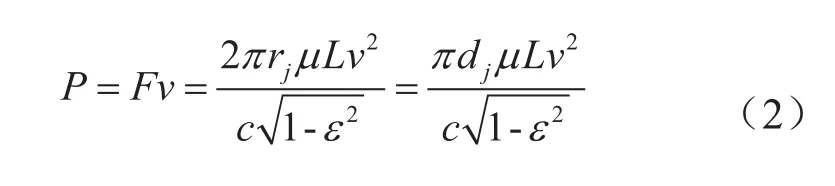
式中,c为轴承的径向间隙,mm;ε为偏心率;dj为轴颈直径,mm;μ为流体的动力学粘度,Pa ·s;L为轴承宽度,mm;v为轴颈的圆周速度,r/min。
由于摩擦功率是通过偏心率在稳定性临界曲线的基础上进行求解,对Op进行2k因子设计分析,便可计算得到摩擦功率的试验结果,对临界运行参数Op的影响如表3所示,各效应的正态概率分布如图3所示。
从正态概率分布的含义可知,在效应因素的正态概率分布图中,与直线拟合不佳离拟合线更远的点通常表示显著效应。而非显著效应值很小通常集中在零附近。从表3以及图3可以看出,在第一种情况下,因子C轴承直径,因子A粘度以及因子D轴颈直径以及它们的交互作用AC对系统稳定临界运行参数Op有非常重要的影响。因子C对Op的影响是消极的,这就意味着因子C的值增加,功率P将会减小,如图4所示为摩擦功率损失曲线,横坐标表示稳定性临界曲线对应的偏心率,纵坐标表示相应的摩擦功率损失。因子A因子D的影响是积极的,这就意味着因子A、D的值增加,功率P也随之增加。由于粘度存在较大的波动因子A粘度的影响最大,如图5、图6所示。
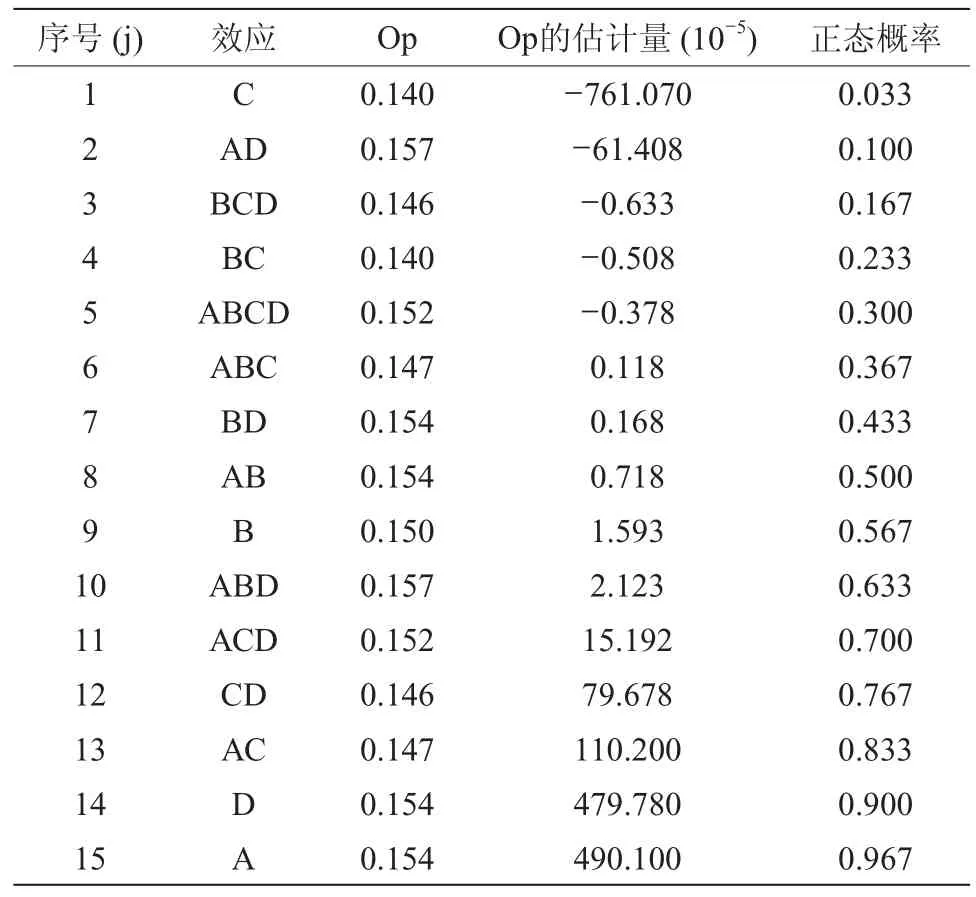
表3 对临界运行参数Op的影响
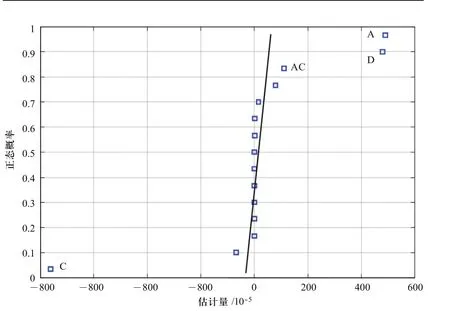
图3 标准概率关系曲线图对Op的影响
根据以上分析,2k因子分析法能高效地判断系统尺寸制造公差对于系统摩擦功率损失的影响大小程度,其中有统计学显著影响的效应因素依次为:轴承直径db(C),动力粘度μ(A),轴颈的直径dj(D)。系统尺寸制造误差通过不同的方式影响系统的稳定界限,增加轴承直径和减小轴颈直径能使系统区域稳定。高水平的变化导致润滑油的动力粘度对系统稳定性影响最大,但是轴瓦直径和轴颈直径对系统摩擦功率的影响也同样重要。
由图4可看出,随着Δdb/c增大临界偏心率变小,系统的摩擦功率上升,故在合理的设计范围内减小轴承直径能有效降低轴承摩擦损耗。图5表明,Δdj/c的增大使得轴承间隙变大,润滑油的流量增大,同时可以减少摩擦接触面积,液力动力润滑的几何条件得到改善,降低了系统的摩擦功率。图6表明,降低润滑油的粘度,能减小动压摩擦阻力,利于减少摩擦损失。
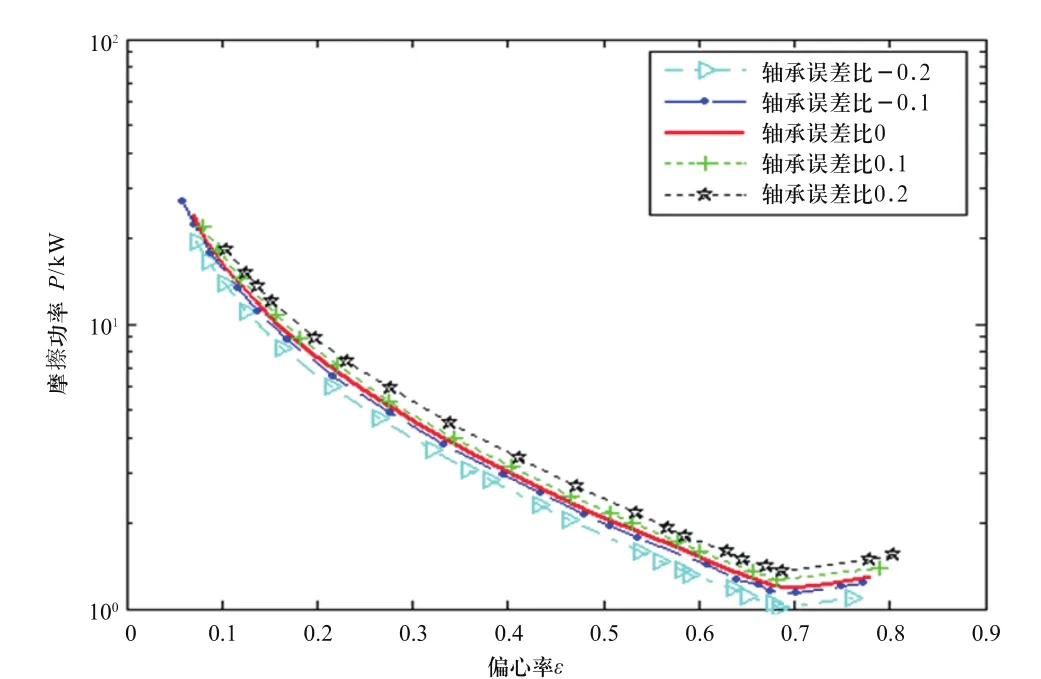
图4 因子C轴承直径误差Δdb/c对摩擦功率的影响
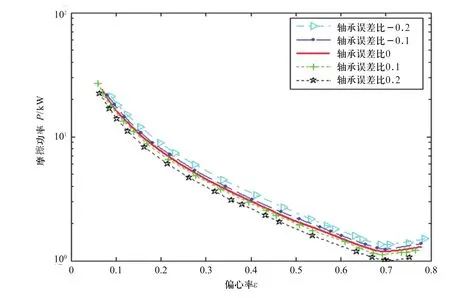
图5 因子D轴颈直径误差Δdj/c对摩擦功率的影响
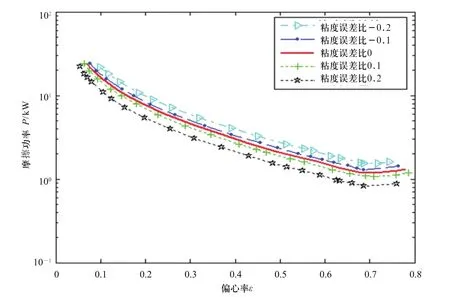
图6 因子A粘度误差μ对摩擦功率的影响
4 结束语
通过建立滑动轴承转子系统的动力学模型,采用2k因子分析方法用来研究各种不同的尺寸误差对系统摩擦功率的影响。研究结果表明,动力粘度、轴承宽度、轴承直径和轴颈直径的尺寸误差对系统稳定性及摩擦功率的影响程度各不相同。
轴承直径误差的增大将导致系统含油量减少,摩擦功率上升,与轴颈直径、动力粘度和轴承宽度误差对系统摩擦功率损失的作用相反,其中动力粘度的影响最大。综合考虑各因子对系统可靠性的作用,找到系统设计的最优方案,经过计算当偏心率在0.6948时系统摩擦功率最小。在设计与制造时合理取值,能够保证系统刚度和精度,有效降低摩擦功率损失,避免盲目设计,提高效率。
[1] 黄文虎, 夏松波, 焦映厚, 等.旋转机械非线性动力学设计基础理论与方法[M].北京: 科学出版社, 2006.
[2] 潘社卫, 金朝铭, 陈卓如, 等.尺寸误差对配合型静压球轴承性能影响的研究[J].哈尔滨工业大学学报, 1998,30(4): 53-56.
[3] 边新孝, 李谋, 渭李威.加工误差对气体静压径向轴承的影响[J].北京科技大学学报, 2005, 27(3): 331-333.
[4] Pierre I, Bouyer J, Fillon M.Thermohydrodynamic behavior of misaligned plain journal bearings: theoretical and experimental approaches [J].Tribology International,2004, 47(4): 594-604.
[5] 徐武彬, 王镇江, 陈其兵, 等.基于Sommerfeld 数的滑动轴承转子系统稳定性分析[J].中国机械工程, 2009,20(23): 2875-2879.
[6] Douglas C.Montgomery.试验设计与分析(英文版·第6版)[M].北京: 人民邮电出版社, 2007.
[7] Kyungbo Bang, Jeonghun Kim, YongjooCho.Comparison of power loss and pad temperature for leading edge groove tilting pad journal bearings and conventional tilting pad journal bearings [J].Tribology International, 2010, (43): 1287-1293.
[8] Padelis G.Nikolakopoulos, Chris A.Papadopoulos..A study of friction in worn misaligned journal bearings under severe hydrodynamic lubrication [J].Tribology International, 2008(41): 461-472.
[9] 张俊岩, 王晓力.高功率密度柴油机主轴承混合润滑特性[J].内燃机学报, 2011,29(1): 90-95.
[10] Ogrodnik P J.Operation of Rotor-bearing Systems Subjected to Dynamic Conical Misalignment [D].Staffordshire, UK: Staffordshire University, 1989.
[11] 巴威尔 F T.轴承系统—理论和实践[M].北京: 机械工业出版社, 1983.

