基于自适应高阶补偿CMOS带隙基准源的设计

王宇星，姜盛瑜 ，吴 金

（1. 无锡科技职业学院，江苏 无锡，214028；2. 海力士半导体中国有限公司，江苏 无锡，214028；3. 东南大学无锡分校，江苏 无锡，214135）

1 引 言

随着集成电路的飞速发展，使得电压基准被广泛用于DC-DC、LDO、A/D、D/A 以及 DRAMS等混合电路中。其要求输出电压不随电源电压、工艺参数和温度的变化而变化。在众多基准电路中，带隙基准（BGR）电路的研究最为广泛[1～5]。高阶补偿方法主要有两类:一种是分段线性补偿[6]，结构相对简单但精度有限；另一种是提取基准中PN结电流非线性量补偿输出电压的非线性量[7]，理论上可达到理想的补偿效果，但补偿控制结构复杂，运放失调等非理想特性的影响使补偿效果难以实现，可控性与稳定性不高。

本文采用基本的分段补偿原理[8～9]，结合自适应负反馈控制结构，实现了一种结构简单且精度高的非线性温度电流补偿结构，将基准温度系数降低到1×10-6/℃以内。

2 高阶补偿原理与结构

2.1 工作原理

一阶线性补偿基准的温度特性为图1（a）所示的开口向上或开口向下的对称分布，为实现高阶补偿降低一个数量级的温度特性，最有效的方法是将一阶线性补偿的单峰极值变为高次补偿下的多峰极值，从而降低基准电压峰-峰值的变化量。为此需适当调节一阶线性补偿量，将原来位于温区中点即常温附近的峰值调整到温区的高温或低温端，与此对应的另一端则通过自适应的高阶补偿形成另一个或多个峰值，通过控制非对称的一阶和高阶补偿关系，使宽温区范围内的纹波电压变化均匀并趋于平衡。

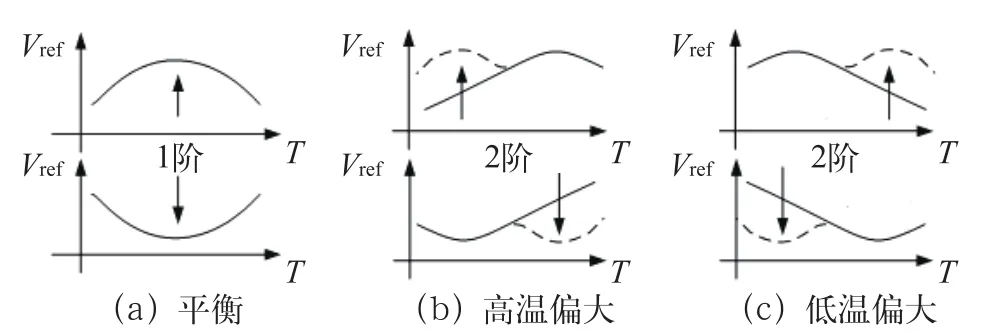
图1 电压基准的补偿温度特性

以开口向下（上）的一阶基准温度特性为例，若一阶基准在高温段输出偏大，如图1（b）所示，则在低（高）温段对输出支路注入适量的负温度系数电流或分流正温度系数电流，以降低低（高）温下的正温度系数，形成低（高）温区下输出基准的局部峰值，并在整个温区内形成双峰输出。同样，若一阶非对称补偿基准的低温值偏大，如图1（c）所示，则需在高（低）温段注入正温度系数电流或分流负温度系数电流，以降低高（低）温下的负温度系数。电流的注入与分流在控制原理上是等效的，针对开口向下的输出特性，合理配置一阶非对称补偿的特性与不同补偿起始点的电流微量控制，即可实现输出“N”型或“M”型的二阶补偿输出特性曲线。

图2给出了基于以上原理实现的一种带隙基准高阶补偿结构，电路的主体部分是基于运放控制的1.2V电压模带隙基准电压，通过调节PTAT限流电阻和输出支路电阻的比例关系，获得图1（a）所示开口向下的一阶基准补偿特性。当采用二阶补偿时，补偿结构如图1（c）所示，应先通过调节电阻比例得到图1（b）中开口向下的一阶带隙基准非对称特性（实线部分），随后通过附加的Mn管的补偿作用，实现二阶补偿特性。

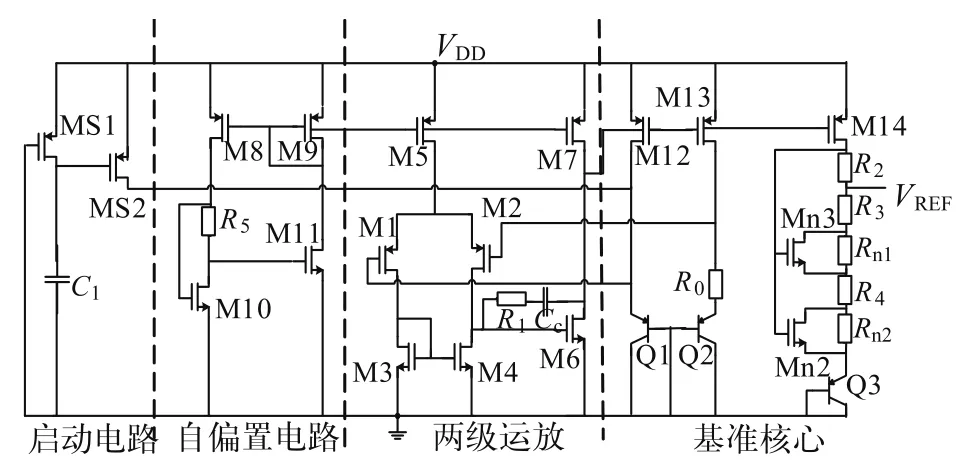
图2 电压模基准补偿电路

2.2 高阶补偿结构

在曲率补偿原理的基础上，利用分段补偿的原理，将全温度范围划分为若干个子区间分段进行补偿[10]，采用如图3所示的自适应高阶补偿输出结构，补偿管分裂成等区间个数的若干个NMOS管。

图3中Mc补偿管的栅电位可在Vref电压附近灵活调节，当VG＞Vref时，补偿管的正温度系数电流调节作用增强；相反，当VG＜Vref时，负温度系数电压调节作用减弱。此外，图3中Mc1与Mc2两个高阶补偿NMOS管的协调配合，可获得两个不同高温起点下负温度系数补偿作用的叠加，实现高阶补偿特性。

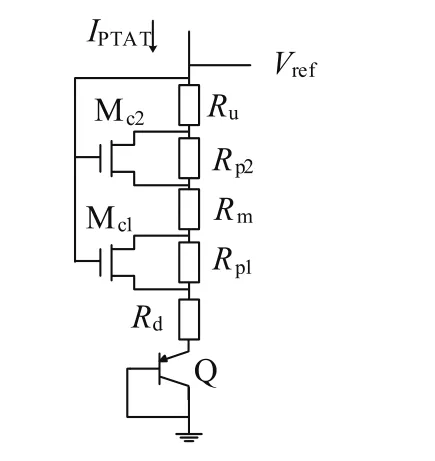
图3 自适应高阶补偿控制结构

3 仿真验证与分析

本电路运用 Cadence Spectre工具，采用CSMC 0.35μm、3.3V CMOS工艺，在-40℃＜T＜125℃范围下进行仿真。

电路补偿是通过并联Mn管来实现的，补偿管温度特性测试如图4，Mn管阈值电压为负温度特性，VGS采用高于基准电压的栅压驱动而具有正温度特性，由此形成Mn正温度系数电流如图5所示。由于Mn 管VGS与VTN之间的有效驱动电压随温度下降而减小，因此当温度下降到某一临界点时，Mn截止。调节Mn管的栅源电压，Mn的补偿作用在整个温区内有效。

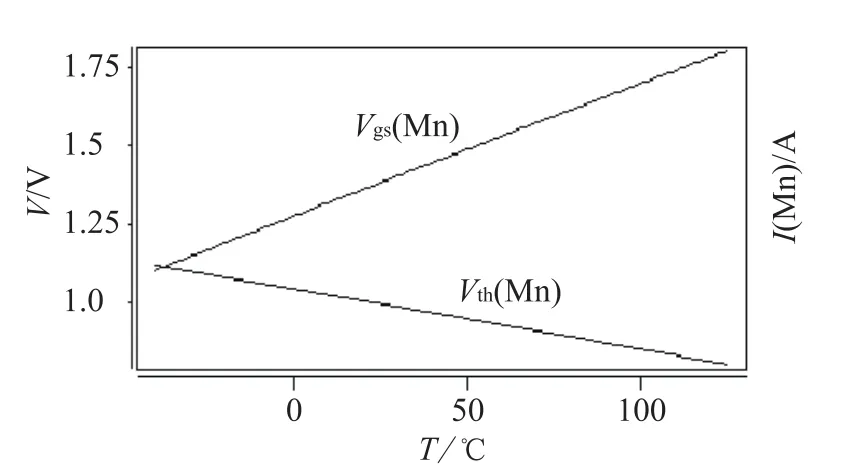
图4 Mn补偿管VGS、VTH温度特性

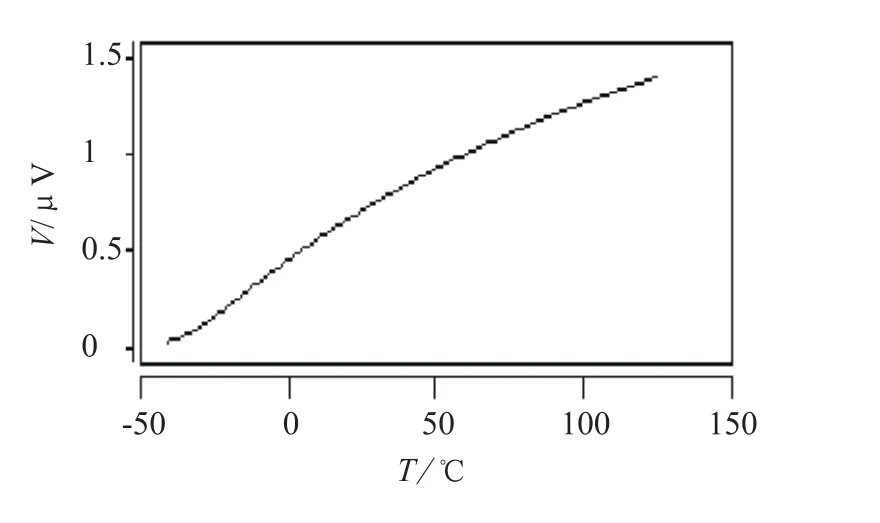
图5 Mn补偿管的电流温度特性

从图4可见Mn管开启很早，全温区补偿，由于Mn管补偿电流随温度增加不断上升，流过并联Rn的电流正温度系数减小，输出电压降低，并且一阶非对称曲线高温段正温度系数的减小程度远大于低温段。

补偿技术后，在-40℃～125℃的温度范围内，基准电压温度系数在五个工艺角下为：0.984×10-6/℃、7.245×10-6/℃、10.17×10-6/℃、4.741×10-6/℃、1.405×10-6/℃。

如图7所示，tt模型下补偿后PSRR在低频100Hz为-60.82dB，10kHz为-29.59dB。电源电压在0～3.3V范围内变化，输出基准电压与电源电压关系如图8所示。当电源电压在2.3V～3.3V范围内变化时，输出基准值为1.3V，其电压值波动为4mV/V。

4 结束语

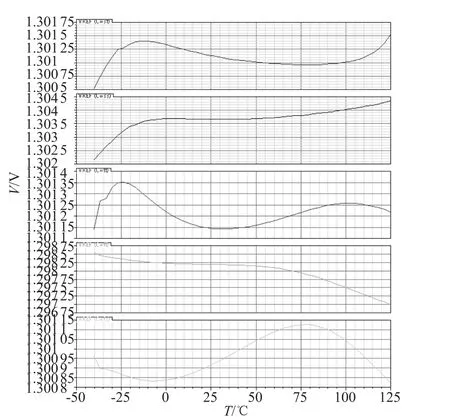
图6 不同工艺角温度特性曲线

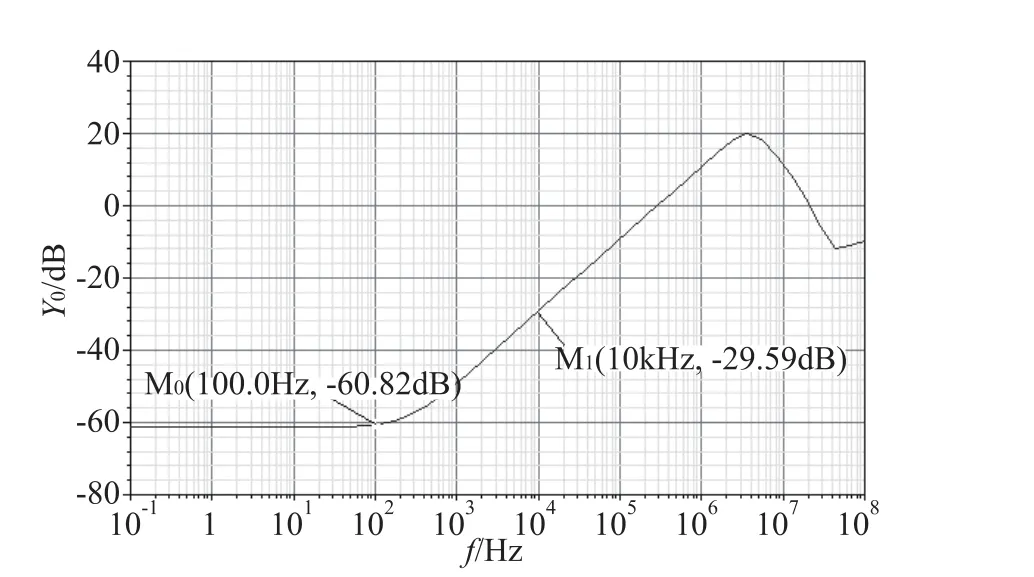
图7 基准电压PSRR特性曲线

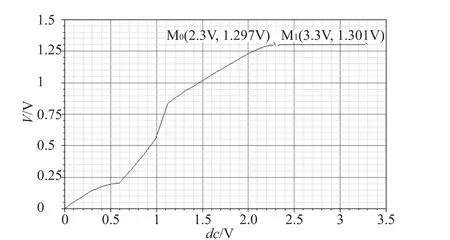
图8 基准电压随电源电压变化特性

本文提出了一种新的电压基准高阶补偿方法。采用分段补偿控制，同时利用输出支路内部自适应负反馈控制，通过在低温段和高温段分别注入或分流不同温度系数的电流，将一阶线性补偿的单峰极值变为多峰极值，将输出电压的变化范围降低到几十微伏的量级。与传统的高阶补偿基准电路相比，新的自适应高阶补偿结构对温度系数的改善十分明显。基于CSMC 0.35μm CMOS工艺的仿真结果表明，3.3V工作电压下，电压模基准在-40℃～125℃温区范围内输出电压变化幅度只有4mV，温度系数仅为0.98×10-6/℃，在高精度低成本方面具有明显的技术优势。

[1] Piero Malcovati ,Franco Maloberti ,Carlo Fiocchi，et al.Curvature-Compensate BiCMOS Bandgap with 1 V Supply Voltage[J] . IEEE Journal of Solid-state Circuit,2001,36 :1076-1081.

[2] Piero Malcovati ,Franco Maloberti ,Carlo Fiocchi，et al.Curvature-Compensate BiCMOS Bandgap with 1 V Supply Voltage[J] . IEEE Journal of Solid-state Circuit,2001,36 :1076-1081.

[3] Andrea B. Op-Amps and startup circuits for CMOS bandgap reference with near I-V Supply[J].IEEE Journal of Solid-Static Circuits,2002,37(10):1339-1343.

[4] Gray P R, Meyer RC., Zhou Ninghua, Chen Yousong ,trans.Analysis and Design of Analog Integrated Circuits[M].Beijing: Higher Education Press,2003.

[5] K N Leung, P K T Mok, C Y Leung. A 2-V 23-μA -5.3×10-6/℃ curvature- Compensated CMOS Bandgap Voltage Reference[J]. IEEE J. SSC, 2003, 38(3) : 561-564.

[6] H. L. Wang, X. Q. Lai, Y. S. Li, et al. A Piecewise-Linear Compensated Bandgap Reference[J]. Chinese Journal Of Semiconductors, 2004, 25(7): 771-777.

[7] P. Malcovati, F. Maloberti, C. Fiocchi,et al.. Curvature-Compensated BiCMOS Bandgap with 1-V Supply Voltage[J]. IEEEJSSC,2001, 36(7): 1076-1081.

[8] Gabriel A. Rincon-Mora, Phillip E. Allen. A 1.1V Current-Mode and Piecewise-LinearCurvature-Corrected andgap Reference[J]. IEEE Journal of Solid-State Circuits,1998,33(10): 1551-1554.

[9] 郑朝霞，邹雪城，等. 一种高精度易扩展的分段线性补偿带隙基准源[J]. 微电子学与计算机，2008，25（8）：33-36.

[10] T. Jiang, H. Z. Yang. Bandgap Reference Design by Means of Multiple Point Curvature Compensation[J].Chinese Journal of Semiconductors, 2007, 28(4):490-495.