PPRTs 偏差方程外推至-189.344 2～156.598 5 ℃温区的研究

王博阳， 曾凡超， 黄安贻， 孙建平， 傅承玉

(1.武汉理工大学,湖北 武汉 430070； 2.湖北省计量测试技术研究院,湖北 武汉 430223； 3.中国计量科学研究院,北京 100029)

1 引 言

航天红外遥感是天基对地观测系统的重要手段，目前对光谱辐射亮度的不确定度要求为0.1 K，对海洋表面温度监测要求为每10年0.04 K的稳定性，对地观测系统红外谱段的稳定性要求优于 0.01 K[1,2]。红外载荷的高精度观测水平需要高精度的定标黑体辐射源维持，而定标黑体辐射源的计量性能由黑体空腔轴向温度均匀性、稳定性、亮度温度的准确度等参数决定[3～5]，这些参数的量值均需要利用铂电阻温度计溯源[6～8]。标准铂电阻温度计(standard platinum resistance thermometer,SPRT)准确度高、稳定性好、性能可靠[9]，但由于体积大且不耐振动，不适用于狭小的测温环境。

精密铂电阻温度计(precision platinum resistance thermometer，PPRT)测量精度介于工业铂电阻温度计和SPRT之间，具有体积小，稳定性好和易安装等特点，常作为精密测温系统中的理想测温元件[10,11]，可安装在定标黑体辐射源内，对其进行多点温度测量[12,13]。

精密铂电阻温度计的标定方法有1990国际温标(ITS-90)定义的固定点法和比较法。固定点法通过使用一组规定的固定点(见表1)和规定的参考函数以及内插温度的偏差函数来分度[14,15]，可以提高PPRTs的测温准确性。但是ITS-90定义固定点数量少且温度间隔大，无法对超出温区范围的温度计进行有效标定[16～18]。

在超出ITS-90定义的温区范围(见表2)，可以对固定点法的偏差方程进行适当外推，对于无法使用固定点法标定的PPRTs，可以使用比较法标定。比较法通过比较测量设定温度点下标准器与待测温度计的电阻值，运用合适的数据处理模型实现温度计的分度。常用的数据处理模型有多项式拟合法与简化的ITS-90公式法。

为了研究ITS-90定义的固定点偏差方程的外推误差大小，李杰等[19]将外推方法运用于PPRTs，将偏差方程上限从29.764 6 ℃外推至70 ℃时，外推误差小于1.6 mK，说明ITS-90定义的固定点法及外推适用于PPRTs，但温度外推范围窄，对-189.344 2～156.598 5 ℃的外推精度未知。王颖文等[20]使用15支SPRTs将第5温区和第11温区偏差方程温区范围外推至-189.344 2 ℃和156.598 5 ℃，外推误差小于20 mK，也证明了SPRTs将ITS-90定义的偏差方程温度范围进行适当外推的可行性。

本文基于ITS-90定义的固定点法和比较法对16支Pt100型PPRTs在温度范围-189.344 2～156.598 5 ℃标定，对超出温度范围的温度计高精度标定进行了研究。

2 基于固定点法的-38.8344～ 0.01 ℃温区偏差方程下限的外推

2.1 数学模型

依据ITS-90定义的内插公式，在 -189.344 2～0.01 ℃温区的偏差方程为：

ΔW4=W(t)-Wr(t)=a4[W(t)-1]+

b4[W(t)-1]·lnW(t)

(1)

式中:ΔW4为-189.344 2～0.01 ℃温区的电阻比偏差;Wr(t)参考函数的电阻比；a4、b4为该温区的温度系数，值由温度计在氩三相点及汞三相点测得的W(t)算出；W(t)为温度计在温度t的电阻值与水三相点温度的电阻值之比：

W(t)=R(t)/R(0.01 ℃)

(2)

但是对于温度下限在-189.344 2～-38.834 4 ℃的PPRTs无法使用式(1)，且ITS-90在汞三相点和水三相点间未定义偏差方程，因此利用汞三相点和水三相点建立等效的新偏差方程如式(3)：

ΔW=W(t)-Wr(t)=a*[W(t)-1]

(3)

式中:a*的值由温度计在汞三相点测得的W(t)算出。结合式(1)、式(3)得到参考函数的电阻比差值ΔWr为：

ΔWr=Wr4-Wr*=(a*-a4)[W(t)-1]-

b4(W(t)-1)·lnW(t)

(4)

式中:Wr4为使用-189.344 2～0.01℃温区偏差方程的参考函数值;Wr*为使用-38.834 4～0.01℃温区新偏差方程的参考函数值。PPRTs的敏感元件为高纯度铂丝，绕线方式与SPRTs相似，可近似认为PPRTs的电阻随温度的变化率与SPRTs一致。将ΔWr代入式(5)可得温度差值Δt：

(5)

式中dWr/dt表示SPRTs电阻随温度的变化率。

同样地，在-189.344 2～-38.834 4 ℃可通过第五温区偏差方程式(6)分度，得到式(7)参考函数的电阻比差值ΔWr，代入式(5)计算出温度差值Δt。

ΔW5=W(t)-Wr(t)=a5[W(t)-1]+

b5[W(t)-1]2

(6)

ΔWr=Wr4-Wr5=(a4-a5)[W(t)-1]+

b4(W(t)-1)·lnW(t)-b5(W(t)-1)2

(7)

通过对比同一温度下新偏差方程和第五温区偏差方程的分度值与标准值温度的差值评判二者的标定精度。

2.2 数据分析

实验对16支PPRTs进行氩三相点、汞三相点、镓熔点和水三相点分度，计算第四温区、第五温区偏差方程和-38.834 4～0.01 ℃温区新偏差方程并将第四温区偏差方程的分度值作为标准值。使用上述方法得到的新偏差方程和第五温区偏差方程在不同分度点与标准值的温度差值见图1，图中黑色实线代表温度差值的平均值，黑色虚线代表温度差值的标准偏差值。在-189.344 2～0.01 ℃范围内以汞三相点 -38.834 4 ℃ 为分界，图1(a)表示新偏差方程的外推误差，图1(b)表示新偏差方程与第四温区偏差方程的非一致性大小，图1(c)表示第五温区偏差方程的外推误差，图1(d)表示第五温区与第四温区偏差方程的非一致性大小。部分分度点的温度差值见表3。

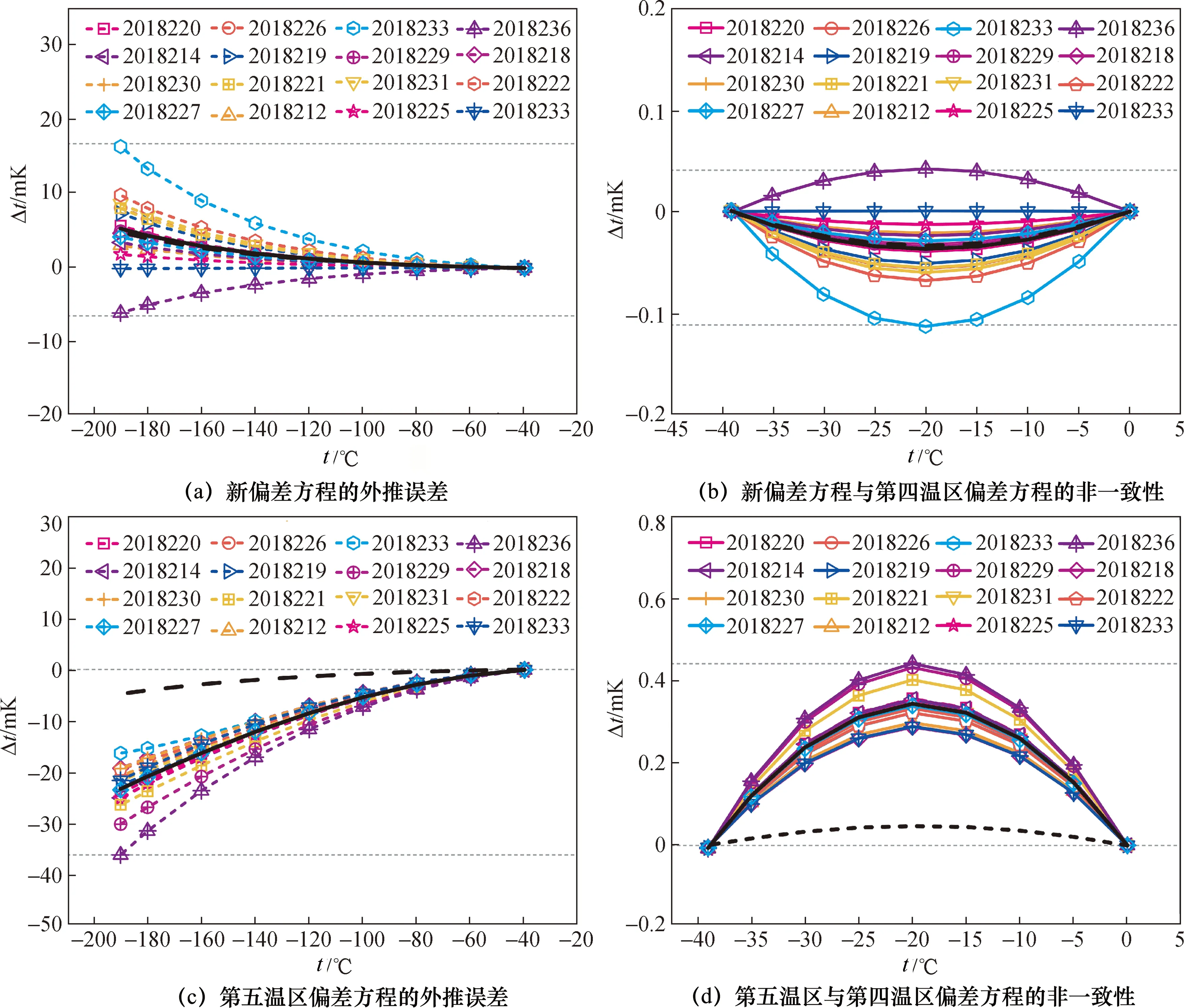
图1 -38.834 4～0 ℃温区新偏差方程和第五温区偏差方程在不同分度点与标准值的温度差值

表3 不同偏差方程的标定精度数据

相同温区下，对比图1(a)和图1(c)，两种偏差方程的外推误差大小存在明显区别:图1(a)中随着分度点的降低，外推误差呈喇叭状扩大；图1(c)中随着分度点的降低，外推误差呈对数增长的趋势。对比图1(b)和图1(d)，2种偏差方程与第四温区的非一致性在-20 ℃时增大到极值,见表3，均小于0.5 mK，证明ITS-90定义的固定点法在低温区适用于PPRTs。

-38.834 4～0.01 ℃温区新偏差方程的外推误差平均值在-189.344 2～-38.834 4 ℃的最大值为5.3 mK，比第五温区偏差方程的外推误差(平均值最大为23.1 mK)减小77%；新偏差方程与第四温区偏差方程的非一致性平均值在-38.834 4～0.01 ℃的最大值为0.04 mK，比第五温区与第四温区偏差方程的非一致性(0.3 mK)提高约一个数量级。新偏差方程的标定结果明显好于第五温区偏差方程，提高标定精度的同时减少对镓熔点装置的使用，提高了分度效率。

3 基于固定点法的0～29.764 6 ℃温区偏差方程上限的外推

3.1 数学模型

依据ITS-90定义的内插公式，在0～156.598 5 ℃温区的偏差方程为：

ΔW10=Wt-Wr(t)=a10[W(t)-1]

(8)

式中:ΔW10为0～156.598 5 ℃温区的电阻比偏差；a10为该温区的温度系数，值由温度计在铟凝固点测得的W(t)算出。对于温度上限介于29.764 6～156.598 5 ℃的PPRTs无法使用式(8)，可以使用第十一温区偏差方程式(9)分度，并由式(10)依次计算出参考函数的电阻比差值ΔWr，代入式(5)可得温度差值Δt。

ΔW11=W(t)-Wr(t)=a11[W(t)-1]

(9)

ΔWr=Wr11Wr10=(a11-a10)[W(t)-1]

(10)

同样，在29.764 6～156.598 5 ℃温区可通过第五温区偏差方程式(6)分度，得到式(11)参考函数的电阻比差值ΔWr，由式(5)计算出温度差值Δt。

ΔWr=Wr5-Wr10=(a10-a5)[W(t)-1]-

b5(W(t)-1)2

(11)

通过对比同一温度下第十一温区和第五温区偏差方程的分度值与标准值温度的差值评判二者的标定精度。

3.2 数据分析

实验对16支PPRTs进行汞三相点、镓熔点、铟凝固点和水三相点分度，计算第五温区、第十温区和第十一温区偏差方程并将第十温区偏差方程的分度值作为标准值。使用上述方法得到的第十一温区和第五温区偏差方程在不同分度点与标准值的温度差值见图2。

图2中黑色实线代表温度差值的平均值，黑色虚线代表温度差值的标准偏差值。在0～156.598 5 ℃范围内以镓熔点(29.764 6 ℃)为分界，图2(a)表示第十一温区与第十温区偏差方程的非一致性大小，图2(b)表示第十一温区偏差方程的外推误差，图2(c)表示第五温区与第十温区偏差方程的非一致性大小，图2(d)表示第五温区偏差方程的外推误差。部分分度点的温度差值见表4。

表4 不同偏差方程的标定精度数据

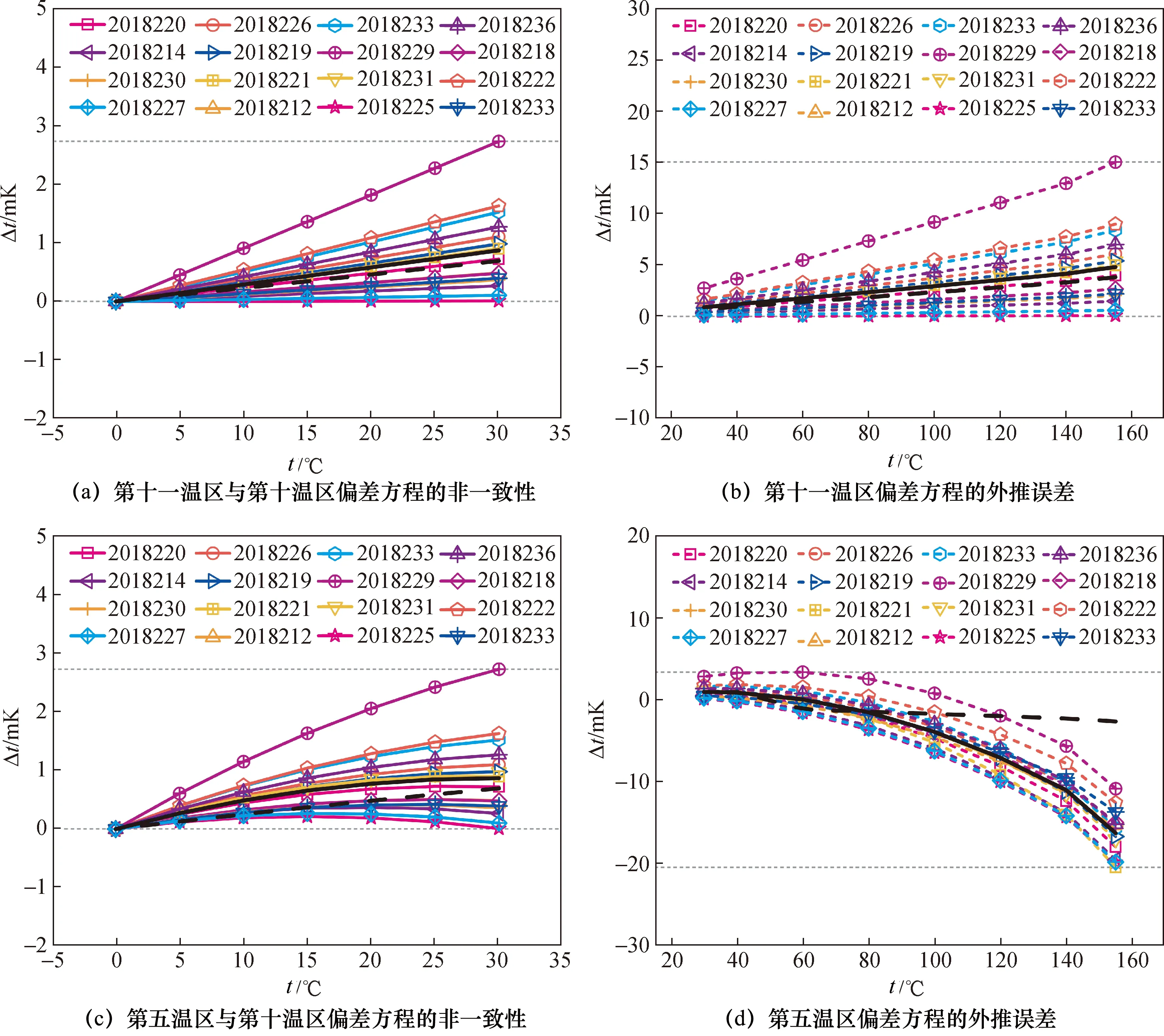
图2 第十一温区和第五温区偏差方程在不同分度点与标准值的温度差值

对于第十一温区偏差方程，如图2(a)、图2(b)，由式(10)可知ΔWr是关于W(t)的一次函数，即得到的Δt应是一条随T增大(减小)而增大(减小)的直线，与图中一致。对于第五温区偏差方程，如图2(c)、图2(d)，由式(11)可知ΔWr是关于W(t)的二次函数，函数的第一个零点为水三相点，第二个零点与温度系数有关。图2(d)中，29.764 6～100 ℃外推误差随分度点的升高变化缓慢，100～156.598 5 ℃外推误差随分度点的升高变化加快，分度点T=156.598 5 ℃外推误差最大,见表4。两种偏差方程与第十温区偏差方程的非一致性小于1 mK，证明ITS-90定义的固定点法在该温区适用于PPRTs。

第五温区和第十一温区的非一致性大小几乎相同。在29.764 6～100 ℃两种偏差方程的外推误差均小于10 mK；在100～156.598 5 ℃第五温区偏差方程外推误差快速增长，总体小于20 mK；第十一温区偏差方程外推误差依旧小于10 mK。第五温区偏差方程由于跨温区(第四温区、第十一温区)外推精度受限，对于温度上限介于29.764 6～156.598 5 ℃的PPRTs推荐第十一温区偏差方程分度，提高标定精度的同时减少对汞三相点装置的使用，提高分度效率。

4 基于比较法的-38.834 4～0.01 ℃和0～29.764 6 ℃温区偏差方程下限和上限的外推

4.1 多项式拟合法标定水平

多项式拟合法通过比较测量在设定温度点下标准器与待测温度计的电阻值后，运用多项式拟合出温度计的R-T曲线，实现对温度计的分度。实验对16支Pt100型PPRTs在-60、-40、-20、0、20、40、60、80、100 ℃温度点进行比较法测量，测量完成后对测量数据进行3次多项式拟合分度，分度值与第四温区和第十温区偏差方程分度标准值的温度差值见图3，图中黑色实线代表温度差值的平均值，黑色虚线代温度差值的标准偏差值。其中，编号为2018236的温度计在经过氮沸点后，封装失效导致水三相点的电阻温度变化约0.3 ℃，不适合本实验的高精度标定。

图3 3次多项式拟合分度与第四温区和第十温区偏差方程分度在不同分度点的温度差值

部分分度点的温度差值见表5。

表5 多项式拟合法与改进数据处理模型的标定精度数据

多项式拟合的缺点是在拟合点范围外造成极大的误差，与图3(a)一致。-189.344 2～-60 ℃的温度差值代表外推误差，随着分度点的降低，外推误差迅速增大，在-189.344 2 ℃ PPRTs的外推误差均超过1.5K,见表5。

图3(b)中-60～100 ℃的温度差值代表内插误差，随着分度点的升高，误差几乎呈水平分布;100～156.598 5 ℃的温度差值代表外推误差，随着分度点的升高，外推误差逐渐增大;分度点T=156.598 5 ℃外推误差最大,见表5。实验结果表明：使用多项式拟合在拟合范围外误差大，不适合PPRTs的高精度标定。

4.2 改进的数据处理模型

基于比较法的实验步骤，在测量设定温度点下标准器与待测温度计的电阻后，参照基于固定点法的-38.834 4～0 ℃温区和0～29.764 6 ℃温区的偏差方程由式(12)、式(13)计算出设定温度点下的温度系数a*(t),a11(t)：

W(t)-Wr(t)=a*(t)·[W(t)-1]

(12)

W(t)-Wr(t)=a11(t)·[W(t)-1]

(13)

(14)

(15)

式中：m,n分别为恒温槽在0 ℃以上和以下的设定温度个数；a*,ti,a*,tj分别代表ti和tj温度下计算的温度系数。

4.3 数据分析

基于比较法的实验过程，通过上式计算出改进数据处理模型后的偏差方程与第四温区和第十温区偏差方程在不同分度点的温度差值,见图4。

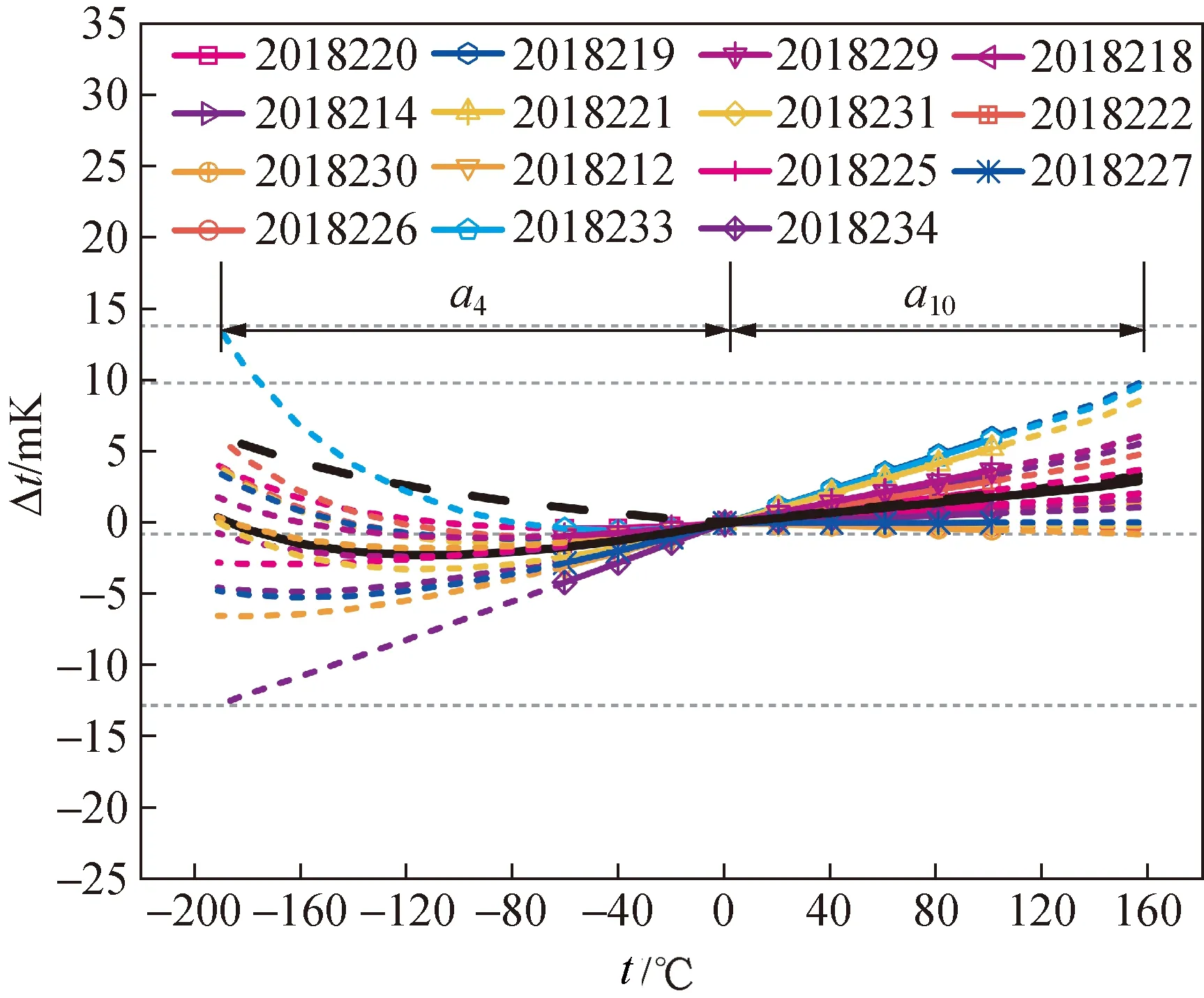
图4 改进的数据处理模型偏差方程与第四温区和第十温区偏差方程在不同分度点的温度差值

对于-189.344 2～0 ℃温区，随着分度点的降低，标定误差逐渐变大；对于0～156.598 5 ℃温区，随着分度点的升高，外推误差逐渐变大。与多项式拟合法相比，改进的数据处理模型在-189.344 2～156.598 5 ℃温区的外推具有更高精度(小于 2.9 mk)，并且在-60～100 ℃温区的内插误差小于1.8 mK，标准偏差小于3.3 mK，优于多项式拟合法(内插误差小于2.8 mK，标准偏差小于9.3 mK)。减少了对固定点装置的使用，同时提高了PPRTs的比较法标定精度。

5 结 论

本文基于ITS-90定义的偏差方程，对-38.834 4～0.01 ℃温区、第五温区和第十一温区偏差方程标定PPRTs的精度水平做出了评价，并针对比较法当前数据处理模型中多项式拟合法标定PPRTs在外推范围误差过大的问题提出了一种改进的数据处理模型，对其在全温区的可行性进行了验证。研究结果表明：

(1) -38.834 4～0.01 ℃温区新偏差方程外推至-189.344 2 ℃的平均最大误差为5.3 mK，优于第五温区偏差方程的外推结果(23.1 mK)；第十一温区偏差方程外推至156.598 5 ℃的平均最大误差为4.8 mK，优于第五温区偏差方程的外推结果(16.3 mK)。采用新偏差方程和第十一温区偏差方程在-189.344 2～156.598 5 ℃温区具备较高的标定精度。

(2) 改进的数据处理模型偏差方程在-189.344 2～156.598 5 ℃温区的平均标定误差小于2.9 mK，在外推范围具有较高的精度。对于该型号PPRTs，三种偏差方程均提高了PPRTs在超出温区范围的外推精度，为星载红外遥感定标的量值溯源及其它工业精密测温系统提供了数据支撑。对于其它型号的PPRTs能否拥有同样的外推精度，尚需进一步的研究及数据积累。