基于ANSYS的铷灯寿命预估与选型数值模拟分析

姚 力， 汪 舟， 王晓丽， 葛久志， 谭理成， 朱 希， 陶海征

(1. 武汉理工大学 汽车工程学院，湖北 武汉 430070； 2. 武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北 武汉 430070； 3. 湖北省计量测试技术研究院，湖北 武汉 430223；4. 武汉理工大学 硅酸盐建筑材料国家重点实验室， 湖北 武汉 430070)

1 引 言

铷原子钟因其体积小、质量轻、功耗低、短期稳定性强等优势，广泛应用于卫星的导航定位[1]。空间应用的需求对铷钟的工作寿命提出了很高的要求。铷光谱灯是铷钟的核心部件之一，研究表明铷灯灯泡中铷原子的损耗是导致铷钟寿命终结的主要原因[2]。因此选用耐碱性玻璃作为铷灯材料，在铷灯内充入足量的铷，是延长铷灯工作寿命的主要思路。但是充铷量过多会导致液态金属铷在铷灯内表面流动，使铷灯输出的光强不稳定，对铷钟整机的频率稳定度产生不利影响[3]。因此，能够准确预测铷光谱灯铷量在不同的服役过程中的消耗速率，根据铷灯中铷消耗特性确定适宜的充铷量，是铷钟寿命设计考虑的核心问题。

对于铷光谱灯寿命的研究，Volk等通过对不同厂家生产的Corning 1720、Schott 8437以及Schott 8436共4款玻璃进行了铷消耗实验研究，验证了铷灯寿命的主要限制因素为铷原子向玻璃外部扩散，并通过实验证明了铷原子扩散到玻璃中的速度取决于铷灯的条件，包括灯的尺寸、玻璃的类型、灯的温度和射频驱动功率等。Cook等人通过进一步实验修正了铷消耗经验公式，针对铷的化学消耗，引入了κ作为化学反应的时间常数，得到了精度更高的铷消耗模型公式[4]。

国内许多的科研机构，如兰州空间技术物理研究所[5～7]和武汉物理与数学研究所[8,9]，近二十年内针对铷灯寿命预测和提高铷灯寿命措施方面进行了一系列研究。何胜国等利用一种新的灯泡赶铷方法，显著提高了差分扫描量热计测量灯泡铷量的精度[10]。通过对长达7年铷量测试数据的理论拟合，得到了误差值小于10 μg的铷量消耗模型公式。

对于目前铷灯内金属铷消耗的研究方法，主要是通过长时间的实验获取相关参数然后通过数据拟合得到经验公式，需要耗费大量的时间和资金成本。随着计算机技术的迅猛发展，数字仿真技术在工业界的各个领域都得到了广泛的应用与发展[11～15]，而有限元方法与其他数值仿真方法如离散元和边界元等相比，无论是在理论完善和商业软件开发方面，近20年来都有着长足的发展，因此在学术界和工业界逐渐成为仿真分析的首选方法。本文基于瞬态热传导方程和非稳态质量扩散方程在数学形式具有相似性这一特点，使用有限元数值模拟方法研究铷原子在铷灯材料中扩散行为规律，同时利用所建立的有限元模型，分析了不同体积铷灯、铷灯外轮廓线曲率对铷消耗量的影响，为进一步预测铷灯的铷量消耗、预估铷灯的工作寿命和铷灯的选型提供有价值参考。

2 铷物理消耗的数学模型

2.1 铷扩散过程原理分析

在铷灯泡服役过程中，当铷吸附在玻璃泡壳内表面后，一般认为铷通过扩散、渗透以及毛细作用等方式侵入玻璃内部，且在大多数情况下均以浓度的扩散为主要方式[16,17]。铷原子在浓度梯度的作用下从浓度高的区域向浓度低的区域进行迁移，在玻璃中只要存在铷浓度差，铷灯内部的铷原子扩散作用就会发生，系统内部铷原子的总量并没有发生改变。铷光谱灯工作时铷量耗散的过程，实质就是铷原子质量转移的过程，因此该过程遵循质量守恒定律和Fick定律[18]。

铷在玻璃中扩散的过程为非稳态扩散，介质内部铷原子的浓度随时间不断发生变化，针对非稳态情况下的扩散特征，Fick第二定律用以描述物质扩散规律的。它指出在非稳态扩散过程中，在距离x处，浓度随时间的变化率等于该处扩散通量随距离变化的负值，即:

(1)

式中:C为扩散物质的质量浓度,kg·m-3;D为扩散系数,m2·s-1;t为扩散时间,s;x为距离,m。且铷在玻璃中的扩散系数仅与温度和玻璃材料有关，则式(1)可更改为:

(2)

2.2 热传导与铷扩散分析对比

热传导实质是由物质中大量的分子热运动互相撞击，而使能量从物体的高温部分传至低温部分，或由高温物体传给低温物体的过程[19]。固体中热的传导，就是能量的迁移，因此热传导过程同时遵循能量守恒原理和Fourier定律。

Fourier定律表明单位时间内通过给定截面的热量，正比例于垂直于该截面方向上的温度变化率和截面面积，且热量传递的方向则与温度升高的方向相反。自然界和工程上的许多导热过程为非稳态，物体的温度随着时间不断变化，需要考虑热平衡方程进行求解。根据能量守恒定律进行推导得到瞬态热传导方程为:

(3)

式中:λ为导热系数,W·m-1·℃-1，是反映物质导热能力的量度;θ为温度,℃;ρ为密度,kg·m-3;c为比热容,J·kg-1·℃-1。

表1是铷原子扩散方程与热传导方程对比分析详细情况，表中罗列了2个控制方程在非稳态情况下的形式、所涉及的物理量以及相关单位的对比情况。从表1的控制方程以及物理量对比情况可得知，热传导方程仅在等式左边比铷原子扩散方程多了密度和比热容2个物理量，故在运用ANSYS中的热传导模块来分析铷的扩散规律时，只需要在数值上令浓度=温度(C=θ)；扩散系数=导热系数(D=λ)；并取密度ρ=1，比热容c=1，即可使扩散方程与热传导方程在控制方程形式上获得统一，从而便可用ANSYS仿真软件中的热传导模块来分析铷原子在玻璃中扩散过程。

表1 扩散方程与热传导方程对比分析

3 铷物理消耗有限元模型

3.1 实验参数

由于仿真模型铷量消耗对比的实验值来自中国科学院频标重点实验室何胜国等人测试结果，因此铷物理消耗有限元模型加载和约束条件与文献[10]铷量消耗测试实验过程一致。在该实验中选取3个铷灯泡进行了长期的剩余铷量测试，所用的铷光谱灯泡为圆柱形，内表面积约为300 mm2，铷灯材料为Schott 8436玻璃。铷光谱灯工作温度为130 ℃，激励电路总功率为1.8 W，射频频率为110 MHz。详细的铷光谱灯铷量测试实验参数如表2所示。

表2 铷光谱灯铷量测试实验参数

3.2 有限元模型建立

圆柱形铷灯泡的剖面图如图1(a)所示。圆柱形气室半径为4 mm，根据文献[10]中实验铷灯内表面积计算得到铷灯高为9.94 mm，整体壁厚为 0.5 mm。考虑铷灯泡结构的轴对称性，为了简化计算，有限元仿真中采用二维旋转轴对称模型，利用Workbench前处理模块建立铷灯泡的二维平面模型，后续将建立好的有限元模型导入Mechanical APDL。单元采用热分析模块2D单元PLANE 55，单元划分时，尺寸为0.1 mm×0.1 mm，整个模型的单元划分图如图1(b)所示，共有725个单元，876个节点。

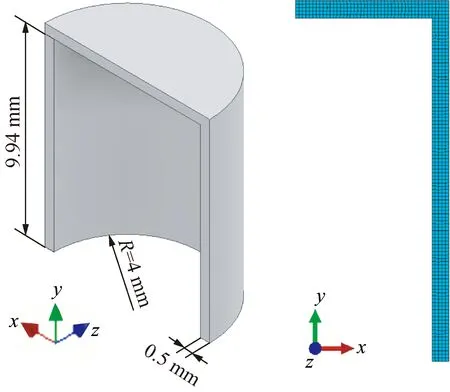
图1 铷灯泡

3.3 材料参数与边界条件

根据表1和表2，热传导模块计算的导热系数用玻璃的扩散系数替代，比热容和密度分别设置为1。初始时刻铷灯模型内表面节点边界条件为初始铷原子浓度，取实验中3个铷灯充铷量的平均值258 μg，铷灯体积为499.64 mm3，计算得到内表面铷原子浓度为0.516 kg·m-3，其余节点设置为0 kg·m-3。具体的载荷和边界条件如图2所示。设置分析类型为瞬态热分析，计算时长设为50年，最后在Post 26后处理模块统计各个时刻模型内表面的铷扩散通量的数据。

图2 铷灯铷量耗散模型边界条件图

4 结果与分析

4.1 仿真结果与实验比较

图3为铷灯内铷原子扩散过程中浓度场云图，观察可发现铷原子在玻璃中的扩散并不全是一维单方向的扩散，对于圆柱形铷灯，上表面与侧面的交线处，铷原子均向x方向与y方向扩散，导致此处的铷的扩散通量值最大。因此在计算铷消耗量时需要分区域讨论铷的扩散状况。观察图4上各处的铷扩散通量值可以发现，无论是上表面还是侧面，在偏离交线处一个壁厚(0.5 mm)的距离后，铷扩散通量值几乎不再衰减。为了精确计算得到铷灯工作过程中的铷量耗散，将铷在玻璃中的扩散区域分为4份，如图5所示。对于A区域和C区域，区域内各节点的铷扩散通量值基本无变化，因此选择图2中的a点与c点作为该区域的代表点计算铷量消耗；对于B区域和D区域，区域内各节点的铷扩散通量值按照远离交线处的方向依次递减，因此选择该区域的中心点，图2中的b点与d点作为该区域的代表点计算铷量消耗。最后累加4个区域的铷消耗量，得到整个铷灯的铷消耗量。

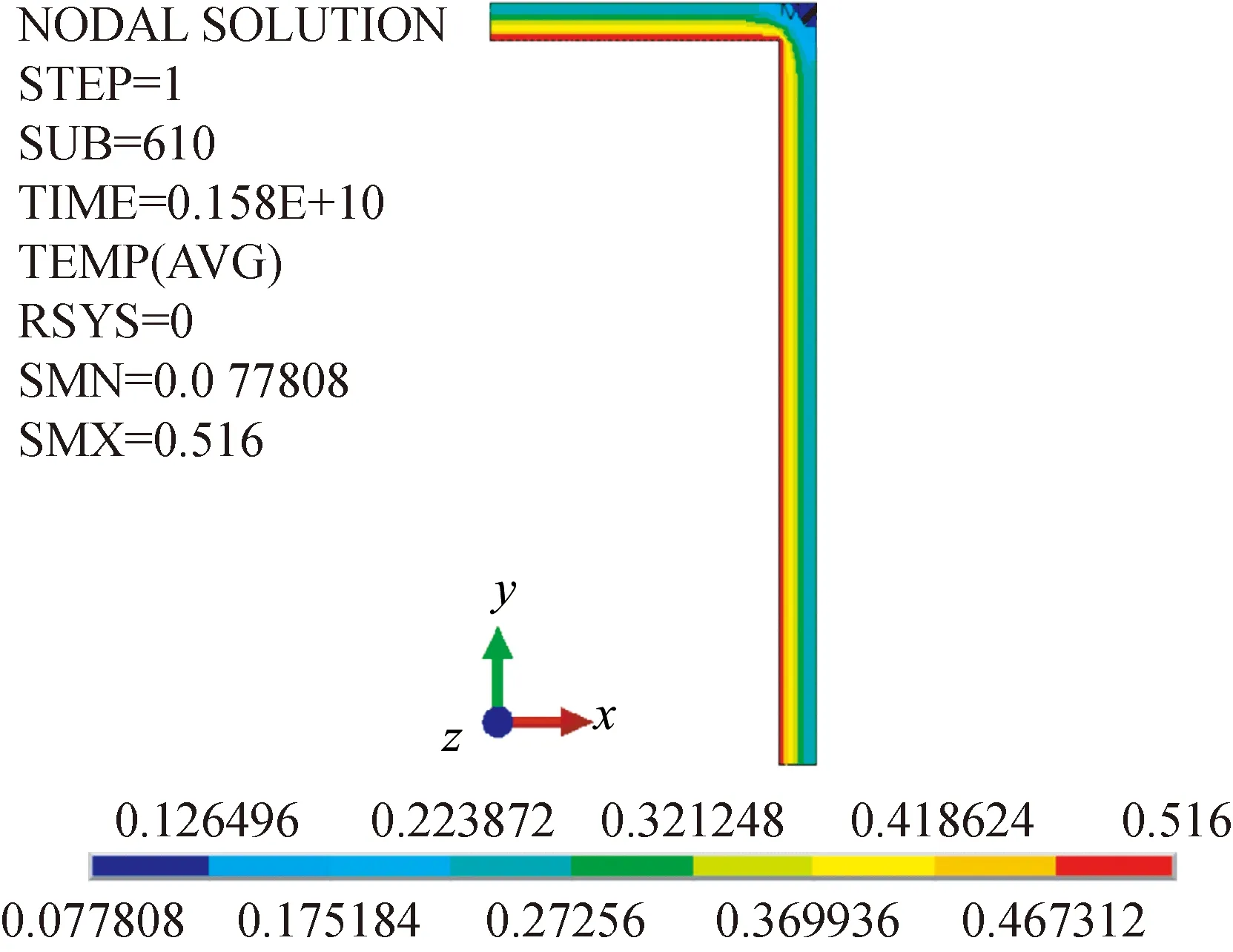
图3 铷扩散过程中浓度场云图

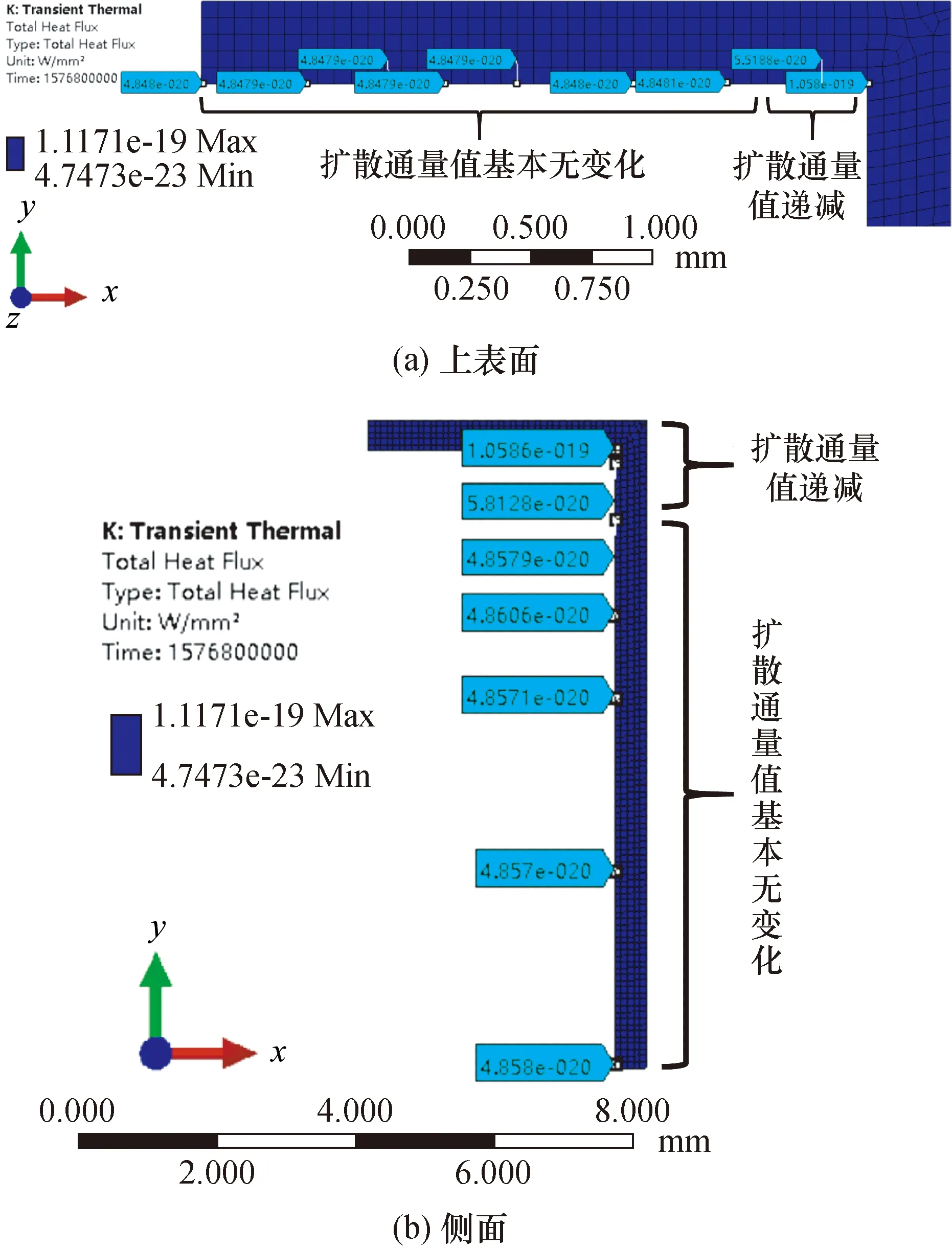
图4 铷灯泡的铷扩散通量

图5 铷灯内扩散区域划分图

图6及图7给出了工作温度(130 ℃)下铷灯泡模型内侧4个区域的铷浓度梯度和铷扩散通量随时间变化趋势图。从图6可以观察到，在铷灯工作初期，由于扩散时间较短，铷灯内表面铷原子较多，侵入玻璃内部的铷原子较少，铷灯内表面4个区域与耐碱玻璃材料之间的铷原子浓度差异都较大，最大可达到5.227 μg·mm-4。较大的浓度梯度造成铷原子大量侵蚀耐碱玻璃材料间隙，导致铷的快速消耗。但随着铷灯使用年限的增长，玻璃内部的铷原子浓度逐渐增大，铷灯内表面与玻璃之间的铷原子浓度梯度逐渐降低。如图6所示，经过2×108s(大约6.34年)后，铷浓度梯度下降了初期时的49.2%。随着铷灯内表面与玻璃之间铷原子浓度梯度的降低，铷灯内部4个区域之间的差异逐渐显现出来，由于交线附近同时受到上表面与侧面的同时侵蚀，相较于侧面与上表面中心处，有着更大的浓度梯度，所以观察后期的铷扩散通量图可以发现B、D区域相较于A、C区域有着更大的铷扩散通量值。具体以B区域各项值为参考，扩散时间为50年，对于铷浓度梯度，D区域为B区域的96.9%，A区域为B区域的85.3%，C区域为B区域的80.8%；对于铷扩散通量，D区域为B区域的96.0%，A区域为B区域的91.4%，C区域为B区域的86.5%。

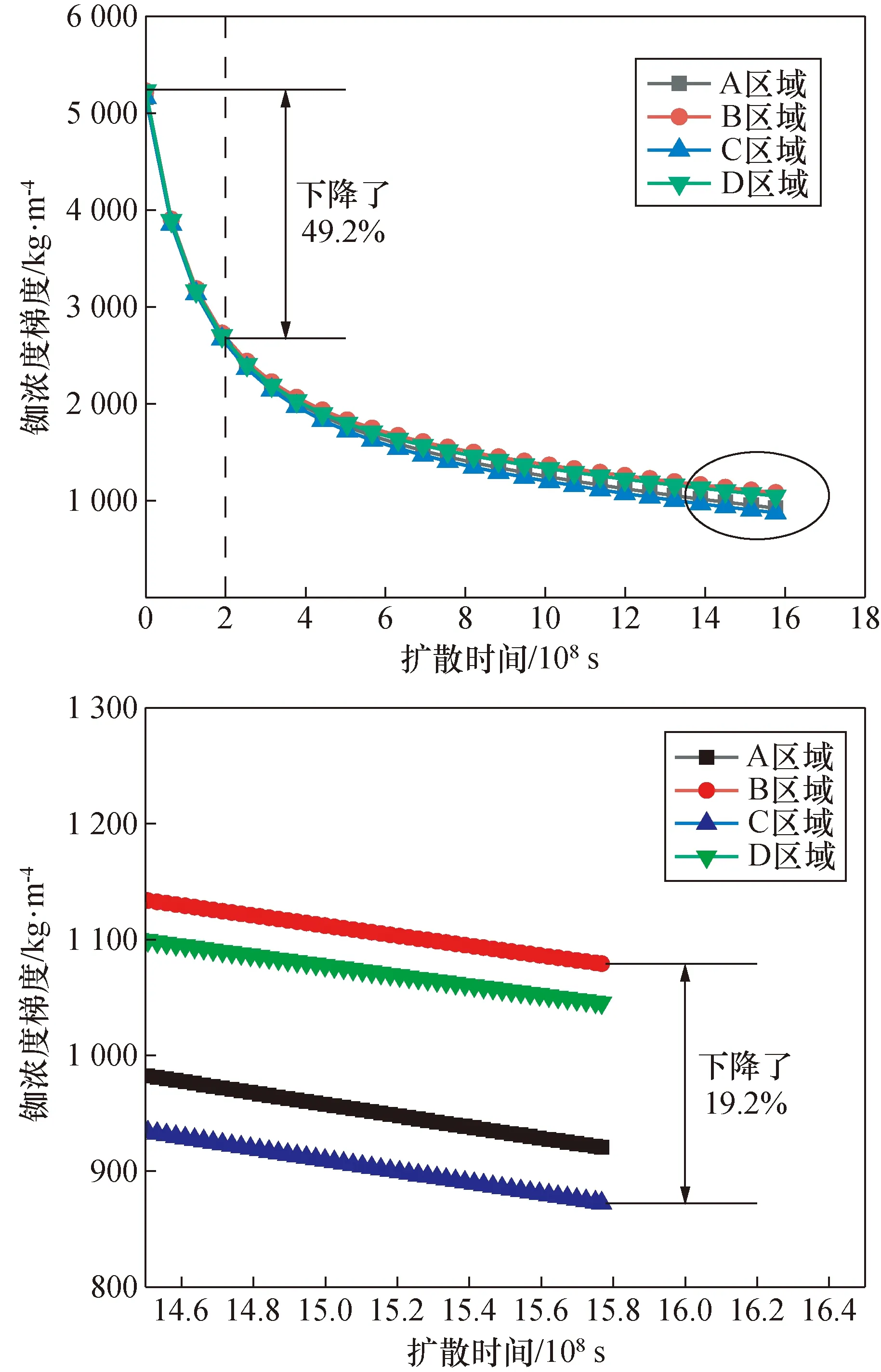
图6 工作温度下铷灯泡内表面4个区域铷浓度梯度随时间变化趋势

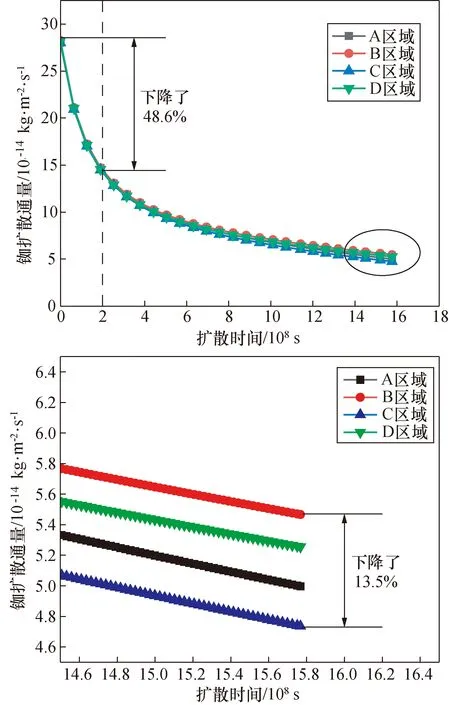
图7 工作温度下铷灯泡内表面4个区域铷扩散通量随时间变化趋势

对铷扩散通量图进行定积分可以得到任意时间段内单位面积上扩散所消耗的铷量，即可以获得铷光谱灯物理消耗的铷量数据，进而能够评估铷灯泡的使用寿命。如表3所示，计算得到了在工作温度(130 ℃)下50年扩散所消耗的铷量。

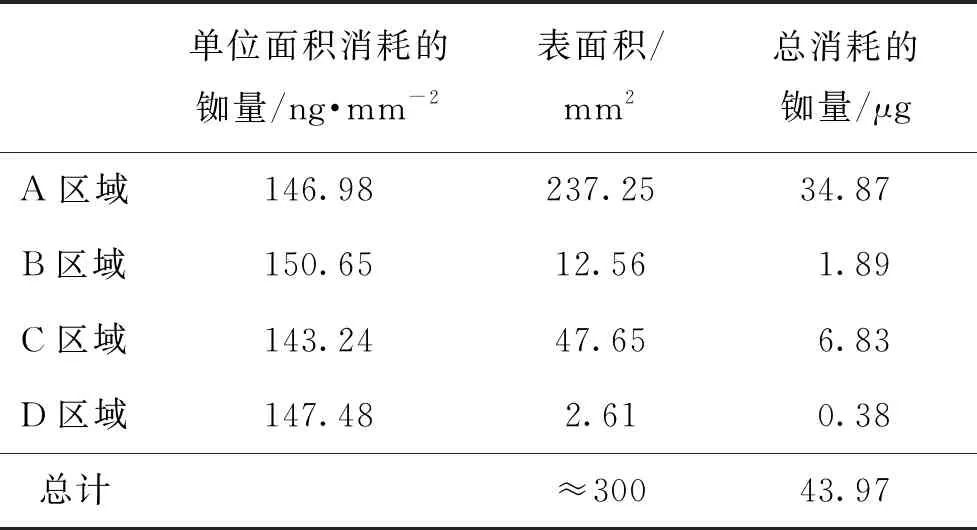
表3 工作温度下50年扩散消耗的铷量

如图8所示，将有限元计算结果与文献[10]中的实验拟合值进行对比发现，有限元计算结果与实验数据拟合结果趋势一致，最大误差出现在75 009 600 s(2.378年)，且最大误差值仅为3.92 μg。根据表4对铷灯工作过程有限元计算结果与实验拟合结果的相对误差分析可以看出，在铷灯工作初期，铷灯内铷量的消耗主要为化学消耗，物理扩散消耗量较少，所以相对误差值较大；待铷灯内杂质与铷原子反应消耗殆尽后，物理扩散消耗为主要消耗，相对误差逐渐减小，有限元计算结果更加精确，即证明使用有限元方法能够正确的模拟铷光谱灯内铷原子的物理扩散消耗，且该方法非常适用于长期工作铷灯的寿命预估。

表4 有限元计算与实验拟合值相对误差分析

图8 实验拟合与有限元数值分析对比图

铷灯在工作过程中，工作温度、耐碱玻璃材料、充铷量以及铷灯的造型都会在不同程度上影响铷原子的消耗。其中工作温度和耐碱玻璃材料的改变会导致铷扩散系数的改变，充铷量的多少会影响铷灯内质量浓度的大小，铷灯造型则会影响铷原子扩散过程中的扩散通量。

4.2 不同体积铷灯对铷消耗量的影响

在获得能够准确预测扩散所消耗的铷量的有限元模型后，为了分析不同体积铷灯对铷消耗量的影响规律，本文在保证铷光谱灯充铷量、内表面积、耐碱玻璃材料及形状相同的情况下，分别选取直径d为6、7、8、9、10 mm，壁厚为0.5 mm的圆柱形铷灯进行铷灯老化实验模拟。为保证圆柱形铷灯内表面扩散面积300 mm2不变，各直径铷灯的高分别为14.42、11.9、9.94、8.36、7.05 mm。计算得到的50年铷消耗量如图9所示。

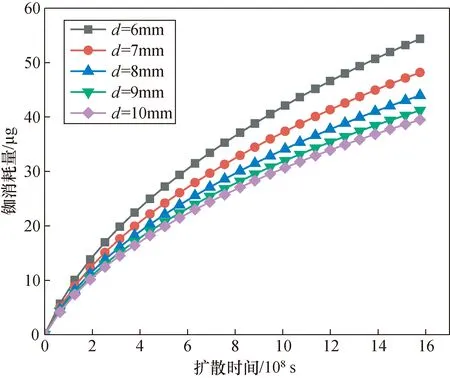
图9 不同直径的铷灯对铷消耗量的影响

观察图9可知，在确保相同扩散面积的前提下，圆柱形的铷灯直径越小，最终消耗的铷量越多。整个仿真过程使用的是同类型耐碱玻璃材料，这消除了扩散系数不同所可能带来的影响。当圆柱形铷灯的直径从6 mm增加至10 mm时，其体积也从407.72 mm3增大至553.71 mm3，最终的铷消耗量也从39.49 μg增长至54.36 μg，增长率为37.7%。其主要原因为5个不同直径的铷灯有着相同的充铷量，这导致体积越小的铷灯内表面的初始铷原子浓度越大，扩散过程中的铷扩散通量至也随之增大，最终导致在相同时间下的铷灯老化实验中有着更多铷消耗量。

4.3 外轮廓线曲率对铷消耗量的影响

由于在满足实际服役过程中的铷灯形状各有不同，不仅有圆柱形，还有梨形，如图10所示。相较于圆柱形铷灯，当梨形铷灯工作时，灯泡内的惰性气体对流时可以使铷灯内的杂质沉积在灯泡的底部，减轻杂质对灯泡壁的污染。本文在保证梨形铷灯充铷量、耐碱玻璃材料及体积相同的情况下，分别选取外轮廓线曲率半r径为5.5、6.5、7.5、10.5、20.5 mm，壁厚为0.5 mm的梨形铷灯进行铷灯老化实验模拟。进一步为了对比相同服役条件下圆柱形铷灯与梨形铷灯的铷量消耗，底座统一为半径4 mm，高 1.5 mm，壁厚为0.5 mm的圆柱，计算得到的50年铷消耗量如图11所示。

图10 梨形铷灯泡

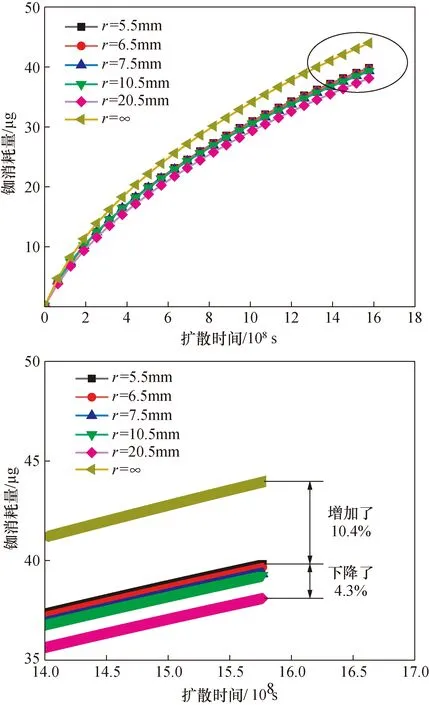
图11 不同曲率半径的铷灯对铷消耗量的影响

曲率半径越大的铷灯，它的外轮廓线越“直”，所以梨形铷灯的不完整球面处发生一维单向扩散的概率就越高，即导致该区域的铷原子浓度梯度相对较低，铷扩散通量值相较于曲率半径小的区域则较小，具体的参数值如图12所示。但观察图11可知，梨形铷灯外轮廓线曲率半径的变化对最终的铷量消耗值影响较小，曲率半径增长率为272.7%时，铷量消耗下降率仅为4.3%。但当曲率半径增至无穷大时，即外轮廓线变为直线，梨形铷灯改变为圆柱形铷灯时，相同的工作温度、耐碱玻璃材料、充铷量及铷灯体积条件下，最终的铷量消耗增长了10.4%。其主要原因为，虽然梨形铷灯的不完整球内表面相较于圆柱形铷灯有着更大的铷扩散通量值，但相同体积和底部直径条件下，圆柱形铷灯的内表面积为300 mm2，梨形铷灯的内表面积仅为271 mm2，这导致了圆柱形铷灯耗散了更多的铷原子。

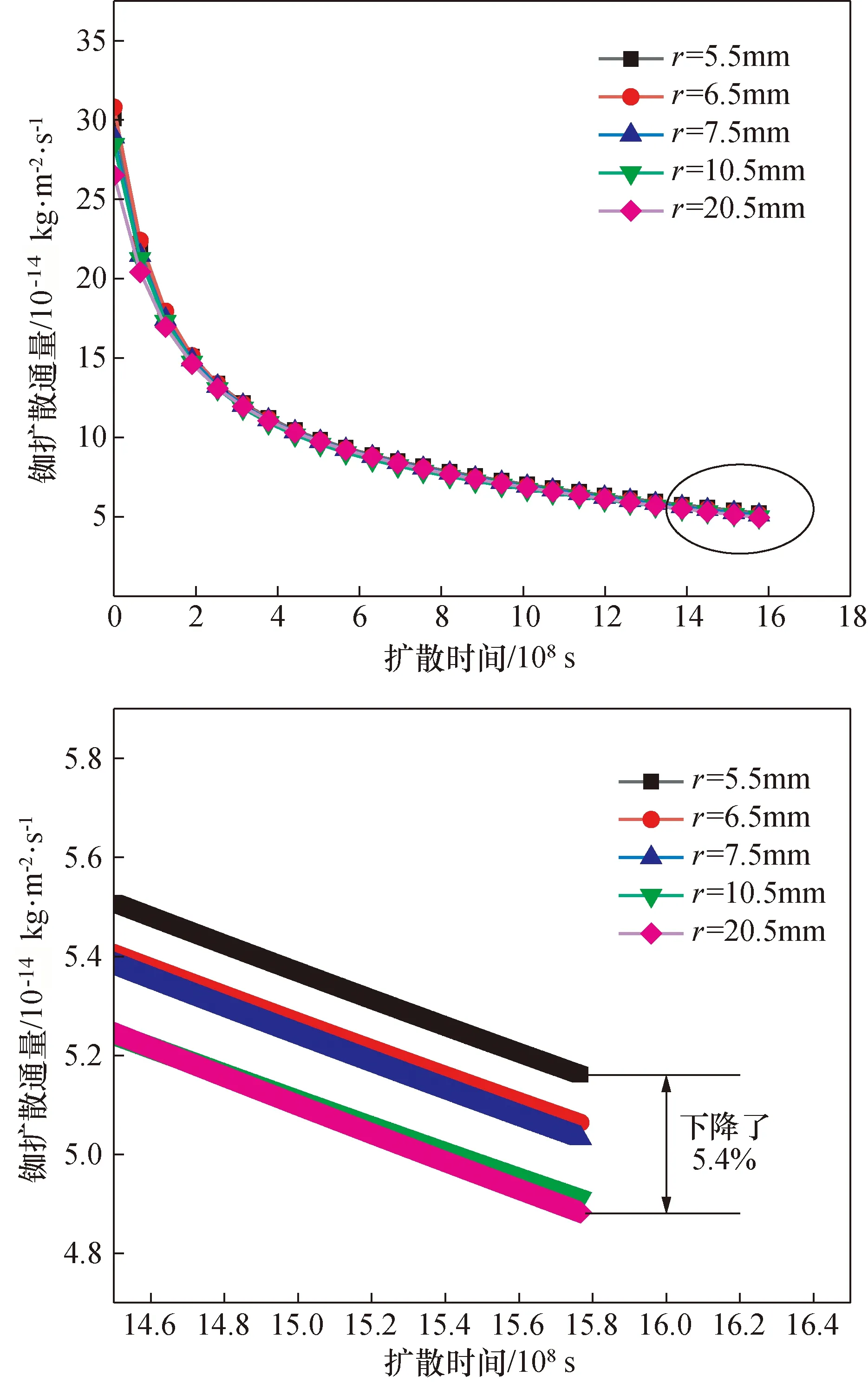
图12 不同曲率半径铷灯的不完整球面铷扩散通量随时间变化趋势

5 结 论

本文以Schott 8436玻璃铷光谱灯为研究对象，通过有限元软件ANSYS建立铷扩散模型，计算得到铷灯工作过程中各时刻的铷消耗量，为预测铷灯的使用寿命提供一种新的方法，并研究了铷灯参数对铷消耗量的影响。结论如下：

(1) 根据瞬态热传导方程与非稳态扩散方程的相似性，利用有限元数值分析方法，对铷光谱灯的铷量消耗能够进行精确的模拟计算。本文计算了50年的铷消耗量，最大误差值为3.92 μg，最大相对误差为14.9%，均出现在铷灯工作初期。且在15年之后，有限元模型计算结果的最大误差值小于2 μg，相对误差小于5%，即证明了使用有限元方法能够准确地计算铷灯的铷消耗量，且该方法更适用于长期工作铷灯的寿命预估。

(2) 对于圆柱形铷灯，保证充铷量与扩散面积相同的情况下，体积最小参数方案的铷灯铷消耗量最大。本文所选取的直径6～10 mm的圆柱形铷灯的铷消耗量最大差值为14.87 μg，最大偏差率可达37.7%。

(3) 对于梨形铷灯，保证充铷量与体积相同的情况下，外轮廓线曲率最大参数方案的铷灯铷消耗量相对较大，当曲率半径增长率为272.7%时，铷消耗量变化率仅为4.3%，即外轮廓线曲率变化对铷灯的铷量消耗影响较小。但当曲率增至无限大即变为圆柱形铷灯时，铷消耗量增加了10.4%，故可认为相同工作条件下，梨形铷灯的铷消耗量更少。