DSP运算方法研究

武乾文，冯 妍

（中国电子科技集团公司第58研究所，江苏 无锡，214035）

1 前言

DSP（Digital Signal Processor）芯片，也称数字信号处理器，是专门为快速实现各种数字信号处理算法而设计的、具有特殊结构、进行高速实时处理的专用微处理器，其处理速度要比最快的CPU还快10～50倍。DSP的典型特征有：每个处理周期能够处理多条乘加操作，具有实时运算能力、实时仿真能力和实时模拟能力，具有很强的通用性、很高的可靠性同时造价低廉。

随着信息技术革命的深入和计算机技术的飞速发展，数字信号处理技术已经逐渐发展成为一门关键的技术学科。业内人士预言，DSP将是未来集成电路中发展最快的电子产品，它将彻底变革人们的工作、学习和生活方式。通过DSP运算方法研究，可以更好地了解DSP结构。

2 DSP的发展及应用

1982年，世界诞生了首枚商用D S P芯片TMS32010，它每秒能处理500万个指令（5 MIPS）。上世纪80年代中期，基于CMOS技术的第二代TMS320C20、TMS320C25 DSP芯片也应运而生，它的存储容量和运算速度都成倍提高，成了图像、语音处理的基础芯片。

上世纪90年代是DSP发展最为迅猛的时期，这主要表现在运算速度进一步加快，集成度进一步提高，功能越来越强大，应用领域越来越广泛。1988年TI公司推出首款浮点DSP——TMS320C3X。1989年TI公司推出业界性能最高的定点DSP产品TMS320C5X。1990年TI公司推出第二代DSP架构的浮点DSP产品TMS320C4X。在1996年TI公司推出TMS320F240。TMS320C6000系列是TI公司于上世纪90年代中后期推出的新一代DSP产品，它们是定点、浮点兼容的DSP序列，TI公司的浮点DSP C6713，频率250MHz，浮点性能1.3GFLOPS。

全球DSP供应商主要是几家美国公司，如德州仪器（TI）、朗讯、模拟器件公司（ADI）、摩托罗拉等等。其中TI处于绝对领先的地位，占据了整个市场份额的45%，其余几家所占份额分别是28%、12%、12%，而其他国家的企业只占到3%。

近10年来，全球DSP产品向着高性能、低功耗、加强融合和拓展多种应用的趋势发展，DSP芯片成为各种电子产品尤其是通信类电子产品的技术核心。据TI预测，到2012年，DSP芯片在单个芯片内将能集成6亿只晶体管。目前，对DSP爆炸性需求的时代已经来临，其主要应用前景十分可观。

3 DSP结构及主要特点

早期的微处理器采用冯·诺依曼（Vo n-Neumann）结构，如图1所示，其片内程序空间和数据空间合在一起，取指令和取操作数都通过一条总线分时进行。当高速运算时，容易出现瓶颈。

DSP芯片的内部采用程序和数据分开的哈佛结构，如图2所示。它允许同时取指令（来自程序存储器）和取操作数（来自数据存储器），而且允许在程序空间和数据空间相互传送数据。具有专门的硬件乘法器，广泛采用流水线操作，提供特殊的DSP指令，可以用来快速实现各种数字信号处理算法。

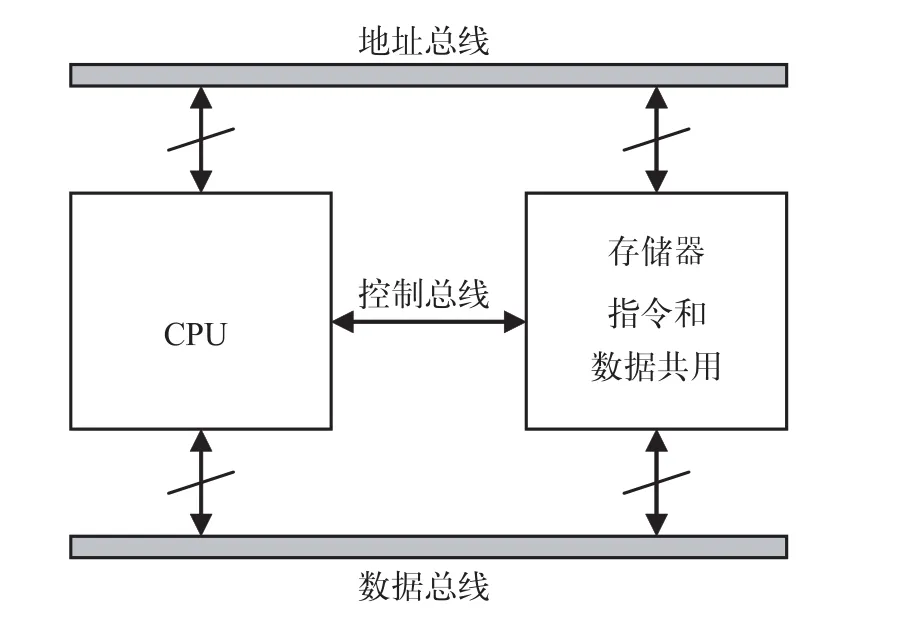
图1 冯·诺依曼（Von-Neumann）结构

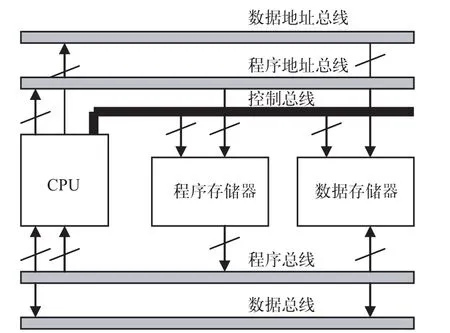
图2 哈佛（Harvard）结构

根据数字信号处理的要求，DSP芯片一般具有如下主要特点：

（1）在一个指令周期内可完成一次乘法和一次加法；

（2）程序和数据空间分开，可以同时访问指令和数据；

（3）片内具有快速RAM，通常可通过独立的数据总线在两块中同时访问；

（4）具有低开销或无开销循环及跳转的硬件支持；

（5）快速的中断处理和硬件I/O支持；

（6）具有在单周期内操作的多个硬件地址产生器。

4 DSP 核心运算功能测试

4.1 DSP数值表示方法

在定点DSP芯片中，采用定点数进行数值运算，其操作数一般采用整型数来表示。一个整型数的最大表示范围取决于DSP芯片所给定的字长，一般为16位或24位。显然，字长越长，所能表示的数的范围越大，精度也越高。以下以16位字长为例。

DSP芯片的数以2的补码形式表示。每个16位数用一个符号位来表示数的正负，0表示数值为正，1则表示数值为负。其余15位表示数值的大小。因此二进制数0010000000000011b＝8195，二进制数1111111111111100b＝-4。

对DSP芯片而言，参与数值运算的数就是16位的整型数。但在许多情况下，数学运算过程中的数不一定都是整数。其中的关键就是由程序员来确定一个数的小数点处于16位中的哪一位。这就是数的定标。

通过设定小数点在16位数中的不同位置，就可以表示不同大小和不同精度的小数了。数的定标有Q表示法和S表示法两种。表1列出了一个16位数的16种Q表示、S表示及它们所能表示的十进制数值范围。

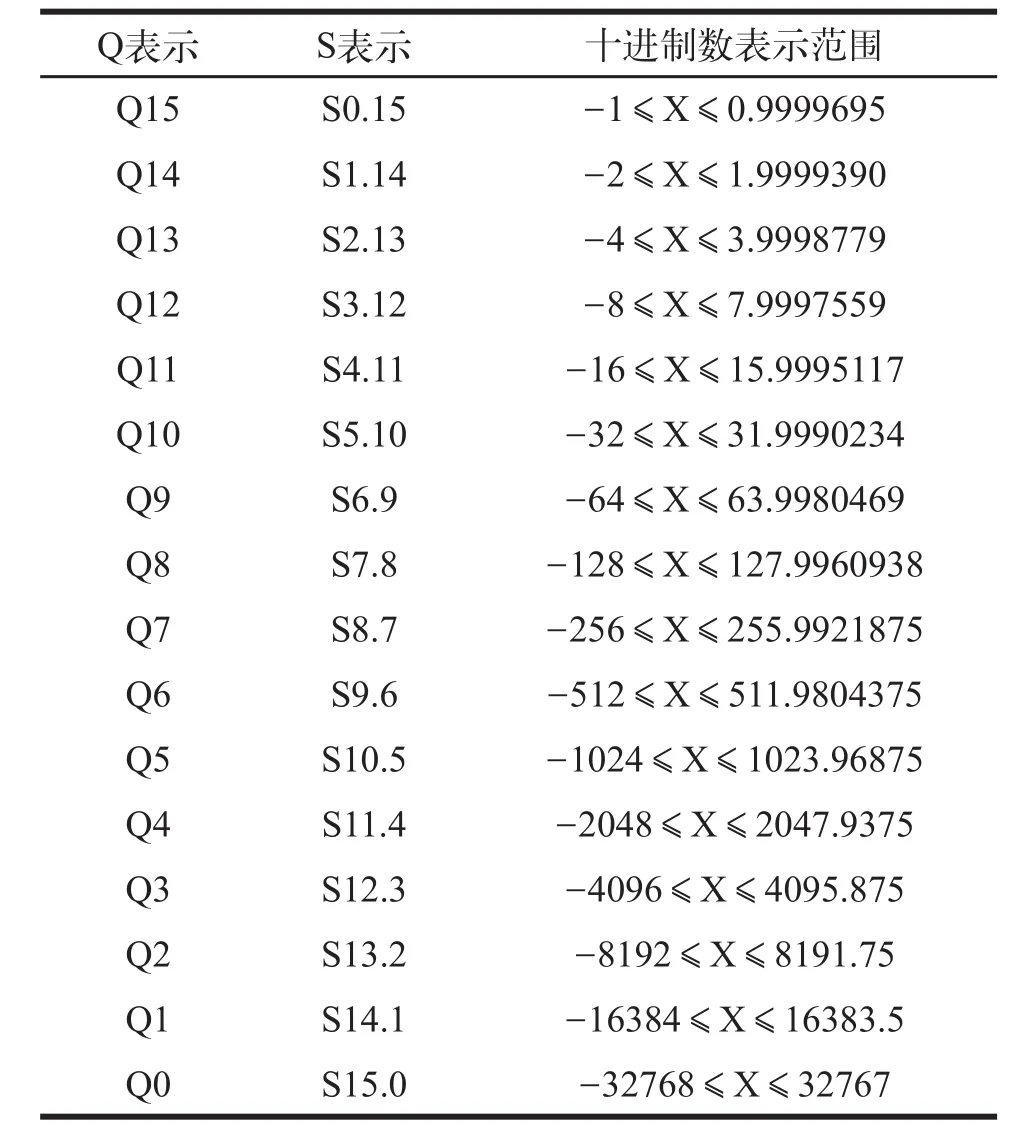
表1 Q表示、S表示及数值范围

从表1可以看出，同样一个16位数，若小数点设定的位置不同，它所表示的数也就不同。例如：16进制数2000H，用Q0表示则等于8192，用Q15表示则等于0.25。

但对于DSP芯片来说，处理方法是完全相同的。

从表1还可以看出，不同的Q所表示的数不仅范围不同，而且精度也不相同。Q越大，数值范围越小，但精度越高；相反，Q越小，数值范围越大，但精度就越低。例如，Q0的数值范围是-32768到+32767，其精度为1，而Q15的数值范围为-1到0.9999695，精度为 1/32768 = 0.00003051。因此，对定点数而言，数值范围与精度是一对矛盾，一个变量要想能够表示比较大的数值范围，必须以牺牲精度为代价；而想提高精度，则数的表示范围就相应地减小。

4.2 DSP乘法

硬件乘法器是DSP的重要组成部分。乘法速度越快，DSP处理器的性能就越高。在通用的微处理器中，乘法指令是由一系列加法来实现的，故需许多个指令周期来完成。相比而言，DSP芯片的特征就是有一个专用的硬件乘法器。在TMS320系列中，由于具有专用的硬件乘法器，乘法可在一个指令周期内完成。主要指令有：

其中三条指令用来将乘数装入到乘法器电路（LT）、移动数据（DMOV）以及将乘法结果（存在乘积寄存器P中）加到ACC中（APAC）。在典型的通用微处理器中，每个乘法需要30 ～ 40个指令周期，而TMS32010只需4条指令。如果采用特殊的DSP指令或采用 TMS320C6201等新一代的DSP芯片，可进一步降低乘法的计算时间。

两个定点数相乘时可以分为下列三种情况：（1）小数乘小数

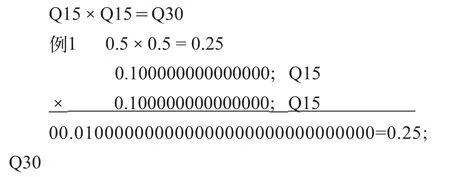
两个Q15的小数相乘后得到一个Q30的小数，即有两个符号位。一般情况下相乘后得到的满精度数不必全部保留，只需保留16位单精度数。由于相乘后得到的高16位不满15位的小数精度，为了达到15位精度，可将乘积左移1位，下面是上述乘法的程序：

（2）整数乘整数

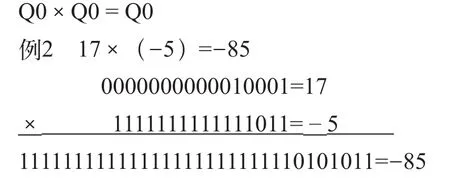
（3）混合表示法

许多情况下，运算过程中为了既满足数值的动态范围又保证一定的精度，就必须采用Q0与Q15之间的表示法。比如，数值1.2345，显然Q15无法表示，而若用Q0表示，则最接近的数是1，精度无法保证。因此，数1.2345最佳的表示法是Q14。

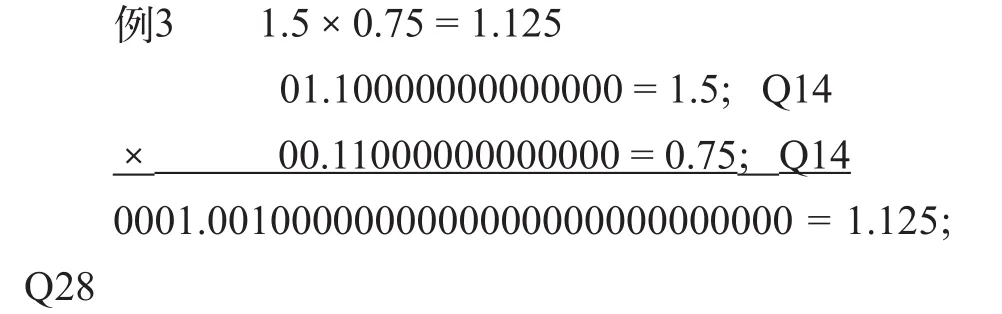
Q14的最大值不大于2，因此，两个Q14数相乘得到的乘积不大于4。当了解到上述乘积不会大于1.8，就可以用Q14数表示乘积，而不是理论上的最佳情况Q13。程序如下：

上述方法为了保证精度均对乘的结果舍位，结果所产生的误差相当于减去1个LSB（最低位）。采用简单的舍入方法，可使误差减少二分之一。

4.3 DSP加法

乘的过程中，测试程序可不考虑溢出而只需调整运算中的小数点。而加法则是一个更加复杂的过程。首先，加法运算必须用相同的Q点表示；其次，程序员或者允许其结果有足够的高位以适应位的增长，或者必须准备解决溢出问题。如果操作数仅为16位长，其结果可用双精度数表示。下面说明16位数相加的两种途径。

（1）保留32位结果

（2）调整小数点保留16位结果

加法运算最可能出现的问题是运算结果溢出。部分DSP提供了检查溢出的专用指令BV，此外，使用溢出保护功能可使累加结果溢出时累加器饱和为最大的整数或负数。当然即使如此，运算精度还是大大降低。因此，最好的方法是完全理解基本的物理过程并注意选择数的表达方式。

4.4 DSP除法

在通用DSP芯片中，一般不提供单周期的除法指令，为此必须采用除法子程序来实现。二进制除法是乘法的逆运算。乘法包括一系列的移位和加法，而除法可分解为一系列的减法和移位。下面来说明除法的实现过程。

设累加器为8位，且除法运算为10除以3。除的过程就是除数逐步移位并与被除数比较的过程，在每一步进行减法运算，如果能减则将位插入商中。

由于DSP没有专门的除法指令，使用条件减指令SUBC可以完成有效灵活的除法功能。使用这一指令的唯一限制是两个操作数必须为正。程序员必须事先了解其可能的运算数的特性，如其商是否可以用小数表示及商的精度是否可被计算出来。这里每一种考虑可影响如何使用SUBC指令的问题。

与DIV_A相同，这个程序中，分子在NUMERA中，分母在DENOM中，商存在QUOT中，TEMSGN为暂存单元。FRAC中规定商的精度，如商的精度为Q13，则调用程序前FRAC单元中的值应为13。

5 结论

本文简要介绍DSP的计算原理和方法，根据其运算原理，可以直接编写汇编指令生成测试向量。DSP直流参数与交流参数的测试相对简单，与普通逻辑电路相同，这里就不再详细介绍。

[1] 苏涛，等. DSP实用技术[M].西安：西安电子科技大学出版社，2002.

[2] 刘益成. TMS320C54x DSP应用程序设计与开发[M].北京：北京航空航天大学出版社，2002.

[3] TMS320C54x Instruction Set Simulator Technical Overview(Rev.A)(spru598a.pdf)[P].Texas Instruments.

[4] TMS320C54x DSP Programmer’s Guide(spru538.pdf) [P].Texas Instruments, 2001.

[5] TMS320C54x DSP Applications Guide Reference Set Volume 4(spru173.htm) [P].Texas Instruments, 1996.