自动扶梯载客输送能力的实证分析*

翁小雄 李俊

(华南理工大学土木与交通学院∥亚热带建筑科学国家重点实验室，广东广州510640)

自动扶梯是带有循环运行梯级的连续载人升降装置，具有载客能力大等特点，广泛应用于商场、车站、机场、地铁等客流量较大场所.自动扶梯载客能力可以参考交通工程学中通行能力的定义［1］，通行能力为不同运行质量情况下单位时间内所能通行的最大交通量，即指定的交通运行质量条件下所能承担交通的能力.按作用性质可分为基本通行能力、可能通行能力、设计通行能力3种.

文中，参考道路通行能力的定义，将自动扶梯的载客能力分为理论载客能力(即设计通行能力)与实际载客能力(可能通行能力).参考《自动扶梯和自动人行道的制造与安装安全规范》［2］，自动扶梯理论载客能力为

式中:c为理论载客能力，人/h;v为额定速度，m/s;k为系数.对常用的宽度Z，当Z=0.6 m时，k=1.0;Z=0.8m 时，k=1.5;Z=1.0m 时，k=2.0.

交通学中理论通行能力是按最小车头时距计算的:

式中:c单位为人/s.

由式(1)、(2)，且将c的单位换为人/s，则有

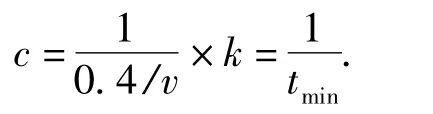
因此，将自动扶梯的理论载客能力对应为道路设计通行能力是可行的，而道路通行能力的确定必须与运行质量相联系，同时需考虑道路、交通、控制及环境条件，因此在分析自动扶梯的载客能力时也要考虑扶梯所处的交通环境、交通量、扶梯外特性等因素.

国内外学者对自动扶梯的实际载客能力做了一些研究.在外国，Paul等［3］主要考虑扶梯运行速度、垂直高度与梯级宽度等因素拟合得到自动扶梯实际载客能力的多元回归方程，但是这一方程假设扶梯左边行走，右边站立，不符合中国的国情;Fruin［4］考虑行人的心理空间，提出“空梯现象”的概念，即不是每个梯级都被占用，这就降低了扶梯的实际载客能力;波特兰州立大学学者认为行人到达的离散性，行人登上扶梯时的迟疑性等将减小自动扶梯的实际载客能力［5］;另外一些学者对行人的交通特性进行了相关研究［6-8］.

国内，田晨［9-10］从梯级宽度、运行速度等多个方面分析了自动扶梯的实际载客能力;陈峰、李三兵等［11-12］通过对现场实测数据分析得到自动扶梯的实际载客能力远小于理论载客能力的结论，但其数据统计量过少，统计方法过于简单;柳伍生等［13-14］对地铁楼梯交通特性的分析方法对自动扶梯的研究有一定的借鉴意义.

这些研究主要从人体生理尺寸、心理因素、自动扶梯提升高度、运行速度等方面考虑自动扶梯的实际载客能力，没有从交通的角度出发，考虑交通环境、交通特性对扶梯实际载客能力的影响，特别是扶梯入口段与扶梯段的行人特性的影响.为了研究交通特性对扶梯实际载客能力的影响，文中选定特定的交通环境即广州地铁，通过拍摄录像与人工计数相结合的方法，实测该交通环境下扶梯入口段与扶梯段的交通特性数据，对这些数据进行处理，建立一定梯级宽度下自动扶梯入口段与扶梯段的行人交通基本图，并从基本图出发，分析扶梯入口段与扶梯段的交通特性，得到自动扶梯的实际载客能力.

1 自动扶梯外特性

1.1 自动扶梯结构

自动扶梯是带有循环运行梯级，用于向上或向下倾斜输送乘客的固定电力驱动设备［2］.自动扶梯按行人的交通特性可分为3个部分，即扶梯入口段、扶梯段、扶梯出口段.如图1所示.

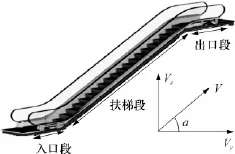
图1 自动扶梯结构图Fig.1 Diagram of escalator structure

1.2 行人交通特性

行人在扶梯入口段、扶梯段、出口段的交通特性各不相同.在入口段，行人的交通特性类似于通道处的交通特性，即在高密度情况下表现出走走停停的蠕动状态，行人的速度、流量受密度的影响较大.当行人踏上水平梯级，即进入扶梯段后，行人的速度即为扶梯的运行速度(不考虑行人在扶梯上行走)，行人密度仅受扶梯梯级宽度与扶梯运行速度的限制.在扶梯出口段，行人运动空间大，行人处于自由流状态，交通特性较简单，因此，本次研究主要考虑扶梯入口段与扶梯段的行人交通特性，不考虑扶梯出口段.

2 实证分析

为了研究交通特性对扶梯实际载客能力的影响，选取广州地铁这个大的交通环境，通过实际数据调查，整理得到基本状态参数，画出自动扶梯的交通基本图.考虑到广州地铁体育西路站为枢纽中心站，乘客下车后将在短时间内通过自动扶梯换乘或者出站，形成脉冲式的拥挤状态，交通特性丰富，因此选取该站点作为试验点，并选择2010-03-15、2010-03-19、2010-03-23、2010-04-06 的下午 4:30—6:30 晚高峰时段，采用拍摄录像与人工计数相结合的方法，获取自动扶梯入口及扶梯上的交通数据.

2.1 状态参数

流量、密度、速度是表征交通流特性的3个基本参数，在进行交通流特性研究时，需要对这3个参数进行各自独立的统计.本次视频数据的处理，采用10s的统计间隔，具体统计与计算方法如下.

流量表示单位时间内通过单位宽度的人数，单位为人/(m·s).统计10 s内通过固定观测断面的行人数，将此人数除以10得到流率，然后用流率除以断面有效宽度得到流量值.

密度表示单位面积内可容纳的人数，通常用来描述拥挤程度，单位为人/m2.统计10 s内任一瞬间扶梯入口段的人数，考虑到10 s内密度仍有一定的变化，文中统计了10 s内任意3个瞬间扶梯入口段内的行人数，取这3个瞬间值的平均值作为该10 s任一瞬间扶梯入口段的人数，用人数除以扶梯入口段面积即得该区域的密度值.

速度表示单位时间内通过的距离，单位为m/s.同密度处理方法一样，统计10 s内任意3个行人进入与离开扶梯入口段的时间，用这3个时间差的平均值作为行人通过扶梯入口段的时间，然后用扶梯入口段的长度除以该时间即得速度.

2.2 实证方法

2.2.1 录像法

扶梯入口段，由于人流从一个相对宽敞的环境进入到狭窄的环境，交通特性必定产生变化，为了研究这一变化，用拍摄录像的方法来记录这一动态过程，然后将摄录的影片传到计算中，用播放器播放影片，选择合适的时间间隔，采用人工处理方法处理数据.

2.2.2 人工计数法

取自动扶梯水平梯级为分析断面，记录每P个人通过该断面的时间Δt.广州地铁体育西路站自动扶梯运行速度为0.65 m/s，倾斜角度为30°.由图1可知水平方向的速度为

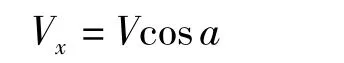
则Δt时间内水平方向上的行走距离L为

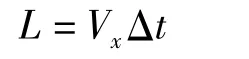
Δt时间内的扶梯行走区域的面积S为

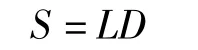
其中:D为断面宽度，此次观测断面处扶梯梯级宽度为1m，扶手间公称宽度为1.2m，考虑行人生理尺寸特点，取D=1.2m.

密度K为

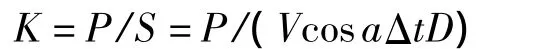
流量Q为

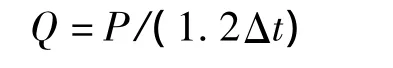
3 自动扶梯入口段交通基本图及特性分析

图2、图3为扶梯入口段流量－密度、速度－密度图.需要说明的是，由于本次录像实验只拍摄行人下车涌向自动扶梯的情景，因此，没有密度K＜0.68人/m2的数据.

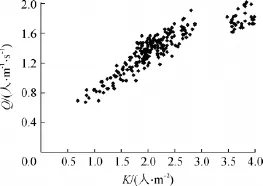
图2 扶梯入口段流量－密度图Fig.2 Diagram of escalator entrance's flow-density

从图2可看出，流量随着密度的增加呈上升趋势，但表现出明显的阈值现象，没有数据点落入K∈(2.87，3.48)人/m2的区间，具体分析如下:

K＜2.87人/m2时，流量随着密度的增加而迅速增加，变化趋势非常明显，这是由于密度较小时，行人运动空间充足，随着密度的增加，通过观测断面的人数也就在增加，处理这部分数据并拟合，结果如图4所示，得到相关系数为0.86，这说明在扶梯入口段，密度变化对流量的影响较大.

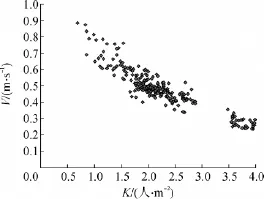
图3 扶梯入口段速度－密度图Fig.3 Diagram of escalator entrance's velocity-density

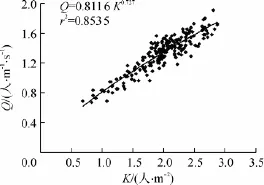
图4 K＜2.87人/m2时的扶梯入口段流量－密度图Fig.4 Diagram of escalator entrance's flow-density，K ＜ 2.87人/m2

K＞3.48人/m2时，流量随着密度的增加不再增加，而是趋于平衡.这是由于当密度较大时，人群发生拥挤，穿行变得困难，行走速度明显下降，流量在某个较大值附近波动.因此拐点处的流量值即为扶梯入口段的最大通行能力，由于扶梯上的人流来自扶梯入口，因此这个最大值将限制自动扶梯的实际载客能力，由图2可知，入口处最大通行能力为8727人/h，即扶梯的实际最大载客能力不会超过8727人/h.

K∈(2.87，3.48)人/m2时，没有数据点落入该区间，表现出明显的分层现象，可以用能级跃迁理论来解释，即高能级的粒子在某种激发下，跃迁到低能级上.具体表现为，随着入口段密度的增加，行人间的间距逐渐缩小，为了满足心理距离行人间不会太过于紧贴在一起，限制了后续行人的行为，因此密度不会超过某值;后续行人因等待产生焦虑，开始向前推挤，挤入扶梯入口段，将入口段的拥挤平衡状态打破，密度突然增加.此处行人间的推挤就是发生能级跃迁的激发.

从图3不难看出，随着密度的增加，速度整体上处于下降趋势.但不同密度区间内，速度下降的趋势不同，具体表现如下.

K＜2.87人/m2时，速度随密度的增加迅速下降，这说明密度增加对速度影响较大，对这部分的数据分析拟合如图5所示，得到相关系数r2为0.782;

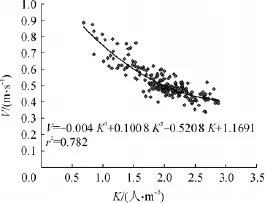
图5 K＜2.87人/m2时的扶梯入口段速度－密度图Fig.5 Diagram of escalator entrance's velocity-density，K ＜2.87人/m2

K＞3.48人/m2时，速度基本维持在0.25 m/s附近，这是因为观测区的出口即为自动扶梯的活动梯级，该梯级始终以定速输送人流，因此整个分析过程中始终有人流被运走，不会出现行人在扶梯入口段停滞不前的现象，即速度不会降到0.

K∈(2.87，3.48)人/m2时，没有数据点落入该区间，分析同流量－密度关系.

4 自动扶梯段交通基本图及特性分析

自动扶梯的实际载客能力与扶梯梯级宽度密切相关，实测数据所得到的基本图为梯级宽度等于1m时的自动扶梯基本图.

处理人工记录的数据，得到自动扶梯梯级上行的流量－密度，速度－密度图如图6、7所示.由图6可以看出，扶梯梯级上的行人流量随密度的增加而呈线性增加，但扶梯梯级密度最大没有超过4人/m2，这是因为:

取10个梯级(宽1m，深0.4m)为一个区，则该区面积为

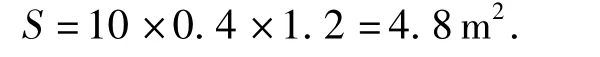
该区最大人数为(假定每个梯级站两人):

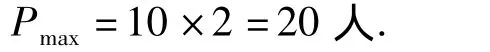
则最大密度为

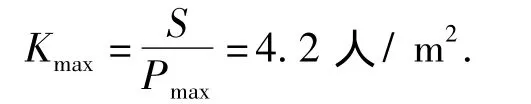
在笔者的实际观测中，一个梯级很少同时站立两个人，且由于人的心理空间，相邻梯级很少会同时被占用，因此密度不会达到理论值4.2人/m2.由图6可以得出扶梯上流量最大值为8655人/h，满足扶梯入口交通特性对扶梯实际载客能力的限制作用，按照地铁标准该站扶梯的理论载客能力为9600人/h，因此该实际最大载客能力为理论值的90%［15］.

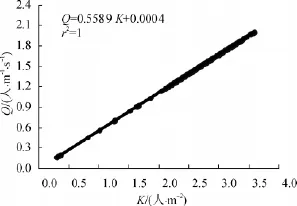
图6 扶梯段流量－密度图Fig.6 Diagram of escalator's flow-density

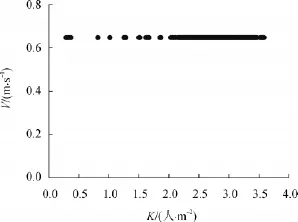
图7 扶梯段速度－密度图Fig.7 Diagram of escalator's velocity-density

5 结论

通过对广州地铁自动扶梯的实验调查，建立了梯级宽度为1m的自动扶梯入口段与自动扶梯段行人的流量－密度图和速度－密度图，并用能级跃迁的观念简单解释了图中的分层现象.给经分析得知，流量随密度的增加而增加，当密度增加到某一阈值时，流量在阈值对应处波动，这一阈值对应的流量值即为实际载客能力，扶梯入口段速度随密度的增加而减小，但速度不会减小到0，因为扶梯总是以定速输送人流，入口处不会出现行人停滞不前的现象.扶梯上的流量随密度的增加而线性增加，由于密度受扶梯宽度的影响导致密度不会超过4.2人/m2.本次试验入口处流量最大值为8727人/h，自动扶梯上的实际载客能力为8655人/h，为理论值载客能力的90%.

［1］王炜.交通工程学［M］.南京:东南大学出版社，2000:125.

［2］GB16899—1997.自动扶梯和自动人行道的制造与安装安全规范［S］.

［3］Paul Davis，Dutta Goutam.Estimating of capacity of escalators in London underground［EB/OL］.［2010-10-25］.http:∥ www.iimahd.ernet.in/publications/data/2002-11-01GoutamDutta.pdf/.

［4］Fruin.Pedestrian planning and design［M］.［S.l.］:Elevator Woddlnc，1987.

［5］Portland State University.Stop，station，and terminal capacity［EB/OL］.［2010-10-25］.http:∥web.pdx.edu/～ bertini/courses/558/Stop-Station-Terminal.pdf/.

［6］Tobias Kretz，Anna Grunebohm，Andreas Kessel，et al.Upstairs walking speed distributions on a long stairway［J］.Safety Science，2008(46):72-78.

［7］Taku Fujiyama，Nick Tyler.Pedestrian speeds on stairs-an initial step for a simulation model［C］∥Proceedings of 36th Universities Transport Studies Group Conference.UK:Life Science Centre，2004.

［8］Daly.Pedestrian speed-flow relationship for underground stations［J］.Traffic Engineering and Control，1991，32(2):75-77.

［9］田晨.影响自动扶梯运力的非技术因素的综合分析［J］.起重运输机械，2005(4):17-20.Tian Cheng.Comprehensive analysis of escalator capacity in non-technical factors［J］.Hoisting and Conveying Machinery，2005(4):17-20.

［10］田晨.自动扶梯运力的非技术因素分析［J］.环保与节能，2004(7):48-50.Tian Cheng.Analysis of escalator capacity in non-technical factors［J］.Energy Conservation and Environmental Protection，2004(7):48-50.

［11］陈峰，吴奇兵，张慧慧，等.北京地铁1号线车站设施与客流关系分析［J］.交通运输系统工程与信息，2009，9(2):93-98.Chen Feng，Wu Qi-bing，Zhang Hui-hui，et al.Relationship analysis on station capacity and passenger flow:a case of Beijing subway line1［J］.Transportation Systems Engineering and Information Technology，2009，9(2):93-98.

［12］李三兵，陈峰，李程垒.对地铁站台集散区客流密度与行进速度的关系探讨［J］.城市轨道交通研究，2009(12):34-41.Li San-bing，Chen Feng，Li Cheng-lei.Passages'density and travel speed at subway stations［J］.Urban Mass Transit，2009(12):34-41.

［13］柳伍生，余朝玮.地铁站楼梯行人流交通特征的数据拟合分析［J］.计算机工程与应用，2008，44(3):50-52.Liu Wu-sheng，Yu Zhao-wei.Analyzing to characteristics of pedestrians flow on stairways at metro transfer stations basing on data fitting［J］.Computer Engineering and Applications，2008，44(3):50-52.

［14］王凯英，廖敏军，孟宪强，等.上海地铁站内行人楼梯交通特性［J］.上海海事大学学报，2009，30(1):69-73.Wang Kai-ying，Liao Min-jun，Meng Xian-qiang，et al.Stair traffic characteristics of underground station in Shanghai［J］.Journal of Shanghai Maritime University，2009，30(1):69-73.

［15］GB 50157—2003.地铁设计规范［S］.