基于泛函灵敏度方法的PSS参数优化设计*

薛振宇 房大中 袁世强

(1.天津大学电力系统仿真控制教育部重点实验室，天津300072;2.天津市电力公司技术中心，天津300022)

现代电力系统的迅速发展，形成远距离重负荷输电的大区互联电网，因此由系统扰动所引发的低频振荡问题日趋严重［1-2］.在励磁系统上加装电力系统稳定器(PSS)是抑制低频振荡经济有效的措施之一［1］.但在多机电力系统环境中，PSS的控制策略多数是基于部分发电机的分散控制，导致系统中PSS间经常因缺乏协调而不能有效抑制低频振荡的发生［3］.另外，基于特征根分析的PSS参数设计方法，在线性化过程中忽略了泰勒级数展开式的高阶项而不能考虑电力系统的非线性对稳定性控制的不利影响.研究表明传统的PSS参数设计有时会对系统的暂态稳定性造成负面影响［4］.

多年来，学术界对PSS参数配置问题进行了深入的研究.文献［5］中提出了PSS协调控制的一种梯度法，由于寻优策略是局部的，因此计算结果不是全局最优.文献［6］中提出了对两个目标函数同时进行优化的PSS参数配置方法，该方法因其操作困难而往往存在收敛问题.文献［7］和文献［8］中分别采用多尺度随机模拟算法和模拟退火算法进行PSS参数整定，该类方法首先确保系统的最小阻尼比满足预设的限值，再通过时域仿真以校验PSS大扰动情况下的阻尼控制效果.文献［9-11］中研究了PSS和励磁调节器的相互配合问题，提出了通过采用不同结构的附加断续励磁控制来进一步改善系统的暂态稳定性.

文中提出了一种PSS参数协调优化的共轭梯度法.该方法的特点是:引入了一种系统动态组合泛函指标来评价PSS阻尼功率振荡的效果;以该组合泛函指标最小作为PSS参数优化模型的目标函数;采用变分法，发展了计算该组合泛函指标对PSS参数梯度的轨迹逆积分方法.由于目标函数考虑了电力系统的非线性特征，该方法不但可提高系统的小扰动稳定性，同时也可以有效地阻尼大扰动引起的功率振荡.此外，通过IEEE四机双区域和IEEE十机新英格兰测试系统的算例说明了文中PSS参数协调配置方法的有效性.

1 电力系统数学模型

1.1 励磁系统及PSS模型

文中采用如图1所示的快速励磁系统和PSS［2］.Efd和 Vs分别为励磁系统和 PSS 的输出信号;机端电压Vt和发电机角速度偏差Δω分别为励磁系统和PSS的输入信号;Vref为励磁系统的参考电压.图中所有变量和参数均为标幺值.

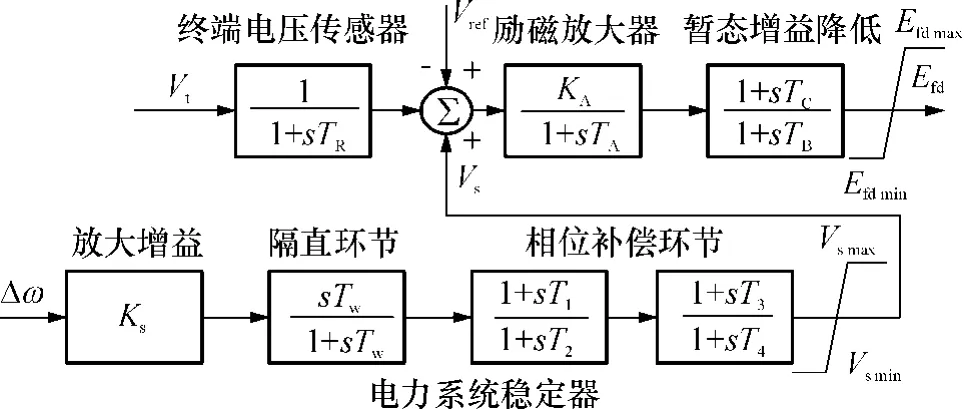
图1 励磁系统及PSS结构框图Fig.1 Block diagram of the excitation system and PSS

图中参数的典型取值为:TR=0.01，KA=200，TA=0.015，TB=10，TC=1;Tw为 PSS 隔直环节的时间常数，Tw=10，T2、T4为 PSS滞后时间常数，T2=0.05，T4=0.05;PSS的增益系数Ks(取值范围为［0.01，30.00］)和PSS超前环节的时间常数 T1与T3(取值范围为［0.01，5.00］)为待优化参数.

1.2 电力系统暂态模型

通常，故障中和故障后的电力系统的动态过程可用如下微分－代数方程组来表示

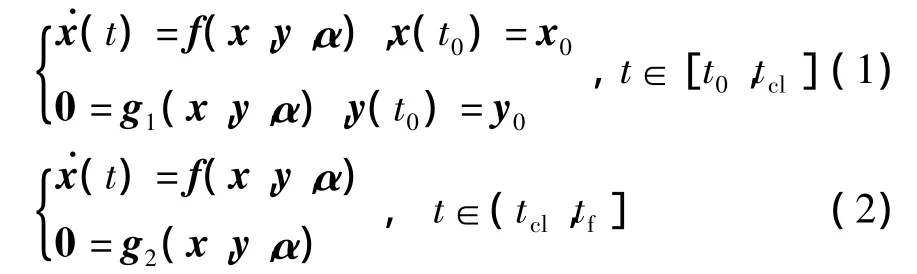
式中:向量x表示状态变量;y表示代数变量，初值条件由稳态运行方式给定;向量α由所有PSS的待优化参数组成.表示微分方程的向量函数f(·)描述同步发电机、励磁控制系统及其PSS的动态特性;向量函数g1(·)和g2(·)分别描述系统故障中和故障后的代数方程;t0和tcl分别表示大扰动故障的起始时刻和故障消除时刻;tf为系统仿真的终止时刻(即观察系统动态行为的终止时刻).

2 PSS参数优化方法

2.1 PSS参数优化问题模型

理想PSS应能有效地抑制系统低频振荡发生.因此PSS参数的协调优化，需要同时满足两个条件:对区域内或区域间功率振荡模式的阻尼比满足工程要求［12-15］，以有效地阻止小扰动引发的稳定性问题;对大扰动后系统的功率振荡提供充分的阻尼.

为了更好地评估系统功率振荡的衰减程度，文中采用系统发电机的振荡角频率来定义PSS阻尼效果的组合泛函指标J如下:

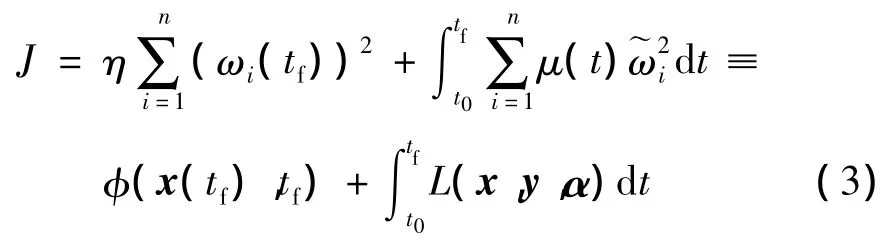
式中:n为系统发电机数目;ωi(tf)为发电机i在tf时刻相对于同步转速的角速度;˜ωi为发电机i相对于系统惯性中心的角速度，显然系统大扰动后J越小PSS阻尼系统功率振荡的效果越好;η和μ(t)为权重系数，用以协调末值泛函和积分泛函在评价指标中的权重.为突出PSS对系统前几次功率振荡的阻尼效果，可令μ(t)为一个随时间衰减的函数，如μ(t)=e－t，与其对应的权重系数为 η =20.式(3)右边第1项和第2项分别为电力系统时段［t0，tf］动态过程的末值泛函和积分泛函，于是以J为目标函数的PSS参数优化模型如下式所示.

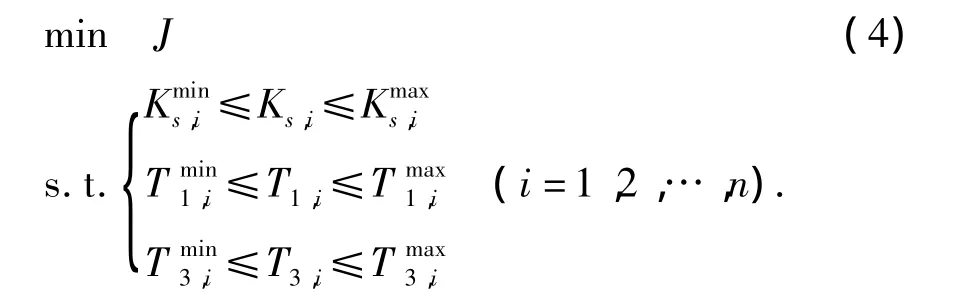
式中:约束条件中的各个变量含义如图1所示，对应的上标max、min分别表示相应PSS优化参数的上限和下限.

2.2 组合泛函指标梯度的逆积分算法

引入时变的拉格朗日乘子向量λ(t)和ξ(t)［13］，考虑式(1)、式(2)和式(3)，组合泛函指标J可表示为

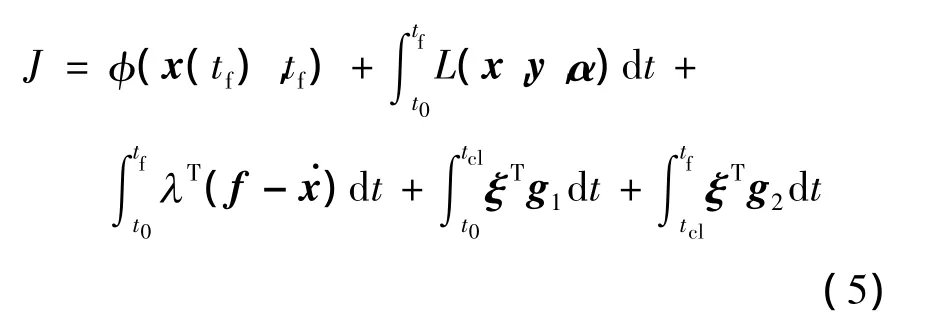
对该式两端进行变分操作［14］，可以证明只要拉格朗日乘子向量λ(t)和ξ(t)满足式(6)－(8)，便可用式(9)计算组合泛函指标J对参数向量α的梯度.

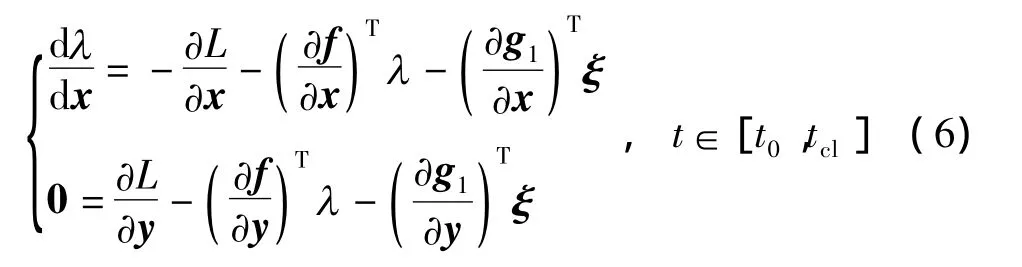
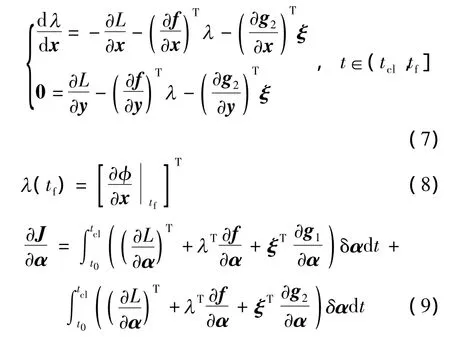
式(9)表明，计算组合泛函指标J对PSS优化参数α的梯度需获得各离散时刻被积函数的值.考虑式(3)目标函数J及函数g1(·)和g2(·)皆不显式地包含PSS优化参数α，因此有

将式(10)代入式(9)可得最终的梯度计算表达式如下:

根据上述推导结果，计算指标J梯度的轨迹逆积分方法步骤可简述如下.

(1)用系统(1)和(2)对某一典型大扰动进行数值仿真，获得时段［t0，tf］内各离散时刻x和y的数值解.

(2)用式(9)计算λ(tf).

(3)逆时间轴从tf时刻至t0时刻对时变线性系统(7)和(6)进行数值积分，计算各离散时刻的λ(t).

(4)将各离散时刻的λ(t)代入式(11)计算梯度.

上述算法需要逆时间轴积分计算拉格朗日乘子向量λ(t)，因此称其为组合泛函指标梯度的轨迹逆积分算法.

2.3 PSS参数优化的共轭梯度法

借助于组合泛函指标梯度的计算，文中采用共轭梯度法求解PSS参数优化问题(4).共轭梯度法适用于求解大规模非线性规划问题，且具有较好的收敛性.图2为文中提出的共轭梯度法的算法流程.图中，g≡∂J/∂α代表指标J对PSS参数α的梯度;γ和β为计算过程中的中间变量.

图2中，符号i表示迭代次数;ε表示收敛判断的精度，通常取ε=10－6;s表示搜索方向;γ表示采用黄金分割法计算得到的最优步长;β表示计算的中间参数，并通过β来确定新的搜索方向。当梯度g满足收敛的判断要求时，即可认为PSS待优化参数达到了局部最优，退出计算.

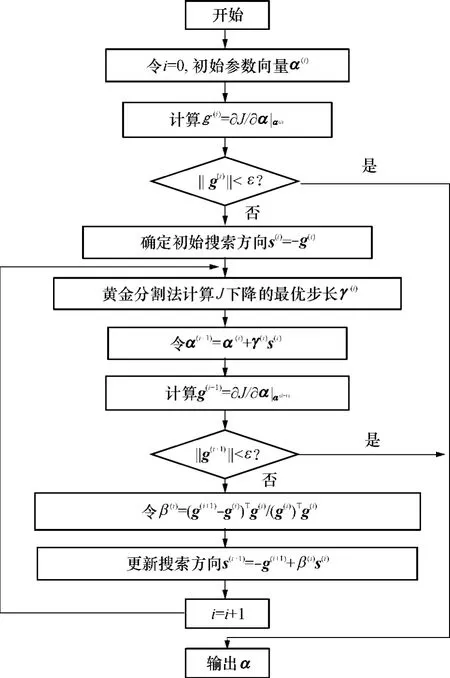
图2 共轭梯度法求解优化模型的流程图Fig.2 Flow chart of the conjugate gradient method for solving optimization model

3 算例分析

3.1 四机双区域测试系统算例

图3为四机双区域测试系统的结构图，系统参数见文献［2］.算例中所有4台发电机G1－G4均采用暂态双轴模型，并配有图1所示励磁及PSS控制系统，其信号Efd和Vs的上下限分别为 ±5(p.u.)和±0.2(p.u.).

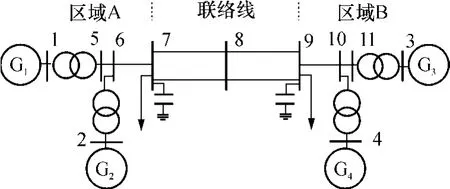
图3 四机双区测试系统Fig.3 4-generator 2-area test system

参数优化采用的预想故障为母线8在0.5 s发生三相短路故障，故障持续6周波后自动消除.PSS的初始配置如表1第2行所示，优化后的PSS参数如表1第4行至第7行所示，第3行为文献［9］优化后所得的PSS参数.为检验PSS参数优化的效果，绘制了某故障后对应3种PSS参数的功角θi(相对于惯性中心)摇摆曲线见图4.图4表明文中算法设计的PSS可以有效地阻尼系统大扰动后的振荡，故障后系统发电机功角曲线的摇摆幅度较小，并能够迅速衰减.其他系统故障仿真所得的结论与图4类似.

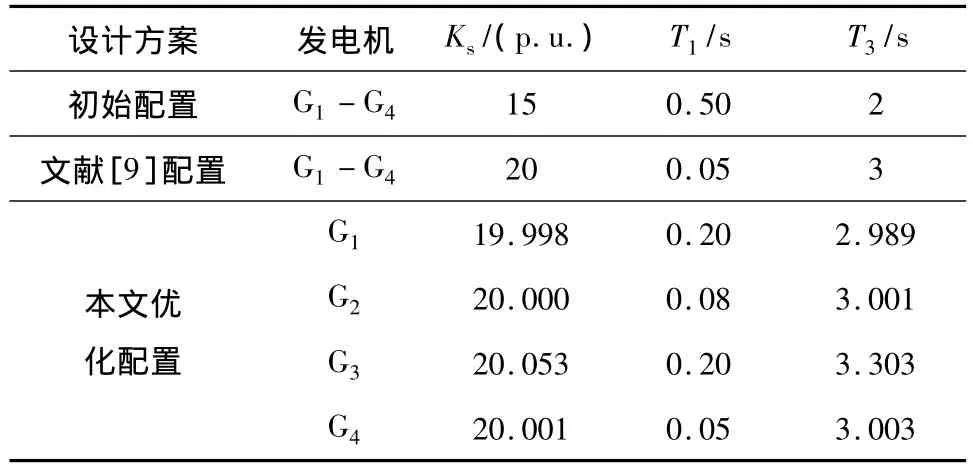
表1 四机双区测试系统的PSS参数Table 1 PSS parameters of the 4-generator 2-area test system

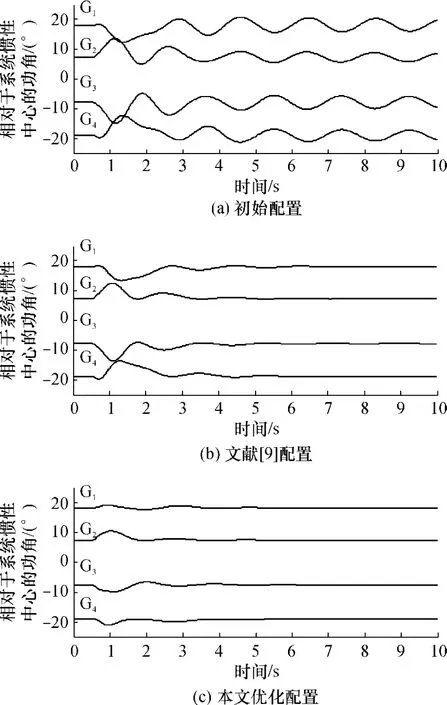
图4 四机双区域测试系统的功角摇摆曲线Fig.4 Swing curves of the 4-generator 2-area test system

表2列出了3种PSS配置下系统机电模式特征根及与其对应的阻尼比和自然振荡频率，通过对比可见:对于系统局部模态(即A区(G1对G2)和B区(G3对G4)的振荡模式)，文中算法所得的阻尼比较前两者有明显的提高;对于区域模态(即A区对B区的振荡模式)，文中算法所得的阻尼也是最好的.

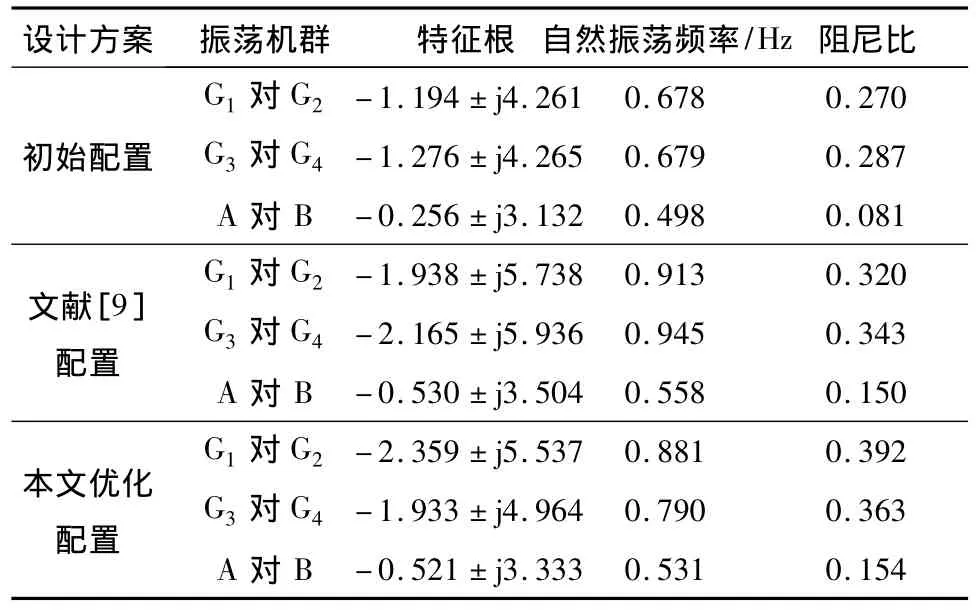
表2 四机双区测试系统机电模式特征值比较Table 2 Comparison in terms of eigenvalue of electromechanical modes for the 4-generator 2-area test system

3.2 IEEE十机新英格兰测试系统算例

IEEE十机新英格兰测试系统的结构如图5所示，系统参数见文献［9］.算例中，所有发电机采用与4机系统相同的发电机模型及图1所示的励磁与PSS，其信号 Efd和 Vs的上下限分别为 ±5(p.u.)和±0.2(p.u.);负荷由40%恒阻抗模型与60%恒功率模型组成.

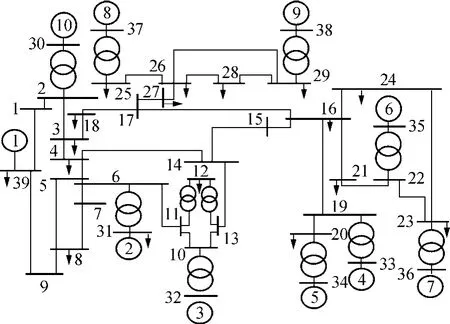
图5 十机新英格兰测试系统Fig.5 10-generator New England test system

参数优化采用的预想故障为5号母线三相短路，6个周波后故障自行清除，各PSS初始配置参数(p.u.):Ks=20，T1=0.5，T3=0.2.优化后的 PSS参数见表3.

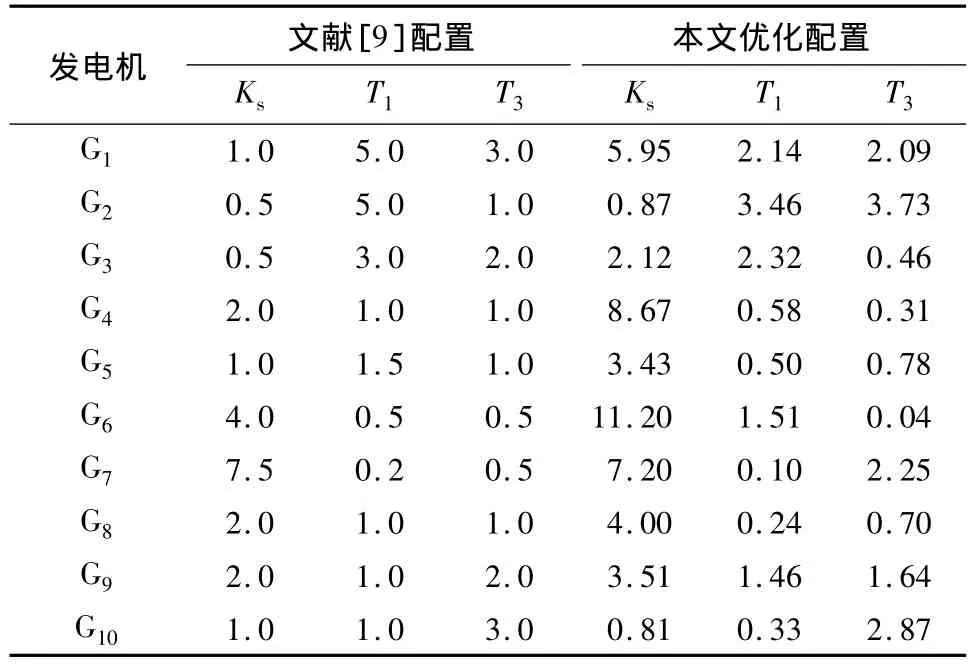
表3 优化设计后十机新英格兰测试系统的PSS参数Table 3 Optimized PSS parameters of the 10-generator New England test system

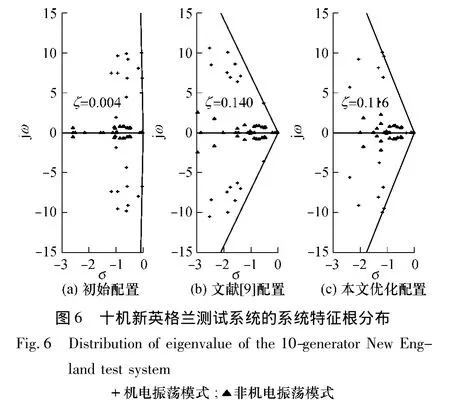
图6给出了优化后、初始配置及文献［9］三组PSS参数下系统特征根的分布情况.jω为特征根虚部，σ为特征根实部.由图6可见，初始PSS配置条件下的系统阻尼严重不足，最小阻尼比ζ=0.004;文献［9］PSS配置下，系统的最小阻尼比最好;文中所得的PSS参数使得系统最小阻尼比有很大程度的提高.

为检验PSS参数优化的效果，绘制了某故障后对应3种PSS参数的功角(相对于惯性中心)摇摆曲线，见图7.其中图7(a)表明，系统大扰动后出现明显的功率振荡现象.图7(b)和(c)表明，虽然文献［9］所给PSS方案其阻尼比最理想，但在阻尼大扰动后功角振荡方面不如文中方法设计的PSS参数.文中设计的PSS参数可使系统振荡迅速衰减，仅经过一个摇摆后，系统便趋于稳定.在十机新英格兰测试系统上其它大扰动仿真结果与图7类似.

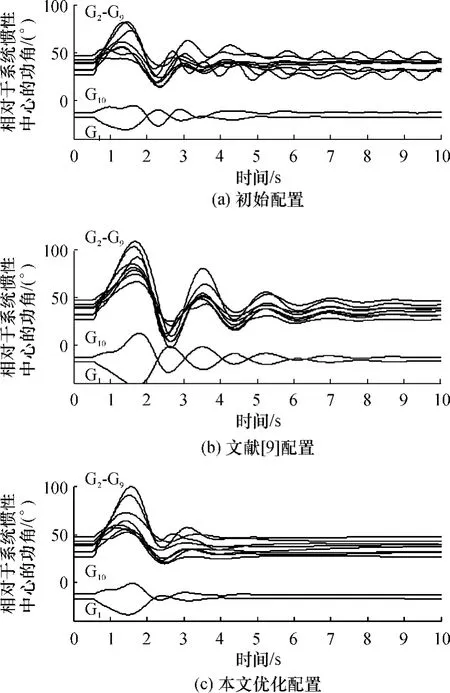
图7 某大扰动后十机新英格兰测试系统的功角摇摆曲线Fig.7 Swing curves after a big disturbance on the 10-generator New England test system

4 结语

文中提出一种以组合泛函指标最小为目标函数的PSS参数优化模型.发展了采用变分法计算组合泛函指标对PSS参数梯度的轨迹逆积分算法.在IEEE四机双区域和IEEE十机新英格兰测试系统上的算例分析表明，文中方法所设计的PSS参数配置方案能够同时较好地提高系统的小干扰稳定性和大干扰稳定性.

［1］王铁强，贺仁睦，王卫国，等.电力系统低频振荡机理的研究［J］.中国电机工程学报，2002，22(2):21-25.Wang Tie-qiang，He Ren-mu，Wang Wei-guo，et al.The mechanism study of low frequency oscillation in power system ［J］.Proceedings of the CSEE，2002，22(2):21-25.

［2］Kundar P.Power system stability and control［M］.New York:McGraw-Hill，1994.

［3］Zhang P，Coonick A H.Coordinated synthesis of PSS parameters in multi-machine power systems using the me-thod of inequalities applied to genetic algorithms［J］.IEEE Transudations on Power Systems，2000，15(2):811-816.

［4］Lin C M，Vittal V，Kliemann W，et al.Investigation of modal interaction and its effects on control performance in stressed power systems using normal forms of vector fields［J］.IEEE Trans on Power Systems，1996，11(2):781-787.

［5］Hong Ying-yi，Wu Wen-ching.A new approach using optimization for tuning parameters of power system stabilizers［J］.IEEE Trans on Energy Conversion，1999，14(3):780-788.

［6］Abdel-Magid Y L，Abido M A，Al-Baiyat S，et al.Simultaneous stabilization of multimachine power systems via genetic algorithms ［J］.IEEE Trans on Power Systems.1999，14(4):1428-1439.

［7］Fang D Z，Yuan S Q，Wang Y J，et al.Coordinated parameter design of STATCOM stabilizer and PSS using MSSA algorithm［J］.IET Generation，Transmission and Distribution，2007，1(4):670-678.

［8］Abido M A.Pole placement technique for PSS and TCSC-based stabilizer design using simulated annealing［J］.Electrical Power and Energy Systems，2000，22(8):543-554.

［9］IEEE.Stardard datas［EB/OL］.［2010-01-09］.http:∥psdyn.ece.wisc.edu/IEEE_benchmarks/index.htm.

［10］Harley R G，deMeillon T A，Janischewskyj W.The transient stabilization of a synchronous machine by discontinuous supplementary excitation control［J］.IEEE Transactions on Power Apparatus and Systems，1985，PAS-104(6):1394-1399.

［11］Chaudhuri B，Majumder R，Pal B C.Application of multiple-model adaptive control strategy for robust damping of inter-area oscillations in power systems［J］.IEEE Transactions on Power Systems，2004，12(5):727-736.

［12］Graham Rogers.Power system oscillation［M］.［S.l.］:Kluwer Academic Publishers，2000.

［13］胡寿松，王执铨，胡维礼.最优控制理论与系统:第二版［M］.北京:科学出版社，2005.

［14］Fang D Z，Xiaodong Y，Jingqiang S，et al.An optimal generation rescheduling approach for transient stability enhancement［J］.IEEE Transactions on Power Systems，2007，22(1):386-394.

［15］刘红超，雷宪章，李兴源，等.互联电力系统中PSS的全局协调优化［J］.电网技术，2006，30(8):1-6.Liu Hong-chao，Lei Xian-zhang，Li Xing-yuan，et al.Global coordinated optimization of PSSs in interconnected power systems［J］.Power System Technology，2006，30(8):1-6.