制造决策的知识融合粗糙集模型*

徐晓 翟敬梅 刘海涛 康博

(华南理工大学机械与汽车工程学院，广东广州510640)

信息技术的迅速发展及其与制造业的融合，使制造日益走向数字化.制造信息在制造活动中具有知情、累积、转化、物化、知化、决策的作用，对制造企业成功运作至关重要［1］.近10来年，各种数据挖掘技术在机械制造领域的应用得到了广泛的关注和研究［2-5］.制造过程具有很大程度上的不确定性［6］，现实生产中获取的制造过程信息往往是不完备的，粗糙集理论作为一种有效分析不一致、不完整信息的数据挖掘工具，近几年在制造决策等方面得到了较深入的研究［7-9］.

粗糙集理论特点是处理数据时不需要关于数据的任何先验或附加信息，获取知识的确定程度主要取决于信息的完备性.而实际上，我们或多或少掌握一些领域的知识和经验，一方面，这些知识和经验在一定程度上可以弥补一些信息的不足，提高决策的确定性，另一方面，在数据挖掘过程中遵循这些知识和经验，可以提高决策的准确性.文中将知识融入到粗糙集模型中，在传统粗糙集(ORSM)以不可分辨关系处理数据的基础上，对知识进行建模，将知识映射为函数关系，建立一个基于不可分辨-函数关系的综合分析信息和知识的新型粗糙集模型，即知识融合粗糙集模型(KBRSM).

1 知识的粗糙集表示

制造过程中影响产品的生产因素是复杂的，各种参数之间的非确定型关系大量存在，往往很难建立精确的函数关系，然而就某单一生产参数而言，其对生产的影响趋势易于通过实验或经验获得.

变量x、y有函数关系y=F(x)，x在其定义域内任意两值 x1、x2，有 x1＞ x2，如果 F(x1)＞ F(x2)，则x和y有正函数关系，表示为FUN;如果F(x1)＜F(x2)，则x和y有反函数关系，表示为FUN;如果F(x1)=F(x2)，则x和y有等效函数关系，表示为;如果F(x1)≥F(x2)，则 x和 y有正 -等效函数关系，表示为;如果 F(x1)≤F(x2)，则x和y有反-等效函数关系，表示为.

粗糙集中，决策表(简称 DT)S={U，X∪y，V，f}，U是对象集合，X∪y是属性集合，V是属性值的集合，f是一个信息函数，它指定U中每一对象的属性值，如fxi(uj)表示对象uj(uj∈U)在属性xi(xi∈X)上的取值.若条件属性xi与决策属性y有函数关系，定义:

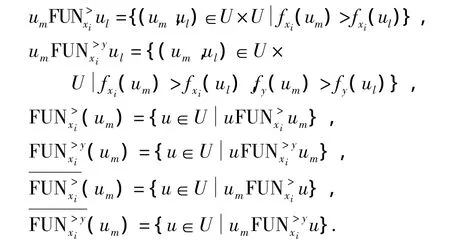
2 知识融合的粗糙集模型

将知识融合到粗糙集模型，知识表征为函数关系，所得KBRSM为基于“不可分辨-函数关系”的扩展粗糙集模型.

1)不可分辨-函数关系.

S={U，X∪y，V，f}，X={x1，x2，…，xi，…，xN}，X'={x1，…，xi-1，xi+1，…xN}，xi与 y 有函数关系

与对象um(um∈U)关于X和y的不可分辨-正函数关系集合为:

与对象um关于X和y的不可分辨-正函数关系集合为:

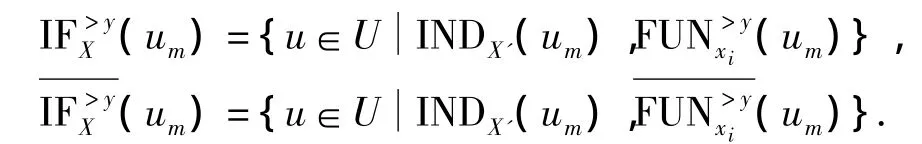
INDX'(um)表示与对象um关于X'的不可分辨关系的集合［10］.

2)上、下近似集.

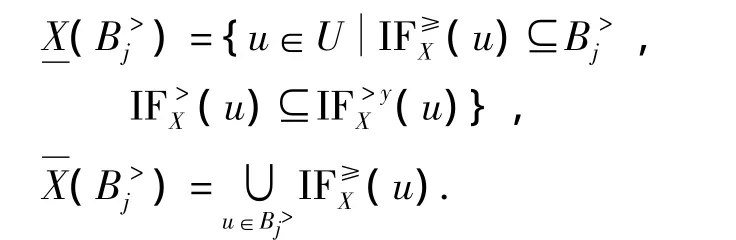
类似地，条件属性X关于决策分类B＜j的上、下近似集分别为:

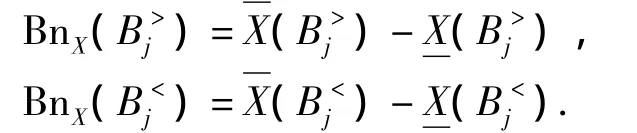
3)近似质量.

条件属性X关于决策属性y的近似质量为:

式中，Card()表示集合中对象的个数.很明显，0≤γX(y)≤1，如果γX(y)=1，U关于条件属性X和决策属性y是一个精确集;如果 γX(y)＜1，则U关于条件属性X和决策属性y是一个粗糙集.

一个决策表 S={U，{x1，x2，x3}∪y，V，f}见表1，已知x1与y呈正比变化，即有函数关系根据ORSM，有γX(y)=1，表明决策表中各对象是一致和协调的.根据KBRSM，有，表明有不一致、不协调的对象出现.观察对象2和3，从条件属性来判断，它们在属性x2和x3上取值相同，在属性x1上，对象3的值大于对象2的值，根据已有的知识，对象3的y值不应小于对象2的y值，因此对象2和3是不一致和不协调的，这种不一致是由于违反了已知的函数关系，如果忽略了这个知识，这种不一致是不能发现的.因此，KBRSM具有更高的划分精度，获取的规则更为精确.

表1 决策表Table 1 A decision table

4)简约和核.

若存在X1⊂X，满足 γX1(y)=γX(y)且不存在X2⊂X1使 γX2(y)=γX(y)，称 X1为 X 的一个属性简约，用Redy(X)表示，核Corey(X)=∩Redy(X).

5)规则获取.

X={x1，x2，…，xi，…，xN}是决策表 S 的一个属性简约集，xi∈X与决策属性y有函数关系对象us和ut(us∈U，ut∈U)关于X有不可分辨-函数关系，且根据KBRSM，可获取以下不同结构形式的规则:

(1)“=”形式规则.

如果 fx1(u)=A1，A2，…，fxi(u)=，…，fxN(u)=AN，则 fy(u)=Bs.

如果 fx1(u)=A1，A2，…，fxi(u)=，…，fxN(u)=AN，则 fy(u)=Bt.

(2)“＞”形式规则.

如果 fx1(u)=A1，A2，…，fxi(u)＞，…，fxN(u)=AN，则 fy(u)＞ Bt.

(3)“＜”形式规则.

如果 fx1(u)=A1，A2，…，fxi(u)＜，…，fxN(u)=AN，则 fy(u)＜ Bs.

(4)“＞＜”形式规则.

如果 fx1(u)=A1，A2，…，＜fxi(u)＜，…，fxN(u)=AN，则 Bt＜fy(u)＜Bs.

另外，第1类规则分别与第2、第3和第4类结构形式规则组合，分别可以得到“≥”、“≤”和“≥≤”形式的规则.

因此，KBRSM在知识的获取上，内容和结构形式更丰富，更灵活，句子结构更具概括性和归纳性.

3 KBRSM在制造质量决策应用

表2为一个轴(φ50mm×300mm，45钢)加工过程中得到的31个加工信息，决策表为S={U，X∪y2，V，f}，其中 X={y1，x1，x2，x3，x4}，切削速度 x1、进给量x2和切削深度x3为该加工过程的输入参数，x4表征加工过程中刀具的状态，分为“正常”和“异常”，状态值由图1所示刀具状态在线监测系统获得.

图1 刀具状态监测系统Fig.1 Tool condition monitoring system

刀具上的主切削力Fz与刀具磨损的相关性较强，受外界环境影响不大.研究发现，对于切削45钢这样的单一均质材料，其切削力动态分量信号随刀具磨损变化波动不是很明显，而且Fz波动的幅度和频率较为均衡，切削力的静态分量随着刀具磨损到一定程度，将会急剧增加.根据刀具磨损到不能正常工作时，平均切削力急剧增加这一特性，将主切削力静态部分即平均切削力作为切削过程中刀具磨损在线监测特征参量.

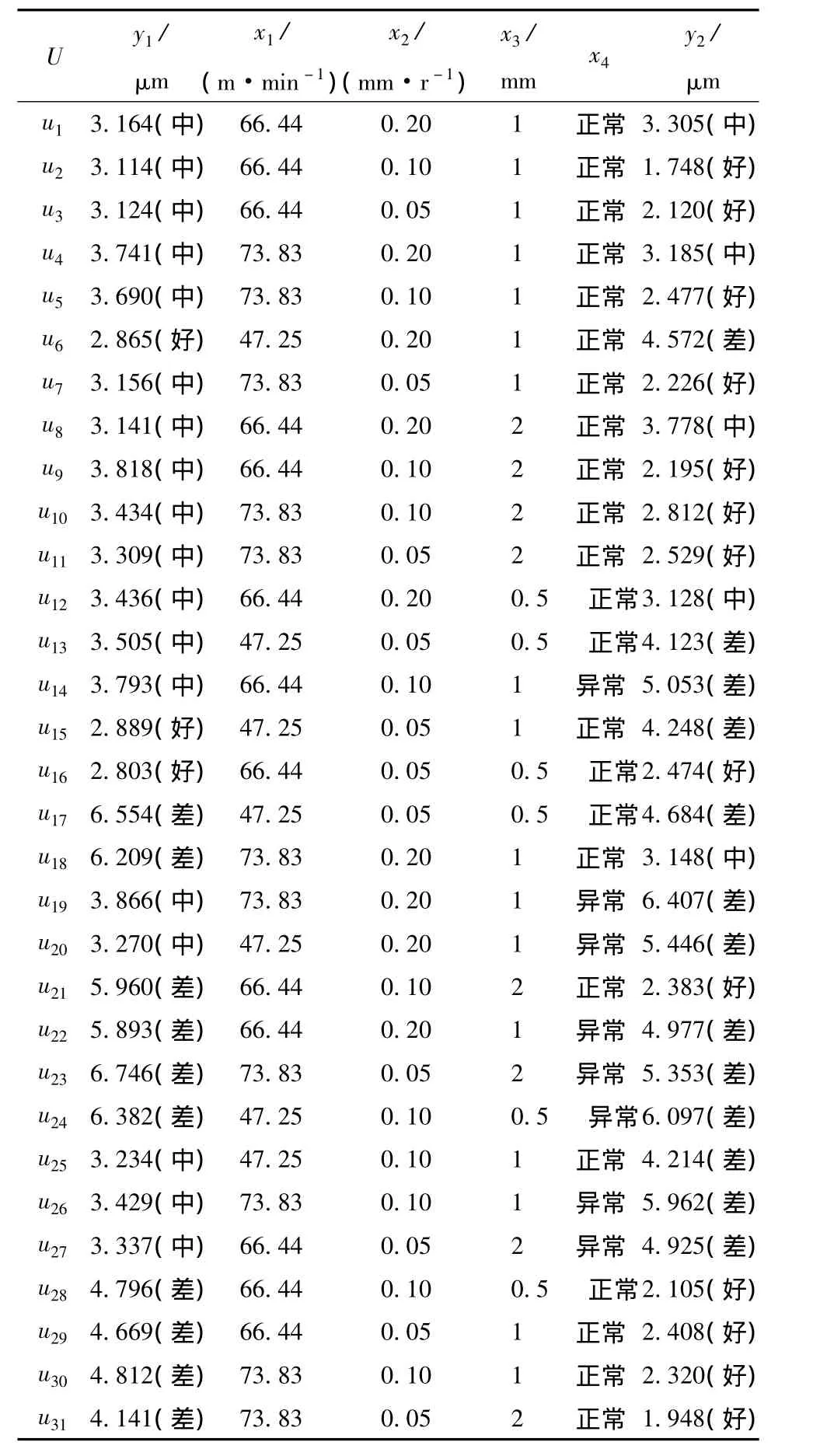
表2 轴生产加工决策表Table 2 DB with the examples of axis machining operation

图2(a)、(b)分别为加工表2中工件5(刀具正常)和26(刀具异常)时刀具Fz的采样曲线［11］.

在不同的切削条件下，刀具非正常工作的平均主切削力的临界值不同，刀具工作状态的正常与否通过基于神经网络的刀具在线监测系统获得［12］.

y1和y2表征工件加工后的表面粗糙度，y1为上道工序的加工质量，y2为本加工工序的质量，由TR200粗糙度测定仪测量.考虑到加工表面粗糙度数值的随机性，将该变量离散化，用“好”、“中”和“差”表示，分别对应“粗糙度 ＜3μm”、“3μm≤粗糙度≤4 μm”和“粗糙度 ＞4 μm”，质量值为“好 ＞中＞差”.

图2 加工工件的FzFig.2 Fzof cutting workpieces

根据知识和经验，条件属性y1与决策属性y2有函数关系，条件属性x2与决策属性y2有函数关系.

根据表2，可知决策分类:

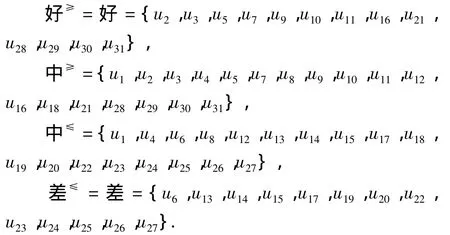
根据KBRSM，计算获得:

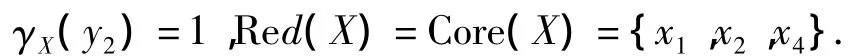
γX(y2)=1说明该决策表是一致的，获取的规则是确定的;Red(X)={x1，x2，x4}说明在该加工过程中，影响加工质量y2的生产因素是x1、x2和x4，属性y1和x3在其定义域范围内变化对质量y2无影响.

表3和表4分别列出了KBRSM和ORSM获取的决策规则.根据获取的规则可知造成质量较差的原因有两个:(1)刀具工作状态异常;(2)切削速度较低.要想获取一定满意程度的加工质量，必须在保持刀具正常的工作状态下，选择合适的工艺参数x1和x2.

表3 基于KBRSM获取的规则Table 3 Rules required by KBRSM

表4 基于ORSM获取的规则Table 4 Rules required by ORSM

相比之下，KBRSM获取规则蕴含的知识更丰富，适用范围更广.图3和图4分别描述了KBRSM和ORSM获取规则(当刀具处于正常状态下)的知识覆盖范围.图中的“*”对应表2中的加工对象，线或面上的任意点对应一条决策规则，两图直观地显示了KBRSM具有更广的适用性.

图3 基于KBRSM的适用范围Fig.3 Applicable coverage by KBRSM

表5对比了两组规则集所需的“规则数”和“条件数”，表明KBRSM获取的规则更简练、更具概括性，而且从规则中容易得到质量改进的策略和方法.

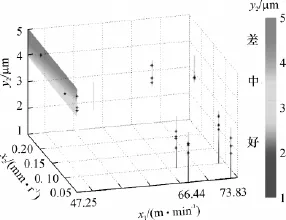
图4 基于ORSM的适用范围Fig.4 Applicable coverage by ORSM

表5 “规则数/条件数”的对比Table 5 Comparisons of number of rules/number of conditions

4 结语

制造过程是一个复杂、非线性、不确定的动态系统，现实中，制造过程信息和一定的领域知识越来越多.为此，文中提出了一种信息和知识集成的新型粗糙集模型，将知识映射为函数，通过建立已有知识的函数关系，构建了基于不可分辨-函数关系的知识融合粗糙集模型，解决了传统粗糙集无法处理知识的局限性.知识的嵌入是遵循已有知识对信息进行更高层次的挖掘，可以发现更精确、更丰富、适用性更广的决策知识.在规则的获取上，“=”、“＞”、“＜”和“＞＜”等结构形式更灵活，表达更简洁、更具归纳性.数据规模越大，已有知识越多，这些优势越显著.当知识愈加庞杂时，知识的有效组织和管理、挖掘算法效率等问题将是后续的研究工作.

［1］张伯鹏.制造信息全面质量管理研究［J］.制造业信息化，2002，24(8):1-5.Zhang Bo-peng.Investigation on TQM for manufacturing information ［J］.Manofacturing Automation，2002，24(8):1-5.

［2］Choudhary A，Harding J A，Tiwari M K.Data mining in manufacturing:a review based on the kind of knowledge［J］.Journal of Intelligent Manufacturing，2009，20(5):501-521.

［3］Andrew Kusiak，Matthew Smith.Data mining in design of products and production systems［J］.Annual Reviews in Control，2007，31(1):147-156.

［4］Massimo Pacellaa，Quirico Semerarob.Using recurrent neural networkstodetectchangesin autocorrelated processes for quality monitoring［J］.Computers＆ Industrial Engineering，2007，52(4):502-520.

［5］Yu Jian-bo，Xi Li-feng，Zhou Xiao-jun.Intelligent monitoring and diagnosis of manufacturing processes using an integrated approach of KBANN and GA［J］.Computers in Industry，2008，59(5):489-501.

［6］徐显龙，同淑荣，孙宜然，等.支持保质设计的制造质量信息模型［J］.制造业自动化，2008，30(7):14-17.Xu Xian-long，Tong Shu-rong，Sun Yi-ran，et al.Model of manufacturing quality information supporting design for quality［J］.Manufacturing Automation，2008，30(7):14-17.

［7］Tseng T L，Kwonb Y，Erteki Y M.Feature-based rule induction in machining operation using rough set theory for quality assurance ［J］.Robotics and Computer-Integrated Manufacturing，2005，21(6):559-567.

［8］殷国富，方辉，王卓，等.基于粗糙集的机械制造工艺知识发现方法研究 ［EB/OL］.［2010-12-10］.http:∥www.paper.edu.cn/index.php/default/releasepaper/content/200701-270.

［9］谢楠，李爱平，徐立云.面向可重组制造系统的快速诊断技术研究 ［J］.中国机械工程，2005，16(17-1):1545-1549.Xie Nan，Li Ai-ping，Xu Li-yun.Research on diagnosability technique for reconfigurable manufacturing system(RMS)［J］.China Mechanical Engineering，2005，16(17-1):1545-1549.

［10］胡寿松，何亚群.粗糙决策理论与应用［M］.北京:北京航空航天大学出版社，2006.

［11］翟敬梅.生产过程质量诊断与控制技术及其智能化决策支持系统的方法研究［D］.广州:华南理工大学机械工程学院，2003.

［12］李菊欢.基于分形理论和神经网络的刀具磨损在线监测［D］.广州:华南理工大学机械工程学院，2003.