基于最小势能原理的不规则零件排样算法*

刘虓 叶家玮 胡金鹏

(华南理工大学土木与交通学院，广东广州510640)

排样在造船、布匹和皮革加工业中有着广泛应用.排样效率的微小提升可带来巨大的经济效益，而排样算法属于组合优化问题，具有极高的计算复杂度，国内外对此进行了几十年持续不断的研究.大多数零件具有不规则的几何外形，因此其排样问题具有重大的现实意义.

目前不规则零件排样的求解策略主要基于两点:“靠左向下”原则(BL)和临界多边形(NFP).BL最初由Baker等［1］提出，由于其简便性和良好表现被广泛采用，同时一些改进算法也相继出现［2］.由于BL会在母板上形成孔洞，造成浪费，于是有学者提出“靠左向下并填充孔洞”求解策略(BLF)，其计算复杂度为 O(N3)(N 为零件数).Chazelle［3］则提出了一种改进的 BLF算法，其算法复杂度为O(N2).

由Art［4］首次提出的NFP是一种功能强大的几何工具，它与BL结合产生了各种排样算法［5］.不少学者对NFP进行了专门研究［6-7］.NFP的求解非常耗时，求解时间与零件数量N及零件的旋转角个数(RN)成平方关系.以欧洲排样研究组织(ESICUP)提供的标准问题SWIM(N=10，RN=2)为例，Burke等［7］声称每个NFP耗时1/66s，所有NFP计算时间为1/66×(10×2)2=6.08 s.但如果 RN=32，则计算时间将高达1/66×(10×32)2=1551.52s.

Burke等［8］在母材上布置一排垂线，零件沿线移动寻找最优旋转角使零件“包围盒”宽度最小.Dowsland等［9］指出:如将零件看作砂砾，母材看作玻璃瓶，不断摇晃“玻璃瓶”可使“砂砾”排列更紧密.这说明重力在排样中起到了重要作用.Lee等［10］在母材上布置多个排样点，在各点对零件进行旋转以找到最优排样姿态使零件形心坐标x，y最小.该算法本质上还是BL.

受Burke、Dowsland和Lee的启发，运用最小势能原理对排样问题的物理意义进行了解释，提出了不规则零件排样新算法HAPE，该算法不需要计算NFP.

1 排样问题的最小势能原理

结构力学最小势能原理:结构体系在受力和变形过程中总是尽量使总势能取得更小的值.

结构体系总势能Π表达形式如下

式中:Π为结构体系总势能;U为结构体系变形势能;V为结构体系位置势能.

排样问题中零件没有弹性变形(U=0).另外V=Gyc(G、yc分别为零件重力和形心高度).故

下面给出排样问题最小势能原理:零件在排样过程中总是尽可能地通过平移或旋转使其形心高度降低.

如图1所示，假设零件由多边形表达，含n个顶点和 n 条边(lq，q=1，2，…，n)，其面积和形心坐标可由格林公式导得:

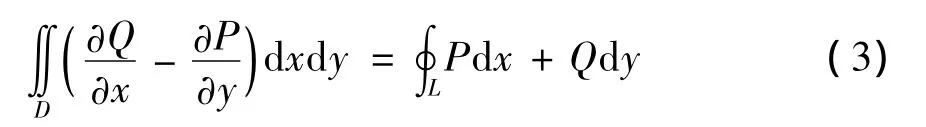
令式(3)中的P=－y，Q=0，则零件面积为

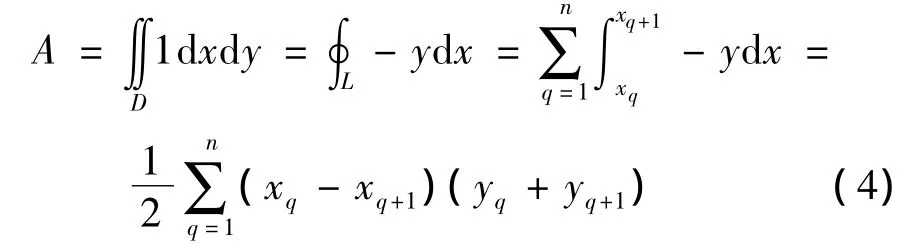
式中:xq、yq为顶点q的坐标;当q=n时，q+1=1.

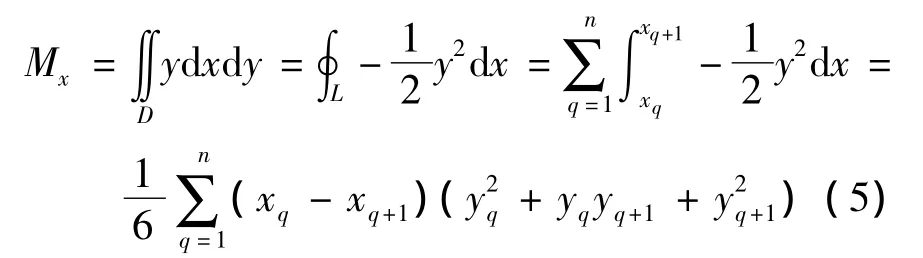
由式(4)、(5)可得到零件形心高度坐标 yc，yc=Mx/A.

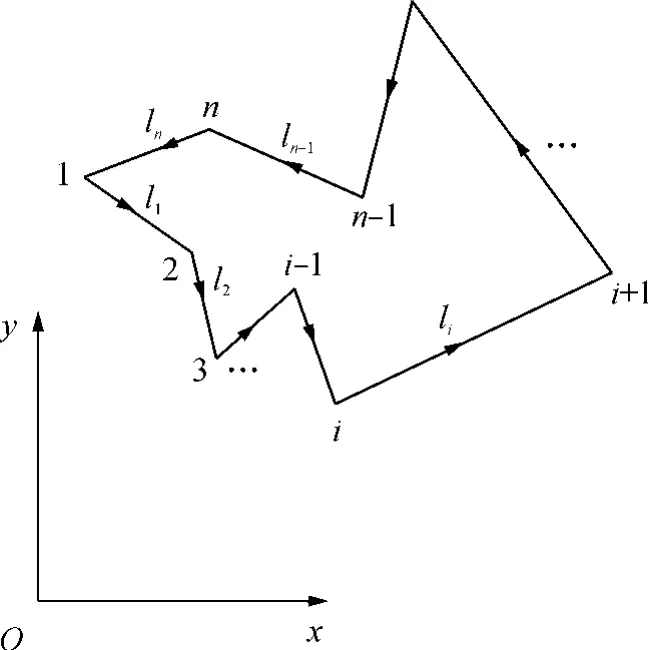
图1 多边形Fig.1 A polygon

如图2所示，某零件在不同的姿态下的形心高度是不同的.姿态2对应的形心最高，也最不稳定，零件在这种姿态下极易翻转;姿态4对应的形心高度最低，零件在这种姿态下是最稳定的.

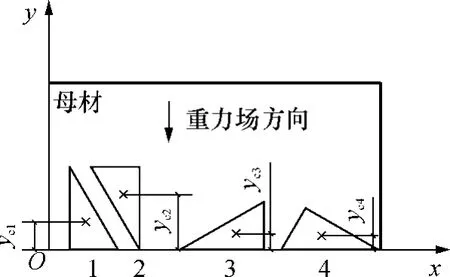
图2 不同姿态下的形心高度Fig.2 Different height of center with different attitude yc1－yc4为零件在不同姿态1－4下的形心高度

如图3(a)所示，4个矩形零件以“倒金字塔”方式置于母材底部.该排样姿态很不稳定，如受外界干扰，“倒金字塔”极易“倾覆”，如图3(b)所示.各零件将散落在母材底部，如受到图3(c)所示更“强烈”的外界干扰，零件将排列得更加紧密.

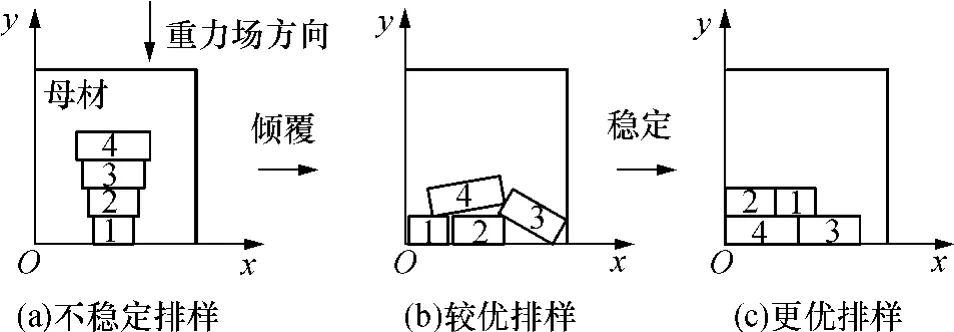
图3 倒金字塔零件的排样Fig.3 Layout of upside-down pyramid composed of shapes

2 定义

定义1 零件参考点(RP).

RP可以在任意位置选取.如图4所示，零件的平移和旋转均基于RP.

定义2 零件排样姿态(Att).

如图4所示，Att包含两个要素:RP和旋转角α.

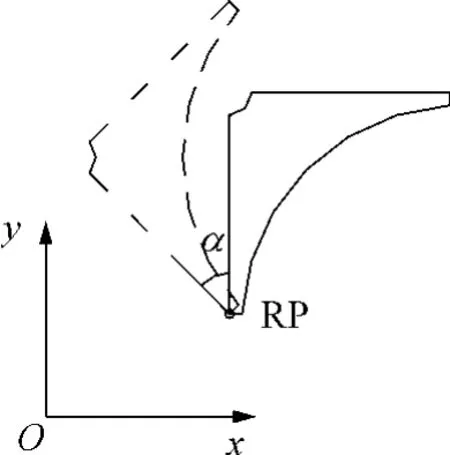
图4 参考点和排样姿态Fig.4 Reference point and nesting attitude

使用C语言定义Att:

定义3 排样点和排样点间距(PPD).

如图5所示，在母材上以一定的水平和垂直间距(PPD)布置的离散点被称为排样点.

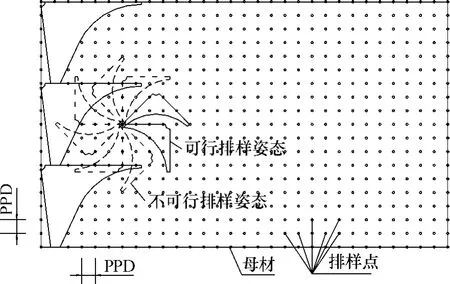
图5 排样点和排样姿态Fig.5 Nesting point and nesting attitude

定义4 可行排样姿态.

假设零件平移至某个排样点(参考点和排样点重合)，然后旋转某一个角度.如在此排样姿态下，该零件在母材内部且与其它零件不重叠，则称其为“可行”排样姿态.

如图4所示，零件旋转角定义如下:

式中:j=0，1，…，RN －1.

在每个排样点，零件有RN个排样姿态.如图5所示，虚线排样姿态为“不可行”排样姿态;实线的则为“可行”排样姿态.

3 基于最小势能原理的排样算法HAPE

HAPE的算法流程如图6所示.

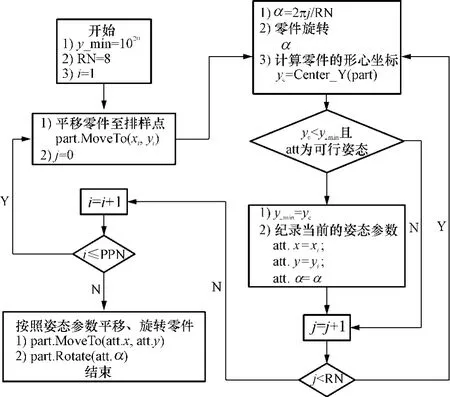
图6 HAPE流程图Fig.6 Flow chart of HAPE

流程图中有几个地方需要注意:

(a)PPN为排样点个数，xi，yi为第i个排样点的坐标(i=1，2，…，PPN);

(b)算法流程图中的零件旋转，实际上是将图1中的多边形顶点基于参考点进行旋转:

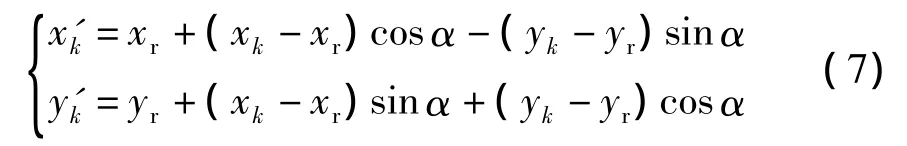
式中:xk，yk为零件顶点 k的坐标(k=1，2，…，n，n为零件顶点个数);xr，yr为零件参考点坐标;

(c)Center_Y(part)表示计算零件part形心坐标yc的函数，计算参考式(4)、(5).

4 算例

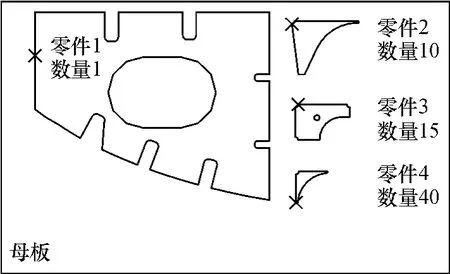
图7 母板和零件Fig.7 Stock sheet and part

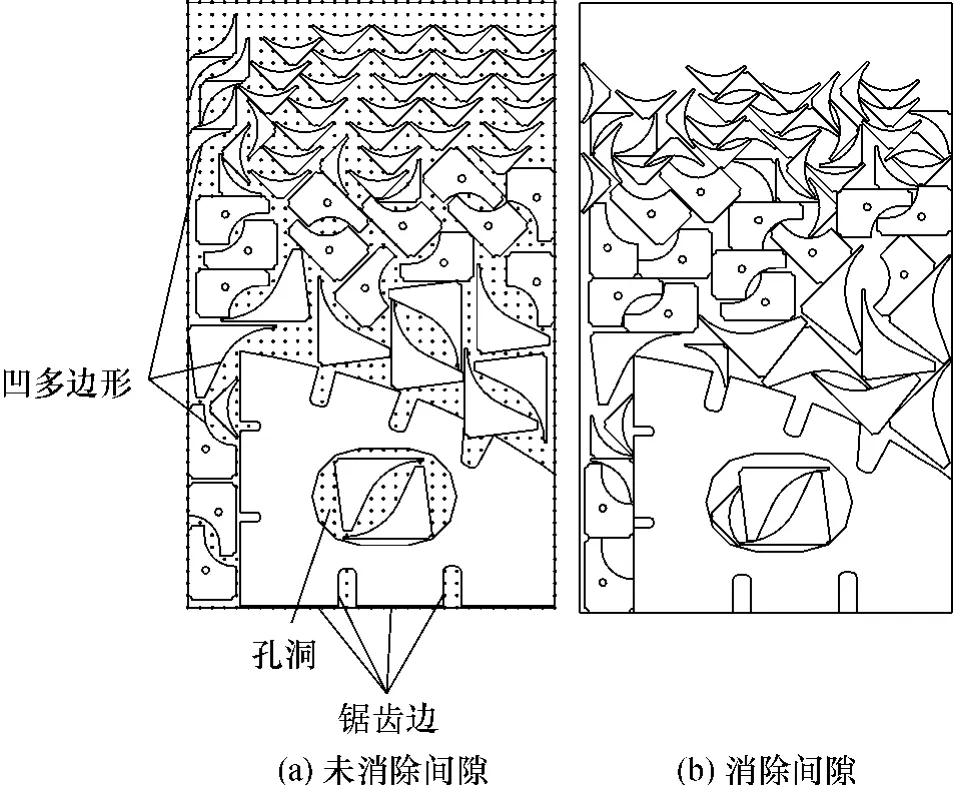
图8 HAPE排样图Fig.8 Layout by HAPE

对4种不同形状的船体零件(N=66)进行排样(图7中交叉点为参考点)，母材尺寸:5 000 mm×3050mm，PPD=100 mm，RN=8.零件1－4按照面积大小依次进行排样.在Visual C++6.0环境下编程，电脑处理器为2.66 GHz Celeron® CPU.如图8(a)所示，HAPE可以处理凹多边形零件以及具有锯齿边缘的零件，并可以利用孔洞进行排样.由于排样点是离散的，母材上仍然留下了很多的缝隙，缝隙大小与PPD成正比.如图8(b)所示，这种“天然”的缝隙可通过靠接算法消除之［11-12］，具体算法见参考文献［12］.如图9(a)所示，零件1、2之间以及零件1与母材底部之间存在空隙.如图9(b)所示，零件1通过垂向靠接消除了与母材底部之间的空隙;如图9(c)所示，零件2通过水平靠接消除了与零件1之间的空隙.

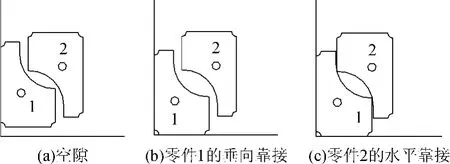
图9 通过垂向和水平移动消除空隙Fig.9 Elimination of gaps by vertical/horizontal moving

如果将PPD减至25 mm，排样效果如图10所示.使用软件Nestlib排样效果如图11所示.可以发现HAPE已经接近商业排样软件水平.

图10 HAPE排样图Fig.10 Layout by HAPE

图11 Nestlib排样图Fig.11 Layout by Nestlib

5 结论

综上所述，HAPE具有如下特点:(1)物理意义明确，算法简便，排样效果接近商业软件水平;(2)不需要计算NFP;(3)可以处理不规则零件，并利用孔洞进行排样;(4)HAPE的计算时间与排样点密度(1/PPD2)成正比，在计算速度上虽然与商业软件存在较大差距，但绝对的计算时间尚在可接受范围内.

需要特别指出的是:除了不需要计算 NFP，HAPE也不需要考虑“尽量向左”的准则.这两点正是HAPE与普通BL算法的最大区别.

［1］Baker B S，Coffman J E G，Rivest R L.Orthogonal packings in two dimensions［J］.SIAM Journal on Computing，1980，9(4):846-855.

［2］Liu De-quan，Teng Hong-fei.An improved BL-algorithm for genetic algorithm of the orthogonal packing of rectangles［J］.European Journal of Operational Research，1999，112(2):413-420.

［3］Chazelle B.The bottom-left bin-packing heuristic:an efficient implementation ［J］.IEEE Transactions on Computers，1983，C32(8):697-707.

［4］Art R C.An approach to the two-dimensional irregular cutting stock problem ［R］.Cambridge:IBM Cambridge Centre，1966.

［5］Dowsland K A，Vaid S，Dowsland W B.An algorithm for polygon placement using a bottom-left strategy［J］.European Journal of Operational Research，2002，141(2):371-381.

［6］Bennell J A，Dowsland K A，Dowsland W B.The irregular cutting-stock problem—a new procedure for deriving the no-fit polygon［J］.Computers ＆ Operations Research，2001，28(3):271-287.

［7］Burke E K，Hellier R S R，Kendall G，et al.Complete and robust no-fit polygon generation for the irregular stock cutting problem ［J］.European Journal of Operational Research，2007，179(1):27-49.

［8］Burke Edmund，Robert Hellier，Graham Kendall，et al.A new bottom-left-fill heuristic algorithm for the two-dimensional irregular packing problem ［J］.Operations Research，2006，54(3):587-601.

［9］Dowsland K A，Dowsland W B，Bennell J A.Jostling for position:local improvement for irregular cutting patterns［J］.The Journal of the Operational Research Society，1998，49(6):647-658.

［10］Lee Wenchen，Ma Heng，Cheng Borwen.A heuristic for nesting problems of irregular shapes［J］.Computer-Aided Design，2008，40(5):625-633.

［11］宋亚男，叶家玮，邓飞其，等.不规则图形排样系统中靠接算法比较研究［J］.计算机工程，2004，30(19):8-10.Song Ya-nan，Ye Jia-wei，Deng Fei-qi，et al.Analysis and comparison of collision algorithm in packing(nesting)［J］.Computer Engineering，2004，30(19):8-10.

［12］刘虓，叶家玮.基于多边形重叠检测的冲裁件优化排样［J］.锻压技术，2010，35(5):155-158.Liu Xiao，Ye Jia-wei.Optimal stamping blank layout based on algorithm of polygon intersection detecting［J］.Forging ＆ Stamping Technology，2010，35(5):155-158.