三边圆弧形横截面空心零件旋压成形应变网格实验*

赖周艺 夏琴香† 徐腾 程秀全

(1.华南理工大学机械与汽车工程学院，广东广州510640;2.广州民航职业技术学院机务工程系，广东广州510403)

非圆横截面空心零件旋压成形是国际上新兴的一种塑性成形工艺［1-2］.目前国内外的研究主要集中在该工艺的可行性和工装设计方面［3-6］.对于非圆横截面空心旋压件应力应变分布规律等成形机理的研究才刚刚起步.Hartal、夏琴香等［7-9］对某具体非圆横截面空心旋压件应力应变分布进行了数值模拟研究，尚缺实验验证.Shimizu［10］通过在坯料局部位置制备网格，初步研究了非圆横截面空心旋压件某些特殊位置的应变分布，欠全面和深入.文中以三边圆弧形横截面空心零件为研究对象，采用基于靠模驱动的非圆旋压成形装置进行应变网格实验，借助三维超景深显微镜和Mat LAB软件进行结果处理，研究了制件三向(母线方向、周向与厚向)应变分布规律和等效应变分布规律，深入探讨了影响应变分布的主要因素.

1 实验设计

三边圆弧形横截面空心零件如图1所示，由6个大小圆锥面组成，其横截面为6段相切的大小圆弧;相关尺寸参数如表1所示.材料为冷轧碳素钢薄板(SPCC).

实验采用圆形网格(记网格圆直径为d0，d0=5mm)，采用金属丝印油墨在毛坯板料上印刷应变网格(见图2).实验在自主研发的基于靠模驱动的非圆旋压成形装置(见图3)上进行［3］:坯料由尾顶夹紧在芯模上随着主轴一起旋转;芯模与靠模通过齿轮传动实现同步同角速度旋转;工作台A在伺服电机的驱动下沿机床的轴向(Z轴)作直线插补运动，实现旋轮轴向进给;安装在工作台B上的旋轮座(连同旋轮)在靠模的驱动下沿导轨作高速往复直线运动，实现旋轮径向往复进给;旋轮与芯模之间的间隙在成形过程中保持为坯料厚度(2 mm).坯料放置时将印有网格的表面放置在芯模一侧，以防止旋压过程中旋轮把网格磨掉.采用标准旋轮，旋轮直径为240 mm，圆角半径为7 mm.芯模转速n为45r/min，旋轮轴向进给比fz为0.15mm/r.

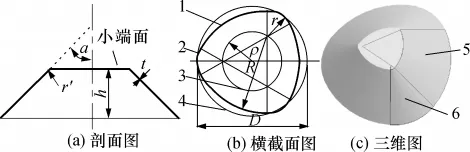
图1 三边圆弧形横截面空心零件示意图Fig.1 Schematic drawing of the hollow part with triangle arctype cross-section

表1 三边圆弧形横截面空心零件尺寸Table 1 Dimension of the hollow part with triangle arc-type cross-section

图2 坯料(含网格)Fig.2 Blank with grid

图3 基于靠模驱动的非圆旋压成形装置Fig.3 Non-circular spin-forming device based on profiling driving

2 实验结果

三边圆弧形横截面空心零件旋压成形过程如图4所示.

图4 空心零件的成形过程Fig.4 Forming process of hollow part

随着旋轮的进给，坯料在旋轮作用下逐点连续发生塑性变形;成形高度H＜31 mm(法兰宽度W＞24mm)时，坯料外轮廓保持不变，法兰区域保持直立和平整;成形高度H=31mm(W=24mm)时，坯料法兰区域开始出现起皱;随着旋压的继续进行，坯料外轮廓逐渐减少，法兰区域起皱的皱波逐渐增大;由于起皱不明显，其皱波在旋压过程中被旋轮压平.

旋压成形结束后应变网格如图5所示.为了便于讨论，将旋压件分为底部区域、圆角区、侧壁和口部(见图5).由于三边圆弧形横截面空心零件几何形状呈120°循环对称，应变分布亦为120°循环对称分布［8］.文中选取了图5所示剖面线区域(大于120°对应区域)进行测量和分析，可全面反映三边圆弧形横截面空心零件应变分布规律.由图5可见，底部区域网格保持不变，侧壁网格沿母线方向发生明显的拉长而形成椭圆.文中主要对侧壁和口部的应变进行测量和分析.网格变形后形成的椭圆之长、短轴分别记为d1和d2，其分别与母线方向和周向对应.根据长、短轴的长度和网格原始直径d0可求得母线方向和周向的应变εz和εθ:

根据体积不变原理可得厚向应变εt:

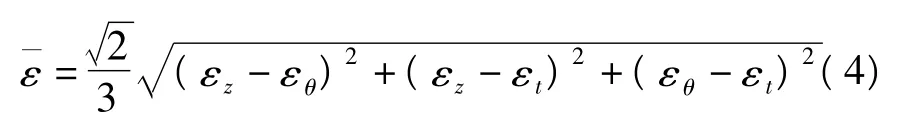
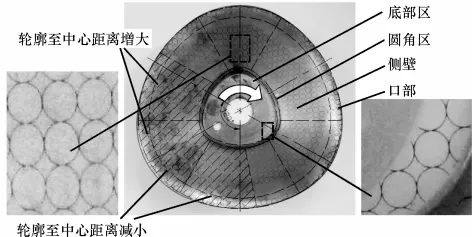
图5 旋压成形件Fig.5 Spun part

采用超景深三维显微镜VHX-600E放大20倍对网格圆进行逐个测量，通过Microsoft Office Excel 2003软件计算得到εz、εθ、εt和.借助Mat LAB 7.0软件绘制得到上述应变的等值线图，见图6.

3 实验结果分析

3.1 变形方式与应变状态

平板坯料拉深旋压某种程度上包含有剪切旋压的成分;在法兰宽度不小于某一临界值前平板坯料拉深旋压实际上为剪切旋压，在法兰宽度小于临界值后则是同时兼有剪切旋压和拉深旋压的复合变形［11-12］.由图4可见三边圆弧形横截面空心零件旋压成形底部圆角区和侧壁时，坯料外轮廓保持不变，符合剪切旋压的特征;由图6可见侧壁的应变属于一向拉伸、两向压缩的应变类型(应变状态图见图7)，母线方向受拉伸、周向和厚向受压缩，其中εθ远小于εz和εt;由此可知旋压成形侧壁时坯料变形方式为剪切旋压［11］.旋压成形口部时，坯料外轮廓逐渐减小;口部应变同样属于母线方向受拉伸、周向和厚向受压缩的一向拉伸、两向压缩的应变类型，其中εθ较小，以εz和εt为主;与侧壁周向应变εθ相比，口部的周向应变εθ有所增大.由此可知旋压成形口部时坯料变形方式是以剪切旋压为主、兼有拉深旋压的复合变形.

3.2 应变分布

母线方向应变εz分布:该方向应变的范围为［0.06，0.34］，从圆角区至口部，应变值先增大然后减小.记大圆锥面侧壁中下部中间部位为A区，大小圆锥面侧壁中部连接部位为B区，小圆锥面侧壁中部中间部位为C区(见图6(a)).母线方向应变最大值(0.34)出现在A、B和C区域，且A区面积比C区大.应变最小值出现在口部.大小圆锥面中间母线两侧的应变不完全对称，横截面轮廓至中心距离增大一侧(具体位置见图5)的应变比距离减小一侧大.

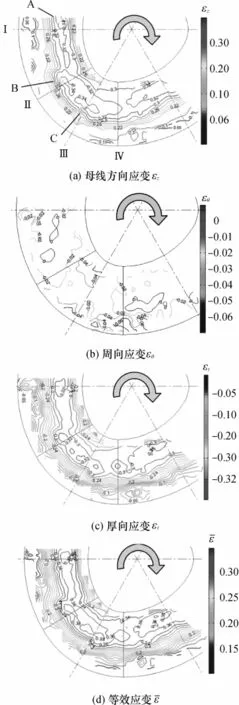
图6 应变等值线图Fig.6 Strain contour maps

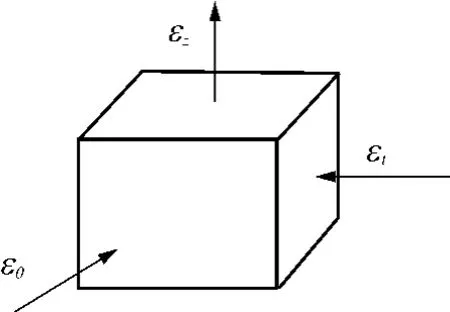
图7 旋压件侧壁和口部的应变状态图Fig.7 Strain status in side wall and opening area of spun part

周向应变 εθ分布:该方向应变的范围为［- 0. 06，0］，应变值总体较小( 其最大应变值比εz和εt小一个数量级).最大应变出现在大小圆锥面口部.侧壁应变范围为［-0.04，0］，最小应变值(0)出现在大圆锥面中部中间位置.

厚向应变εt分布:该方向应变的范围为［-0.32，-0.05］，其变化趋势与母线方向应变εz一致.

侧壁母线Ⅰ、Ⅱ、Ⅲ和Ⅳ(见图6(a))上应变的分布如图8所示.由图8可明显看出各母线上的应变主要为母线方向应变εz和厚向应变εt，且随高度的变化而发生明显变化;周向应变εθ最小且变化较小.各母线上母线方向应变εz、厚向应变εt和等效应变在侧壁中部附近同时出现绝对值最大值，但不同母线上最大值对应的高度不同.母线Ⅰ、Ⅱ、Ⅲ和Ⅳ上最大值对应高度分别为18.0、22.5、27.5和24.5mm.比较母线Ⅰ(大圆锥面中间母线)和Ⅲ(小圆锥面中间母线)的应变分布可明显看出，小圆锥中间母线上不仅变形较大，而且高度7 mm至42 mm均为变形较大区域.母线Ⅱ与Ⅳ均为大小圆锥面的连接线，但应变变化不同，前者较接近于母线Ⅰ，而后者较接近于母线Ⅲ.

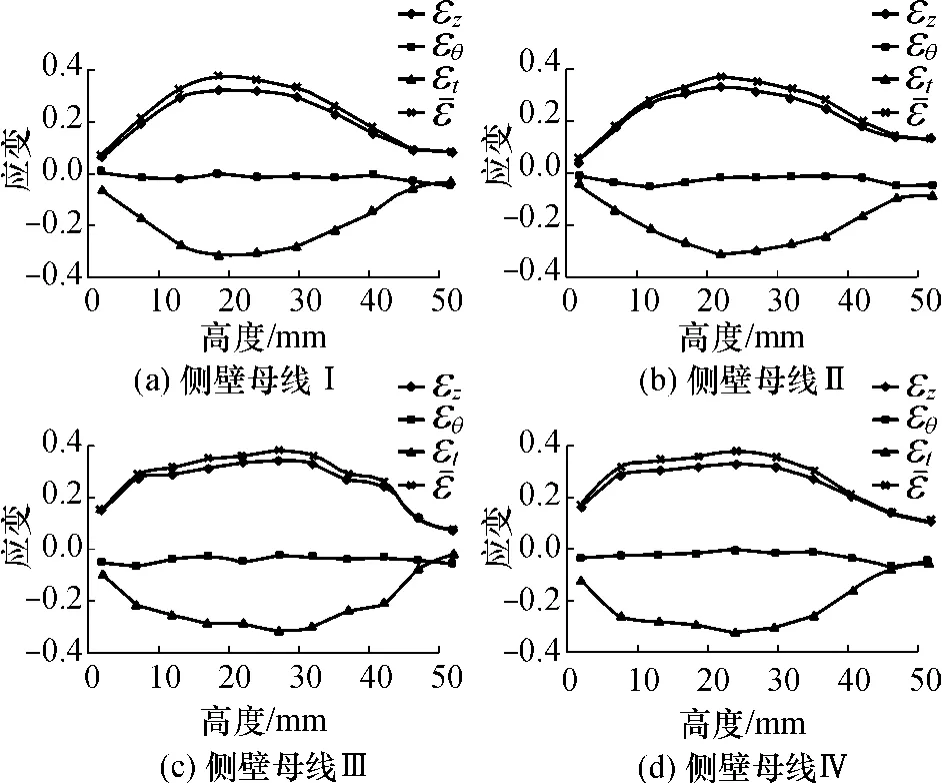
图8 应变沿侧壁母线分布Fig.8 Distribution of strain along side wall generatrix

3.3 应变分布影响因素

三边圆弧形横截面旋压件应变分布主要受变形程度和变形速度的影响.

(1)变形程度.

一般采用相对高度h/d2(高度/大端直径)、相对锥顶直径d1/d2(大端直径/小端直径)和半锥角α等来衡量锥形件的变形程度(见图9)［13］.文中采用相对高度h/d2来衡量三边圆弧形横截面旋压件不同部位的变形程度.大圆锥面相对高度h/d2≈0.16，属于浅锥形件(0.10＜h/d2＜0.25)，成形过程中坯料的变形程度较小;小圆锥面相对高度h/d2≈0.34，属于中锥形件(0.30＜h/d2＜0.70)，成形过程中坯料的变形程度较大.因此小圆锥面与大圆锥面之间应变分布不相同，小圆锥面侧壁较大应变的区域比大圆锥面侧壁大.

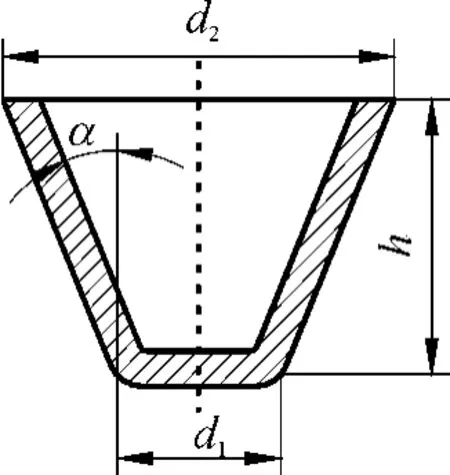
图9 锥形件示意图Fig.9 Schematic drawing of the conical part

(2)变形速度.

旋压变形速度可用旋轮轴向进给比来衡量.由于成形过程旋转中心不在组成三边圆弧形横截面空心零件的大小圆锥面的中心，其横截面轮廓上不同点到旋转中心的距离是变化的，这就导致成形过程中旋轮与坯料的接触点不稳定，在旋轮中心线与旋转中心线所在平面上下移动.图10所示为旋轮无轴向进给、芯模旋转一周时旋轮接触点的轨迹，图中标示的圆点为旋轮接触点在芯模每转过10°时的实际位置;通过测量可知在大圆弧(对应大圆锥面)中点附近，芯模转动10°时旋轮接触点转过的角度为14.5°，达到了芯模转动角速度的1.45倍;而在小圆弧(对应小圆锥面)中点附近，芯模转动10°时旋轮接触点转过的角度仅为5.6°，仅为芯模转动角速度的0.56倍.旋轮接触点位置的变化导致接触点转动角速度的变化;接触点转动角速度的变化又将导致接触点瞬时轴向进给速度的变化.由于旋轮轴向进给速度保持不变(轴向进给速度vf=fzn/60=2πfcω，ω为芯模转动角速度)，接触点角速度的增大意味着旋轮接触点轴向瞬时进给比(简称旋轮瞬时进给比，记为f'z，f'z=vf/(2π ω')，ω'为接触点角速度)降低;以图10所示位置为初始位置，芯模转动一周时旋轮瞬时进给比f'z与旋轮轴向进给比fz之比(f'z/fz)如图11所示.

由小圆弧(对应小圆锥面Ⅱ)中点到两侧，f'z/fz首先由1.764缓慢增加至1.767然后迅速降低(在与大圆弧连接时降低至1.351);f'z的变化导致同一横截面上小圆锥面母线方向应变和厚向应变从中心，而导致小圆锥面同一横截面上应变的不相等.

而对于大圆弧(对应大圆锥面)，由其中点到两侧，f'z/fz首先缓慢增大然后迅速增大(在与小圆弧区连接处最大，f'z/fz=1.351)，变化幅度较大，但由于该圆锥面变形程度相对较小，所以其同一横截面应变不相等的现象不显著.

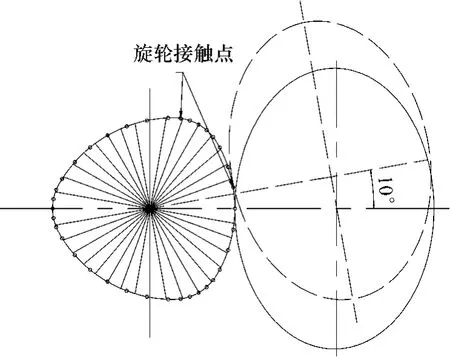
图10 旋轮接触点的变化Fig.10 Variation of contact point between roller and blank

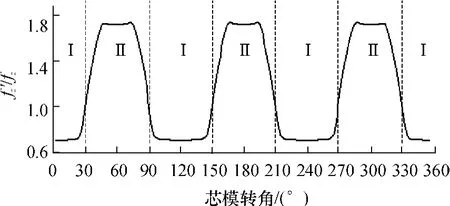
图11 旋轮瞬时进给比的变化Fig.11 Variation of roller feed ratio along axial direction

此外，靠模驱动非圆旋压成形装置旋轮的径向运动也对应变分布有一定影响.制件横截面轮廓至旋转中心的距离逐渐减少时，靠模推动滚轮带动旋轮实现径向前进;而制件横截面轮廓至旋转中心的距离逐渐增大时，则是坯料推动旋轮实现径向后退，因而会产生附加压应变，使得大小圆锥面横截面轮廓至中心距离增大一侧的应变比减小一侧大.

4 结语

以三边圆弧形横截面空心零件为研究对象，进行了应变网格旋压成形实验研究，结论如下:

(1)旋压件侧壁和口部属于母线方向受拉、周向和厚向受压的应变状态，其中周向应变很小，以母线方向和厚向应变为主;侧壁成形时坯料变形方式是剪切旋压，口部成形时坯料变形方式是以剪切旋压为主、兼有拉深旋压的复合变形.

(2)大小圆锥侧壁母线方向应变、厚向应变和等效应变的变化规律一致.从圆角区至口部，应变先增大后减小，但小圆锥面侧壁产生较大应变的区域比大圆锥面大;从中心到两侧，大圆锥面的应变变化小，小圆锥面的应变变化明显.在同一圆锥面的侧壁上，横截面轮廓至中心距离增大一侧的应变比减小一侧大.

(3)应变分布主要受变形程度和变形速度影响.大小圆锥面变形程度的不同导致大小圆锥面侧壁同一横截面上应变分布不相同;横截面上不同位置接触点角速度的变化导致旋轮接触点轴向瞬时进给比不恒定，使得变形速度不恒定，导致大小圆锥面横截面上应变分布不一致.

(4)基于靠模驱动的旋压成形装置在旋轮径向后退时产生附加压应变，使得大小圆锥面横截面轮廓至中心距离增大一侧的应变和减小一侧不相同.

［1］Musica O，Allwooda J M，Kawai K.A review of the mechanics of metal spinning［J］.Journal of Materials Processing Technology，2010，210(1):3-23.

［2］Awiszus B，Meyer F.Metal spinning of non-circular hollow parts［C］∥Proceedings of the 8th International Conference on Technology of Plasticity.Verona:［s.n.］，2005:353-355.

［3］Xia Qin-xiang，Lai Zhou-yi，Zhan Xin-xi，et al.Research on spinning method of hollow part with triangle arc-type cross section based on profiling driving［J］.Steel Research International，2010，81(9):994-997.

［4］Arai H.Robotic metal spinning forming non-axisymmetric products using force control［C］∥Proceedings of the 2005 IEEE International Conference on Robotics and Automation.Barcelona:IEEE，2005:2691-2696.

［5］Arai H.Force-controlled metal spinning machine using linear motors［C］∥Proceedings of the 2006 IEEE International Conference on Robotics and Automation.Orlando:IEEE，2006:4031-4036.

［6］Sekiguchi A，Arai H.Synchronous die-less spinning of curved products［J］.Steel Research International，2010，81(9):1010-1013.

［7］Hartal S，Awiszus B.Numerical and experimental investigations of production of non-rotationally symmetric hollow parts using sheet mental spinning［J］.Steel Research International，2010，81(9):998-1001.

［8］夏琴香，吴小瑜，张帅斌，等.三边圆弧形横截面空心零件旋压成形的数值模拟及试验研究［J］.华南理工大学学报:自然科学版，2010，38(6):100-106.Xia Qin-xiang，Wu Xiao-yu，Zhang Shuai-bin，et al.Numerical simulation and experimental investigation of spinning of hollow part with triangular arc section［J］.Journal of South China University of Technology:Natural Science Edition，2010，38(6):100-106.

［9］吴小瑜.四边圆弧形横截面空心零件旋压成形数值模拟及实验研究［D］.广州:华南理工大学机械与汽车工程学院，2010.

［10］Shimizu I.Asymmetric forming of aluminum sheets by synchronous spinning［J］.Journal of Materials Proce-ssing Technology，2010，210(1):585-592.

［11］Quigley E，Monaghan J.Metal forming:an analysis of spinning process［J］.Journal of Materials Processing Technology，2000，103(1):114-119.

［12］Kang Da-chang，Gao Xi-cheng，Meng Xiao-feng，et al.Study on deformation mode of conventional spinning of plates［J］.Journal of Materials Processing Technology，1999，91(3):226-230.

［13］李健.圆锥形零件极限拉深系数及合理压边力的研究［D］.重庆:重庆大学机械工程学院，2002.