区域公交车辆调度及购车计划的双层规划模型*

魏明 靳文舟 孙博

(华南理工大学土木与交通学院，广东广州510640)

区域公交车辆调度(RBSP)是当今城市公共交通发展趋势之一，根据某区域内多条线路(上下行)在不同时段发车频率的不均衡，考虑多车型［1-2］、站场容量、燃料等约束因素［1-8］，通过车场内或插入空驶班次实现车辆跨线调度可以有效提高车辆利用效率和降低营运成本.Bertossi等［9］已证明 RBSP为NP-hard问题，关于RBSP的相关文献分类为静态RBSP和动态RBSP［1-10］，可归结为基于“班次节点”的最大网络流问题和“被某车辆完成的所有班次”的集合划分问题的混合整数规划模型［1-10］.与前者比较，后者研究相对简单的多，但相关研究文献却很少.

购车计划是确定车辆调度方案的每辆车最佳车型使购车成本最少，考虑不同车型污染气体排放量等因素.目前，国内外学者鲜有探讨公交车辆调度和车辆采购计划之间的有机联系，仅文献［8］中探讨了在购车预算和污染物排放量限制等约束条件下如何制定车辆调度方案使营运费用最小的问题，但不能保证从系统的角度是最优的.

从系统最优角度，文中首次建立区域公交车辆调度和购车计划之间的双层规划模型，探讨它们之间的有机联系，在上层规划中，考虑污染气体排放量等因素，确定车辆调度方案的所有车辆的最佳车型使购车费用最少;在下层规划中，合理派车完成所有固定时刻表的公交班次，在满足车场容量、燃料及车辆完成任务返回车场最迟时间等约束因素情形下，制定一个最优的车辆调度方案使车辆利用率最大.根据问题特征，该问题可等价转化为不同车辆数情形下的最佳车辆调度方案及相应采购策略问题，设计求解相应问题的遗传算法染色体编码、初始种群产生及遗传操作机制等，通过一个简单算例给出最佳车辆调度方案及相应车辆采购计划.

1 区域公交车辆调度及购车计划的双层规划问题

1.1 购车计划的上层规划问题

在车辆调度方案可知的情形下，上层规划U把U看作指派问题［11］，考虑每辆车仅对应一类车型、每车型至少有一辆车及某污染气体排放量限制等约束因素，以如何制定购车策略使购车费用极小化为目标，建立一类0-1整数规划模型如下所示.

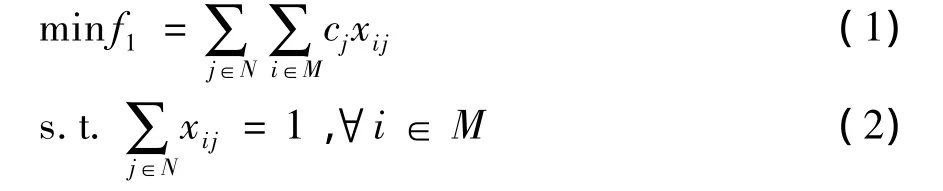
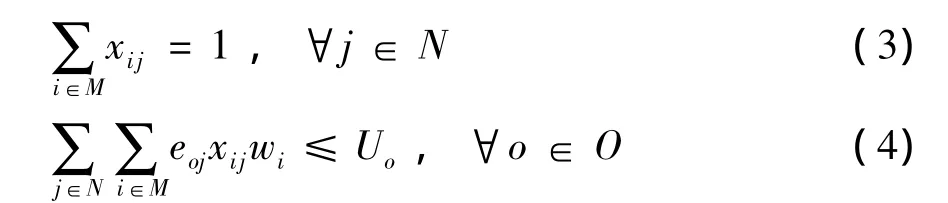
式中:M为车辆集合;N为车型集合;O为污染气体集合;wi为车辆i的实际工作时间;cj为车型j的车辆价格;Uo为某污染气体o∈O的排放量上限;eoj为第j类型车辆在每小时排放某污染气体o∈O的量;xij表示车辆i是否为车型j.

在上述上层规划U模型中，式(1)是问题的目标函数，表示购买公交车辆的费用最少;式(2)－(4)是约束条件，其中式(2)表示每辆车仅对应一类车型，式(3)表示每车型至少有一辆车，式(4)表示所有公交车的某污染气体排放量不超过上限.

1.2 区域公交车辆调度的下层规划问题

假设不同公交线路的公交车辆可以为任意车型，下层规划L把RBSP看作“被某车辆完成的所有班次”的集合划分问题［11］，考虑车场容量、燃料和最迟返回车场时间等约束因素，以车辆数、车辆等待和空驶时间最少为目标建立一类混合整数规划模型，如下所示.

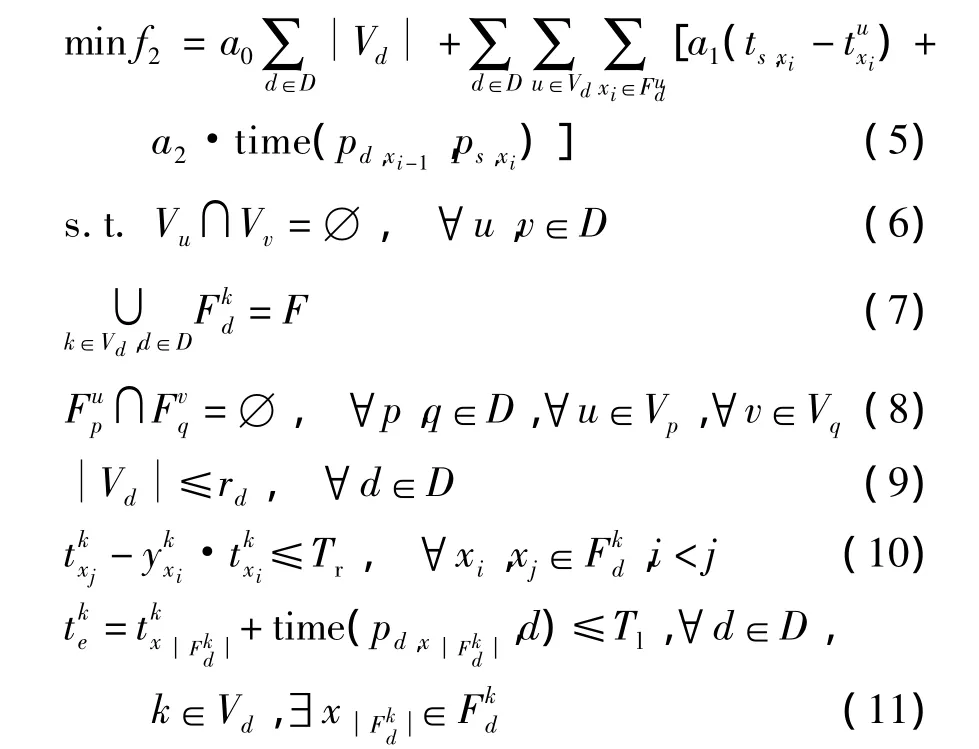
式中:F为所有线路的固定时刻表对应班次集合，F={F1，F2，…，F|F|}对任意班次∀Fi∈F，要求车辆在开始时刻 ts，Fi从起始车场 ps，Fi出发和在结束时刻te，Fi到达终点车场 pd，Fi;D 是车场集合，Vd和 rd分别为从车场∀d∈D出发的车辆集合及相应车场容量;任意车辆∀k∈Vd在时刻离开车场d完成一系列班次在时刻途 经 某 班 次的出发点 ps，xi，若在该车场花费补充燃料时间为Tf(取最大值)，则=1和表示车辆k在某班次的出发车场ps，xi花费时间补充燃料;显然，车辆∀k∈Vd依次执行班次xi－1和满足 te，xi－1+time(pd，xi－1，ps，xi)≤ts，xi，若 time(pd，xi－1，ps，xi)≠0，这种车场借用情形下的空车行驶称为空驶班次(DH)，其中time(u，v)表示车辆在两车场u和v的空驶时间;Tl表示车辆最迟返回所属车场的时间;表示集合X的元素数量;Tr为不同类型车辆的最大行驶时间，取最小值.

在上述下层规划L模型中，式(5)为问题的目标函数，追求车辆利用效率极大化，即车辆数a0、车辆等待a1和空驶时间a2最少;式(6)－(11)为约束条件，其中式(6)表示某车辆仅属于一个车场，式(7)确保所有的公交班次都被车辆执行，式(8)表示一辆车同时只能执行一个公交班次及一个公交班次只能被一辆车执行，式(9)保证任意时刻车辆入车场满足其容量限制，式(10)表示车辆在执行某公交班次前是否补充燃料，式(11)保证每辆车在某时刻前返回所属车场.

2 求解上下层规划问题的遗传算法

双层规划的非凸性特点决定求解该问题是NPHard 难题［3，12-13］，求解的关键在于设计问题的反应函数具体形式，对连续变量可以利用灵敏度分析方法分析变量之间的导数关系简化反应函数，而关于离散变量却没有好方法.遗传算法(GA)是Holland于20世纪60年代提出的一种借鉴生物性法则“适者生存，优胜劣汰”演化而来的求解复杂问题的通用框架的随机化搜索方法，具有自组织、自适应和自学习性等特点［14］.

文中双层规划模型具有以下特点:

(1)L和U均为离散变量，计算时间复杂性与问题规模成指数关系;

(2)U的xij、M和wi与L的Vd和之间是有机联系，即受约束条件(4)限制的M直接和间接影响Vd和，当Vd和被确定后可计算和每辆车∀i∈M的工作时间 wi=time(d，x1)+由U确定xij.

针对模型特点，该问题可转为求解不同车辆数情形下的关于xij和的上下层规划问题，设计GA求解相应问题的编码方案、初始种群产生方法等，计算每种车辆数情形下相应问题的最佳车辆调度方案及购车计划，最后比较所有可行组合下的目标值确定最优解.

2.1 编码方案

上层规划的一个解用向量 XU=(x1，x2，…，x|M|)表示，每个元素xi取值为之间的整数，相关含义为:第i车的采购车型为xi.例如:某购车计划方案对应染色体编码X=［1 2 3 1 2］，蕴含信息为车1和4的车型为1，车2和5的车型为2，车3的车型为3，若方案满足式(4)约束，则X是一个不可行解.

下层规划的一个解用向量 XL=(x1，x2，…，x|F|)表示，每个元素 xi取值为之间的整数，相关含义为:车辆xi完成第i班次.例如:某车辆调度方案对应染色体编码X=［1 2 1 1 2 1 2 1］，蕴含信息为车辆1完成第1、3、4、6和8班次，车辆2完成第2、5和7班次，各班次在相应车辆的服务顺序由自身的发车时刻决定，若它们均满足下层规划的各种约束因素，则X对应一个可行解.

2.2 产生初始种群

对于上层规划，不遵守式(4)的随机产生的个体是一个不可行解，设计启发式算法生成可行个体，组成求解该问题的遗传算法初始种群.启发式算法的具体步骤如下.

(2)查找车辆∀i∈M的可行车型集合N'⊂N(令N'=∅，对∀o∈O，若∀u∈N且∃v∈N满足，则 N'=N'∪{u})，从 N'中随机选择某车型∀k∈N'，对应可行解向量XU的元素xi=k，令∀o∈O 的 Uo'=Uo'－eokwi及 M=M －{i}.

(3)若M≠∅，转至步骤(2);否则，算法终止并输出结果.

对于下层规划，RBSP涉及的众多因素是强约束，随机产生一个可行个体的概率很低，设计启发式算法求得不同可行个体，组成求解该问题的遗传算法初始种群.启发式算法的具体步骤如下.

(1)对班次集合 F 根据∀Fi∈F 的 ts，Fi进行升序排序，获取 F'={F'1，F'2，…，F'|F|}.

(3)查找可以完成F'i的车辆集合C(详细过程如操作－所示)，若C≠∅，从中随机选择车辆∀k∈C完成F'i，对应可行解向量XL的元素xT'i=k，转至步骤(4);否则，转至步骤(2).

(4)令 i=i+1，若 i≤F ，转至步骤(3);否则，算法终止输出结果.

2.3 适应度函数的设计

对上下层规划的种群根据个体目标函数值进行降序排序，每个个体排序位置s决定相应适应度值，构造它们相应的适应度函数如下［14］:

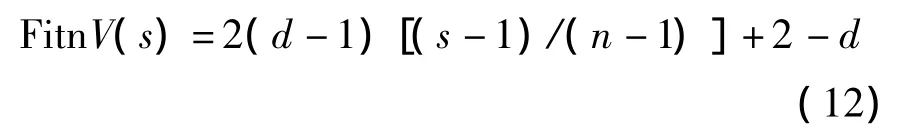
式中:n为种群大小;d表示选择的压差，默认值为2.

2.4 遗传操作

选择、交叉和变异是GA的三种基本运算［14］，文中对选择运算采用轮盘赌选择法和精英保留法组合的策略，从当前父代群体中选出优良的个体繁殖下一代;对交叉运算以一定概率根据单点交叉算子从一组父辈个体染色体对应基因段的交换产生一组新个体;对变异运算根据基本位变异算子对个体的每一个基因座依据变异概率判断是否为变异点，对变异点做相关运算产生出新个体，避免由于选择和交叉运算而造成的某些信息损失，从而维持群体多样性.

显然，对于上下层规划，交叉和变异算子产生的新个体也许不是可行解，这些个体被舍弃.

2.5 终止原则

终止原则为种群完成预先给定的进化代数，或者相邻若干代种群平均适应度(最优个体)未变化.

3 数值实验

某公司在同一区域内的3个车场经营5条线路(rd=15，d=1，2，3)，拟采购一定数量的 3 种车型公交车完成所有公交班次，使污染气体NOx、CO、HC及CO2的排放量限制在 0～195 kg、0～335 kg、0～35kg及0～4200kg.不同车型信息如表1所示，每条公交线路及固定时刻表如表2和3所示，各车场之间空驶时间如表4所示，相关参数Tr=480min、Tf=20min和 Tl=1290min.

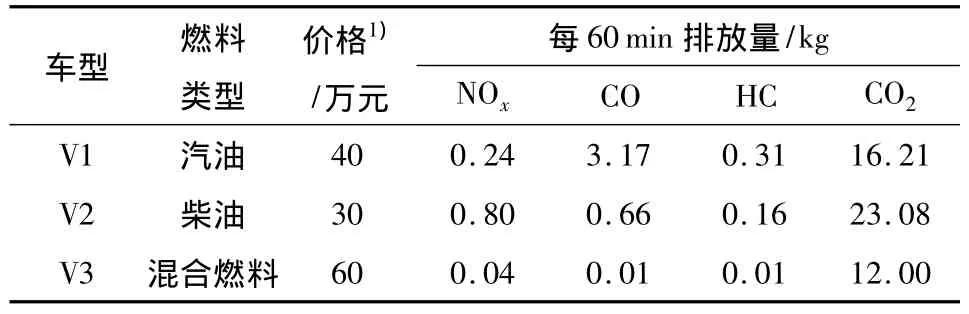
表1 公交车辆信息Table 1 Bus information

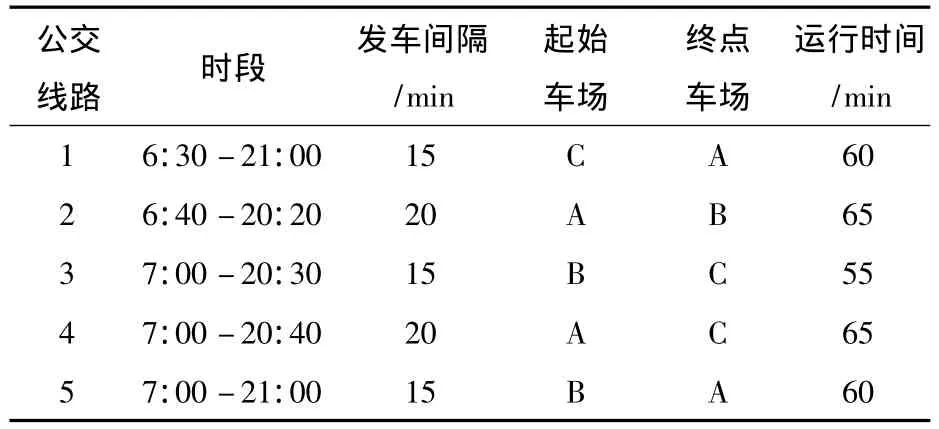
表2 公交线路信息Table 2 Route information of bus

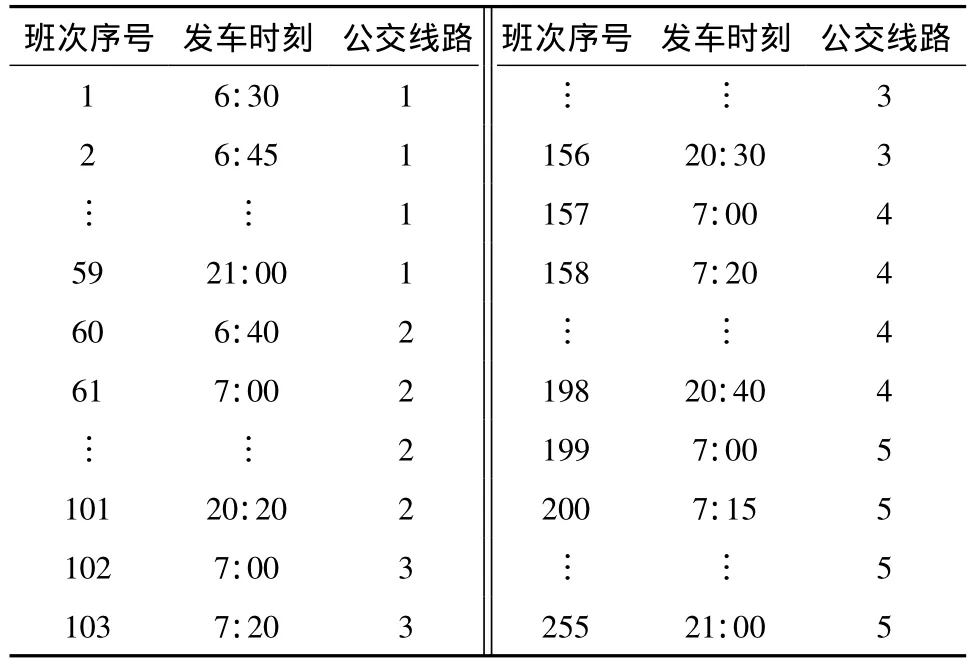
表3 行车时刻表Table 3 Timetable information

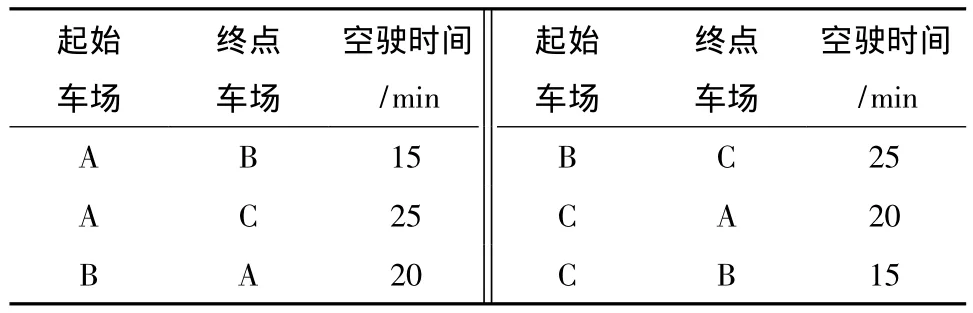
表4 空驶时间一览表Table 4 Deadhead time information

文中采用Sheffield的遗传算法Matlab工具箱函数编写求解上下层规划的程序，设置相关参数如下:最大迭代次数为10000，染色体数为100，交叉率为0.7，变异率为0.05，a0=1000，a1=1.5，a2=10，对车辆数为24(无解)、25、26、27、28 及29 每种情形下均运行50次，计算它们的上下层规划的最佳方案如表5和6所示，从中可知:随着车辆数增加，不同方案的所有车辆的总等待时间增多，空驶时间稍微减少使总行驶时间差别不大，因不同车型的各种污染气体排放量是不同的，所以需购买一定数量的V3才能满足各种污染气体最大排放量限制，导致购车费用逐渐变多.

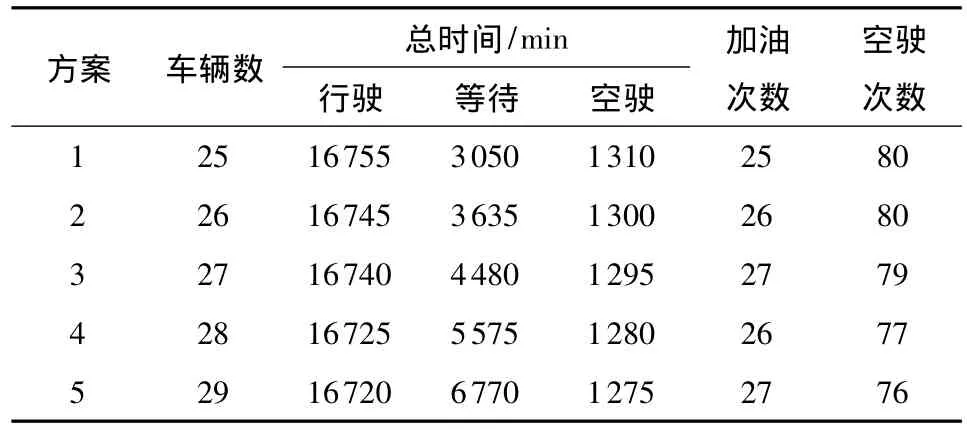
表5 不同车辆数下层规划的最佳方案Table 5 Optimal solution to lower level plan under different number of vehicles

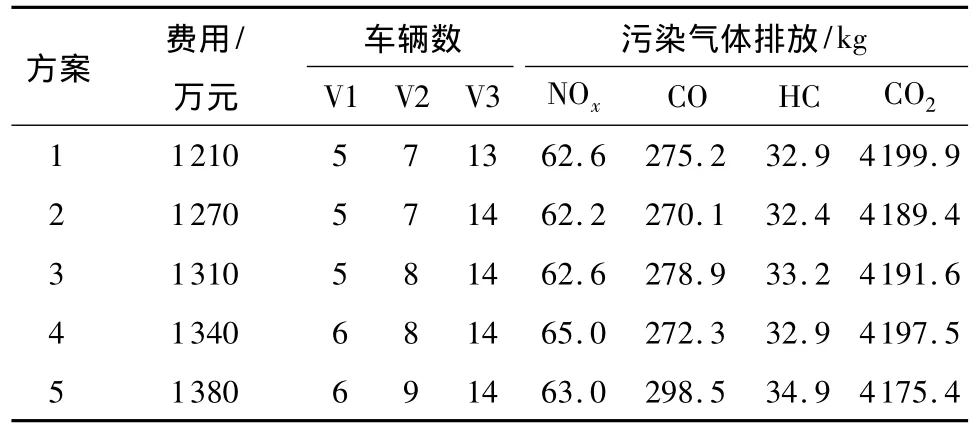
表6 不同车辆数上层规划的最佳方案Table 6 Optimal solution to upper level plan under different number of vehicles

方案1为模型最优解，对应车辆调度方案如表7所示，总共需派遣25辆车(从车场A、B和C初始出发的车辆数为7、10和8)，经加油25次(车场A加油12次、车场B加油5次和车场C加油8次)和空驶80次(A空驶至B为30次，A空驶至C为6次，B空驶至A为2次，C空驶至A为8次，C空驶至B为34次)，可以完成255个班次，所有车辆的总行驶、等待及空驶时间分别为16 755、3 050和1310min，不同污染气体 NOx、CO、HC 及 CO2的总排放量分别为 62.6、275.2、32.9 和 4199.9kg.

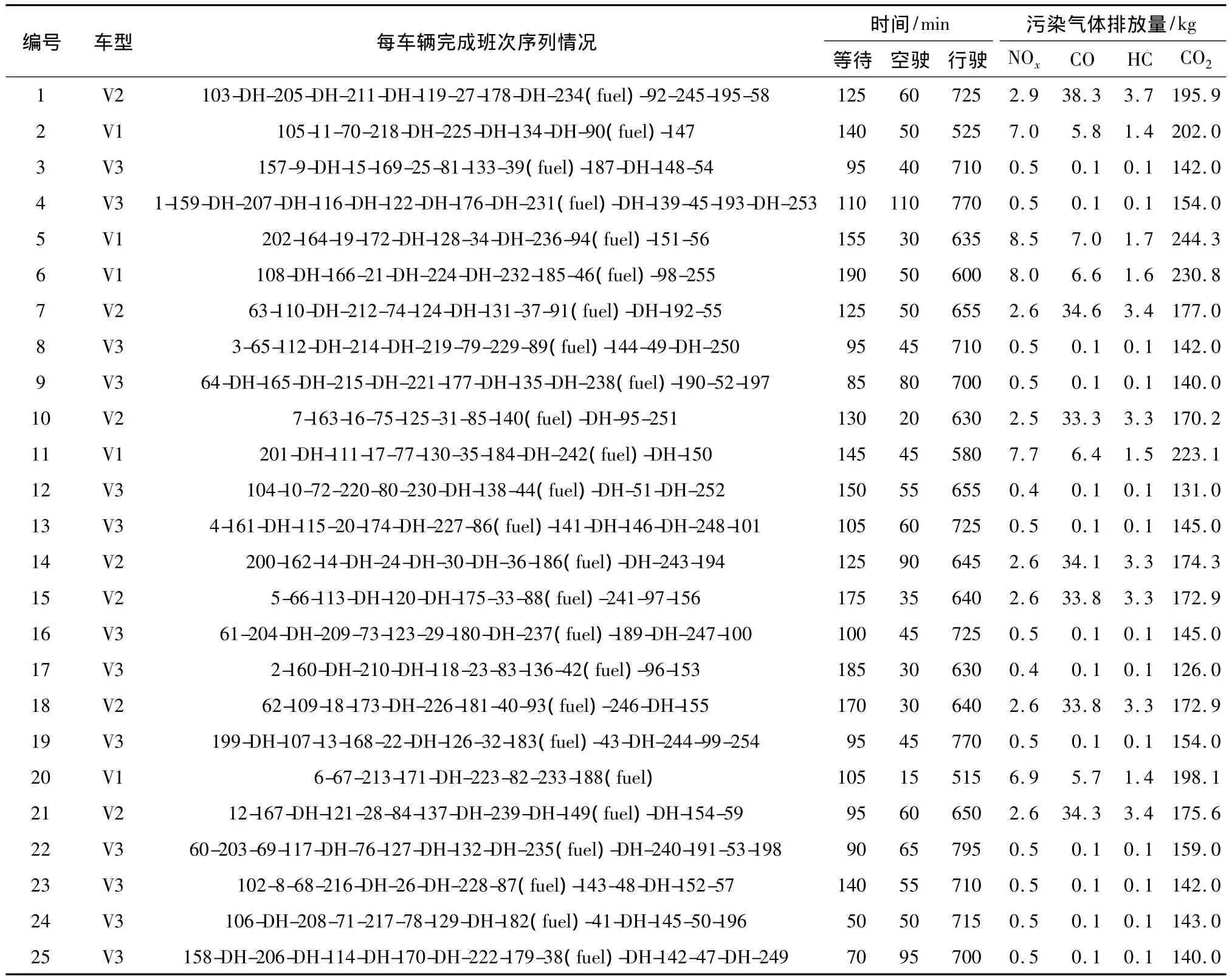
表7 最佳车辆调度方案Table 7 Best results of vehicle scheduling

4 结语

文中借助双层规划原理探讨了区域公交车辆调度和购车计划之间的有机联系，通过一个简单算例求解相应最佳车辆调度方案及购车策略满足车场容量、燃料限制及各种污染气体最大排放量等约束因素，证明了模型和算法的可行性.实验结果表明:在各种污染气体最大排放量“强”约束情况下，随着车辆数增加，不同方案的总行驶时间虽逐渐减少但相差不大，若利用很多“低档”车替换“高档”车，必然导致破坏某污染气体排放限制，所以需购买一定数量的“高档”车才能满足各种污染气体最大排放量限制，导致购车费用逐渐变多.

但是文中未考虑现实交通中的交通拥堵及其引起的交通事故等不确定事件，这些因素影响车辆未按时完成某班次从而可能导致车辆不能依原计划继续执行未完成的班次序列，出现了车辆调度方案可靠性问题.这将是今后进一步研究的方向.

［1］Natalia Kliewer，Taïeb Mellouli，Leena Suhl.A time-space network based exact optimization model for multi-depot bus scheduling［J］.European Journal of Operational Research，2006，175:1616-1627.

［2］Vitali Gintner，Natalia Kliewer，Leena Suhl.Solving large multiple-depot multiple-vehicle-type bus scheduling problems in practice［J］.OR Spectrum，2005，27:507-523.

［3］刘志刚，申金生.区域公交时刻表及车辆调度双层规划模型［J］.系统工程理论与实践，2007，27(11):135-141.Liu Zhi-gang，Shen Jin-sheng.Regional bus operation bilevel programming model integrating timetabling and vehicle scheduling［J］.Systems Engineering-Theory ＆ Practice，2007，27(11):135-141.

［4］Haghani A，Banihashemi M.Heuristic approaches for solving large-scale bus transit vehicle scheduling problem with route time constraints［J］.Transportation Research，2002，36:309-333.

［5］Wang H，Shen J.Heuristic approaches for solving transit vehicle scheduling problem with route and fueling time constraints［J］.Applied Mathematics and Computation，2007，190:1237-1249.

［6］Li J Q，Mirchandani P B，Borenstein D.A heuristic for the real-time vehicle rescheduling problem［C］∥Transportation Research Part E，2009，45(3):419-433.

［7］Dennis Huisman，Albert P M.A solution approach for dynamic vehicle and crew scheduling［J］.European Journal of Operational Research，2007，172:453-471.

［8］Li J Q，Head K L.Sustainability provisions in the busscheduling problem［J］.Transportation Research Part D，2009，14:50-60.

［9］Bertossi A A，Carraresi P，Gallo G.On some matching problems arising in vehicle scheduling models［J］.Net-Works，1987，17(3):271-281.

［10］Ribeiro C C，Soumis F.A column generation approach to the multiple-depot vehicle scheduling problem［J］.Operations Research，1994，42:41-52.

［11］现代数学手册编纂委员会.现代数学手册:经济数学卷［M］.武汉:华中科技大学出版社，2000:307-369.

［12］钟磊钢，李云岗，张翠华.基于价格弹性的双层规划二级分销网络模型［J］.计算机集成制造系统，2006，12(10):1595-1599.Zhong Lei-gang，Li Yun-gang，Zhang Cui-hua.Bi-level programming secondary distribution network model based on price elasticity［J］.Computer Integrated Manufacturing Systems，2006，12(10):1595-1599.

［13］孙会君，高自友.考虑路线安排的物流配送中心选址双层规划模型及求解算法［J］.中国公路学报，2003，16(2):114-119.Sun Hui-jun，Gao Zi-you.Bi-level programming model and solution algorithm for the location of logistics distribution centers based on the routing problem ［J］.China Journal of Highway and Transport，2003，16(2):114-119.

［14］雷英杰，张善文，李续武，等.Matlab遗传算法工具箱及应用［M］.西安:西安电子科技大学出版社，2005:62-94.