混合型有源电力滤波器中输出滤波器的研究

童立青 孙耀杰 林燕丹 钱照明

(1.复旦大学信息学院 上海 200433 2.复旦大学先进照明技术教育部工程研究中心 上海 200433 3.浙江大学电气工程学院 杭州 310027)

1 引言

由于电力系统谐波污染的日益严重，有源电力滤波器（Active Power Filter，APF）是近十几年来被广泛用于电网谐波治理的一种有效方法。鉴于目前电力电子器件可控能量水平有限和电力系统要求控制能量巨大之间的矛盾，多样化方案和混合有源电力滤波器（Hybrid Active Power Filter，HAPF）是现阶段APF研究和应用的主要特征[1-4]。但当中仍然存在一些对HAPF性能有较大影响的参数和系统控制问题，输出滤波器（Output Filter，OF）就是其中之一。OF在HAPF中主要承担两种功能：滤除逆变器的开关纹波[5-7]和保证系统稳定可靠运行[8-13]。如果输出滤波器的参数设计不合理：①会使功率器件开关产生的高频谐波通过HAPF注入公用电网和用户端，影响到控制、通信设备以及精密仪器等的正常工作；②会使HAPF运行在不稳定区域而使系统不可靠，甚至导致系统故障；③会严重影响HAPF的补偿性能。

但是，文献[5-7]都仅从OF自身单个环节或与之相关的部分系统环节的特性来分析其在系统中作用和参数优化设计，而缺乏从系统整体和控制特性来考虑OF的性能。文献[8-13]从OF对系统的稳定性角度分析了OF的作用和参数设计，但文献[8-12]忽略了逆变器的死区效应、延时和控制环参数等的影响；文献[13]虽然从系统的闭环控制稳定性来分析和设计OF，但其所建立的控制模型，仅能定性描述而不能定量优化。虽然它们都提出了类似提高OF性能的改进方案，即增加OF阻尼电阻[5-6,13]，但在实际应用中，因阻尼电阻的损耗过大而影响经济性能，特别不适合高压大功率场合应用。

本文以串联有源电力滤波器（Series Hybrid Active Power Filter，SHAPF）[8]为例，从抑制逆变器开关纹波，控制系统稳定性和节约阻尼电阻损耗等来研究OF，在此基础上提出一种新型的OF阻尼控制策略。理论和实验结果都表明，该控制策略能降低有源部分损耗，有效抑制逆变器开关纹波，提高系统稳定裕度，是一种经济的、适合大功率APF应用的方法。

2 OF在抑制逆变器开关纹波中的作用

图1为电网和SHAPF的主电路结构图，主要有交流电网（包括短路电抗Ls）、有源滤波器、无源滤波器组和非线性负载四个部分。

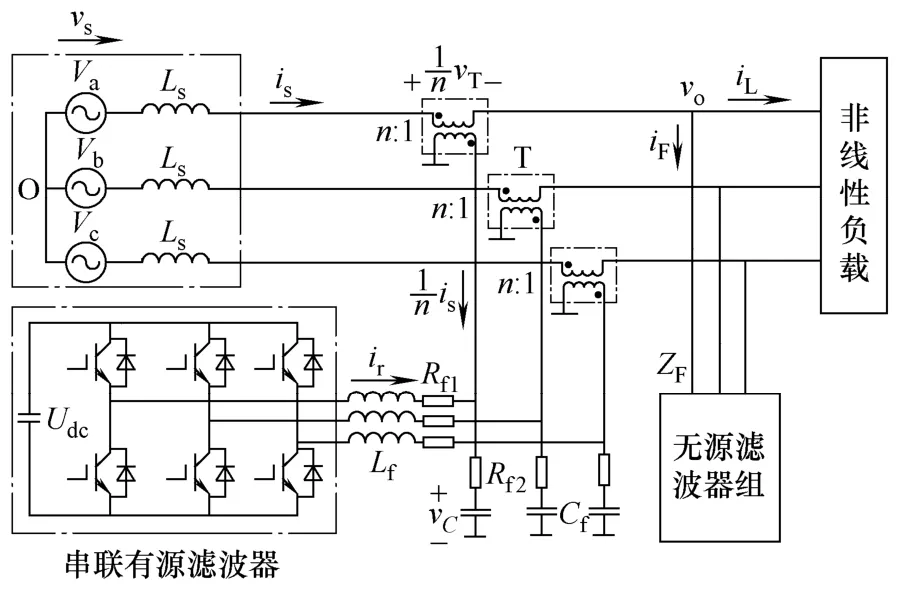
图1 串联混合有源电力滤波器系统结构图Fig.1 The SHAPF system configuration

图2 a为图1的单相等效电路，OF由Lf，Cf，Rf1和Rf2组成。图2b为OF滤波等效电路，逆变器开关纹波电压等效为Vr，ZPWM为电网侧阻抗Z（sLs）和ZF之和折合到耦合变压器二次侧的阻抗，即ZPWM=n2(Zs+ZF)，为防止开关纹波电流流入电网和有效抑制开关纹波电压，则对2fs频率的开关纹波需满足

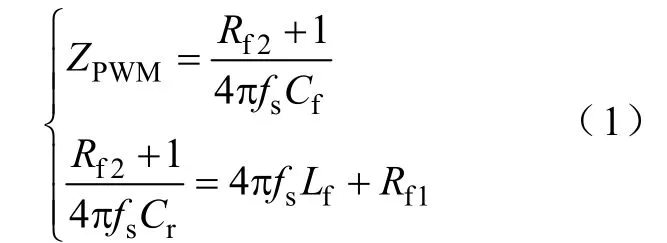
若OF满足式（1），则开关纹波电流将流入Cf支路，而开关纹波电压都将降在Lf支路上。

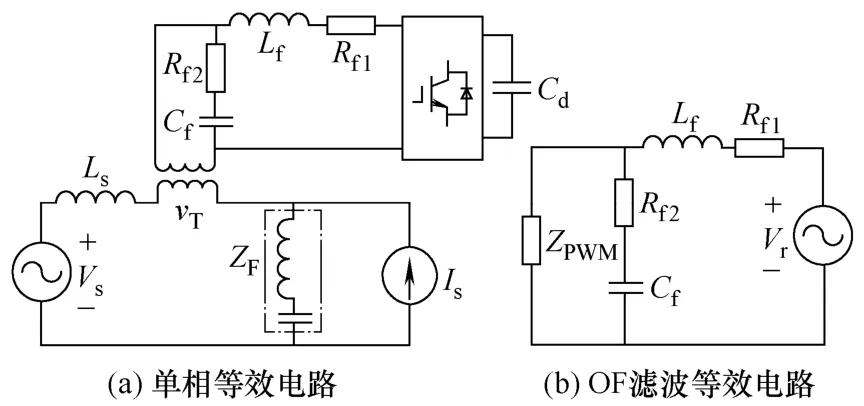
图2 开关纹波电压和电流抑制等效电路Fig.2 Equivalent circuit for switching ripples

3 SHAPF系统模型

要分析OF在SHAPF控制中的作用，研究其对闭环稳定性和滤波性能的影响，就必须要考虑电网、主电路和控制电路等每一个环节对系统控制性能的影响的基础上，建立准确的数学控制模型。

3.1 电网和SHAPF主电路模型

图3为SHAPF的串联有源部分的等效电路，逆变器的主功率器件采用IGBT模块，工作频率较高，利用状态空间平均法可以建立逆变器开关模型。

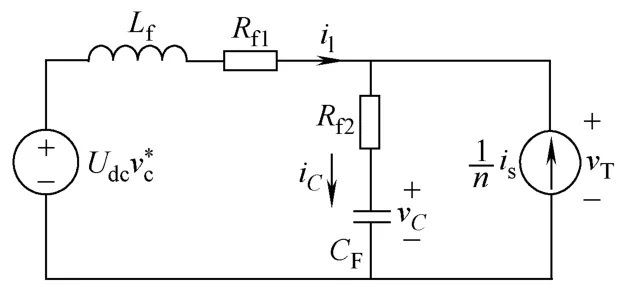
图3 SHAPF串联有源部分等效电路模型Fig.3 The equivalent circuit of the series active part for the SHAPF

当IGBT工作在开关状态时，逆变器输出电压可以表示为±Udc，根据状态空间平均法，IGBT状态可以表示为离散量U=[0,1]，则逆变器输出电压可以表示为Udc[2U-1]。根据双极性SPWM调制原理，离散输出量U可以表示为

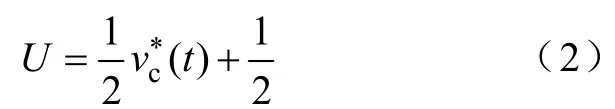
式中，vc*(t)是逆变器输入参考电压。闭环控制的串联有源滤波器输出电压vc经耦合变压器串入在电网主回路上。应用状态空间平均法可以建立SHAPF稳态状态空间模型如下：

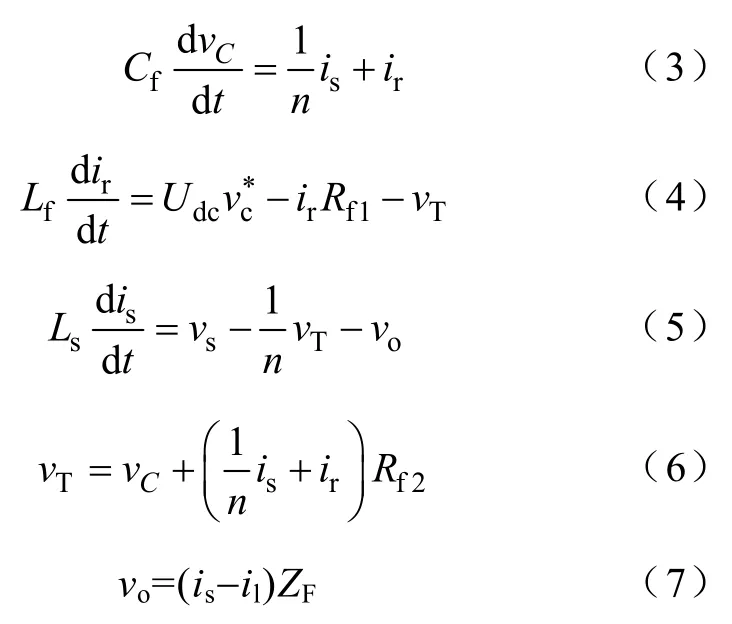
式中，is为电网电流；ir为电感Lf上的电流；il为负载电流；vC为电容Cf上的电压；vs为电网电压；vo为负载端电压；Ls为电网的系统阻抗；ZF为无源滤波器组阻抗；Rf1为Lf的本身内阻；Rf2为OF的阻尼电阻。则等效的状态空间模型为

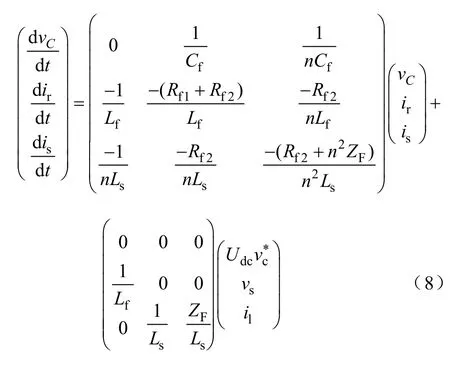
由式（8）可得有源滤波器输出电压VT为

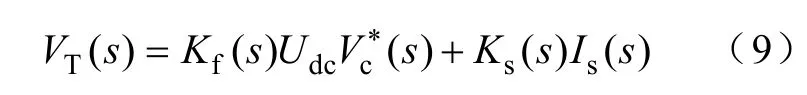
其中

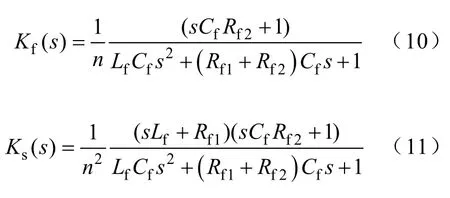
则由式（8）、式（10）和式（11）可得电网电流为

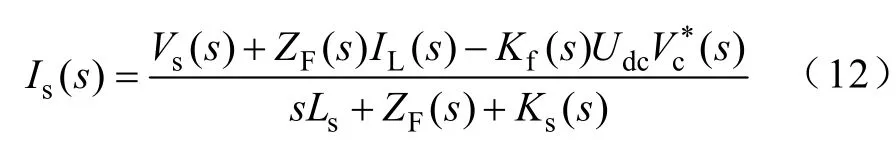
3.2 SHAPF控制电路模型

图4是SHAPF在传统控制策略下的等效控制框图，三相电网电流信号经同步旋转坐标变换（SRF）后可以提取电网谐波电流Ish(s)，Ish(s)经PI调节器和PWM脉宽调制后得到指令信号，同时考虑采样电路、控制延时和逆变器等的影响。

图4 串联式SHAPF控制框图Fig.4 The control diagram of the series-in SHAPF

图中，Kc为电流互感器及其调理电路的增益，(KPs+KI)/s为PI调节器，采用DSP数字控制方式，而采样电路和信号调制电路等控制电路延时都用一个集中的延时环节e-τs表示。一般在逆变器开关频率较高的控制系统中，Kv(s)可以近似看成是一个一阶惯性环节，最大的惯性时间常数为一个开关周期Tv[14]，则Kv(s)传递函数可以表示为

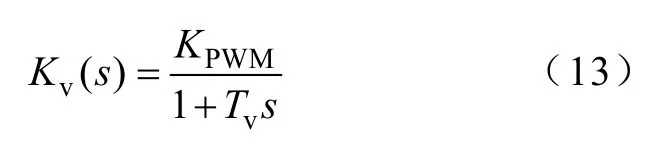
式中，KPWM为逆变器的调制比，则由图4可得控制回路的传递函数为

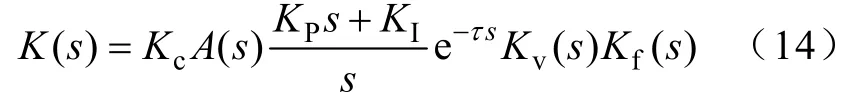
由文献[15]可得SRF谐波提取法的传递函数为

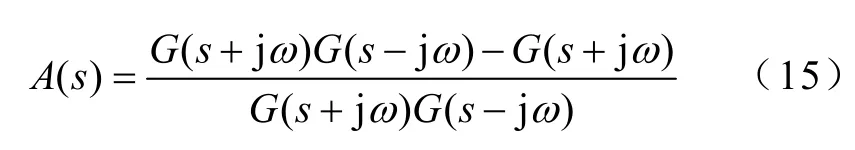
其中，1/G(s)为低通滤波器，具体表达式为

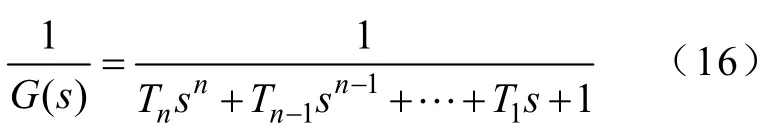
3.3 SHAPF系统模型

根据上述的状态方程的控制回路和逆变器环节，可得SHAPF传统控制策略下的闭环负反馈控制模型，如图5所示，则其开环传递函数为

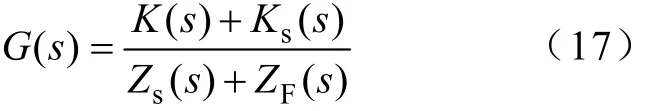
式中，Zs(s)为电网的系统阻抗，其值为sLs。因此可以根据SHAPF的闭环控制模型，研究系统的控制特性，判断系统的稳定性和OF等参数优化设计，也可以在保证系统稳定性的前提下设定最佳的开环增益K，提高系统的滤波性能，增大截止频率提高系统动态响应速度。

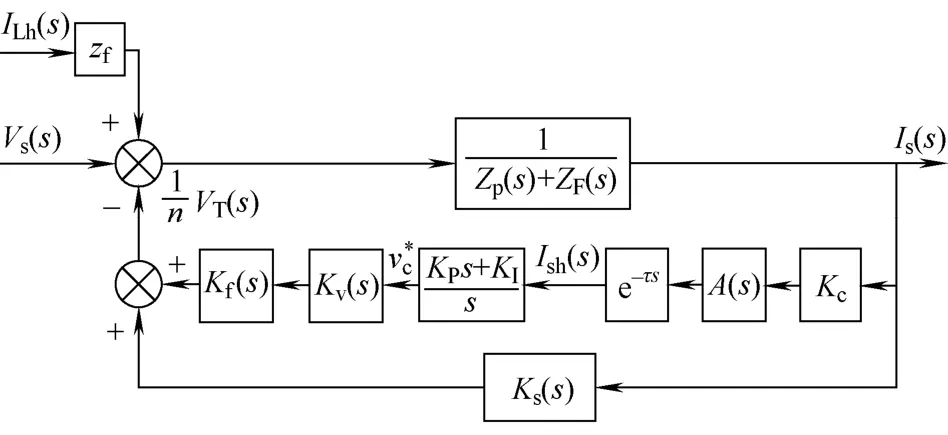
图5 SHAPF闭环控制模型Fig.5 The closed-loop model of the SHAPF

4 OF参数设计及影响分析

OF参数设计目标为：①有效抑制逆变器的开关纹波；②保证系统动态响应，截止频率fc≥1000Hz；③维持系统足够稳定裕度情况下获取最大的阻抗增益K。SHAPF固有的参数设定为：电网线电压为380V，容量为20kVA，系统感抗Ls为0.23mH；负载容量10kVA；并联的无源滤波器组（容量5kVA）与传统的无源滤波器组一样有5次、7次、11次LC串联谐振电路和高通滤波器，具体参数见表1。耦合变压器的电压比n为6，PWM逆变器的开关频率为20kHz，直流侧电压为150V。电压互感器及其调理电路增益Kc为0.238，设总延时τ为100μs，逆变器调制比KPWM为0.5。因此为满足OF参数设计目标①，根据式（1）和文献[5-6,13]提供的设计方法可得二阶OF的电感Lf为1.78mH（Q=30），则Rf1可以忽略不计，电容为9.4μF，阻尼电阻Rf2=10Ω；对于OF参数设计目标②，提高系统动态响应，使KI=0，可得fc≈1250Hz；而对于OF参数设计目标③，根据式（17），满足相位裕度≥40°，可得KP=3.79。

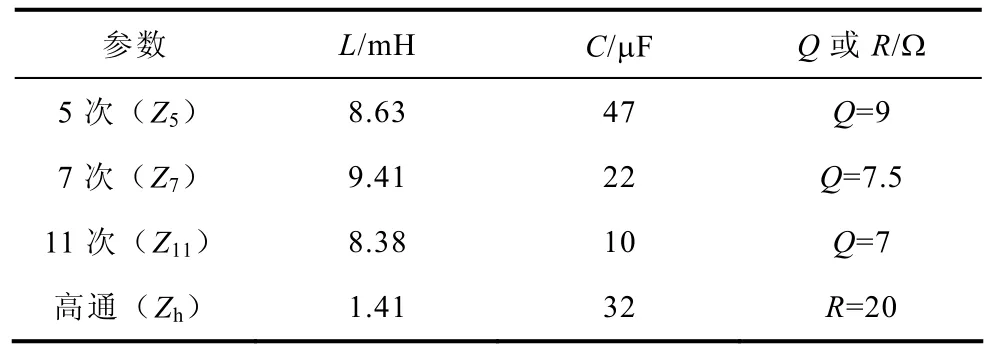
表1 无源滤波器组参数Tab.1 Shunt passive filters

上述设计中电阻Rf2值较大，必然增加损耗，限制SHAPF在大功率系统中应用[13]。而降低或者去掉电阻Rf2会影响系统的滤波效果，甚至使SHAPF系统不稳定，同时由图5可知OF参数对系统Kf(s)和Ks(s)都有着影响，它们的具体特性可分析如下。

对于Kf(s)传递函数，可转换表达成

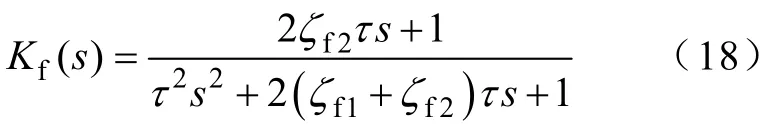
ζf1—电阻Rf1决定的内在阻尼比，可忽略；

ζf2—电阻Rf2决定的外加阻尼比。

不同的阻尼比ζf2情况下的Kf(s)的幅值和相位伯德图如图6所示，随着阻尼比ζf2的增大，谐振峰值幅值变小而相位增益变大。

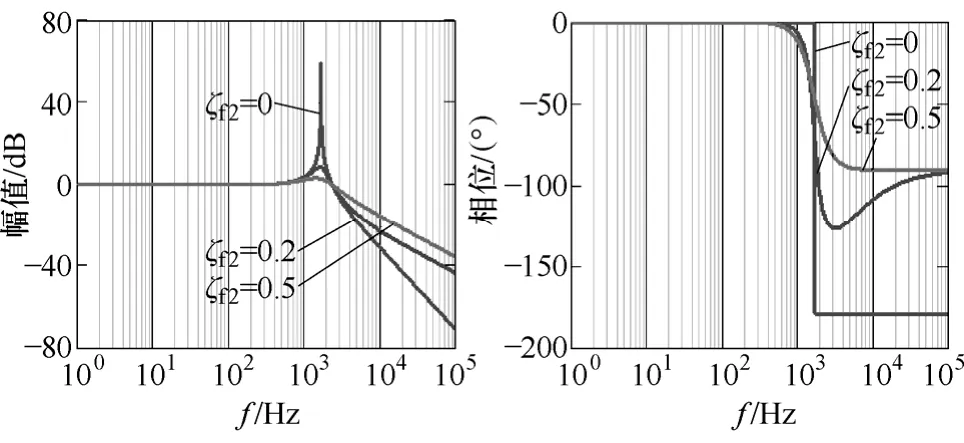
图6 在不同阻尼比ζf2下Kf(s)幅值和相位伯德图Fig.6 Magnitude and phase of the Kf(s) for different ζf2

同样Ks(s)的特性与Kf(s)类似，可以表示为

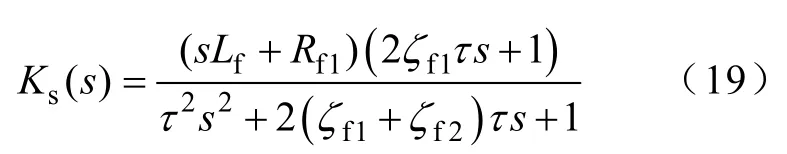
其幅值和相位伯德图如图7所示，当阻尼比ζf2较小时，有较大的谐振峰幅值，相位变化幅度较大，会影响系统在截止频率区的特性；而当阻尼比较大时，在高频区，幅值增益较大而相位变化不大，会对系统造成影响。由此可知不能根据Ks(s)和Kf(s)的特性来判断和确定OF在系统的控制特性。因此OF在SHAPF中的作用不仅要考虑其自身特性还要考虑其在整个系统中的影响，图8为不同阻尼比ζf2下整个SHAPF系统的幅值和相位响应伯德图。由图8可知：①随着ζf2的增大SHAPF开环传递函数的截止频率降低而相角增益增大，如：当ζf2=0时，截止频率fc1=1589Hz，相角裕度-57.54°；当ζf2=0.2时，截止频率fc2=1492Hz，相角裕度-12.74°；而当ζf2=0.5时，截止频率fc3=1000Hz，相角裕度达50.68°；②当阻尼电阻过大会导致系统截止频率变小，系统响应变差，阻尼电阻过小，系统稳定裕度不够。加大阻尼电阻Rf2方法可以提高系统稳定性和滤波性能，但会增加损耗，不适合高压大功率场合应用。

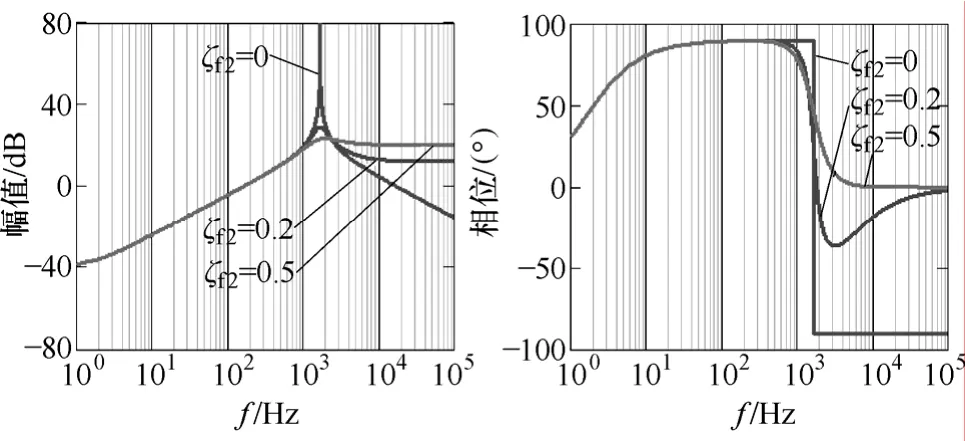
图7 在不同阻尼比ζf2下Ks(s)幅值和相位伯德图Fig.7 Magnitude and phase of the Kf(s) for different ζf2

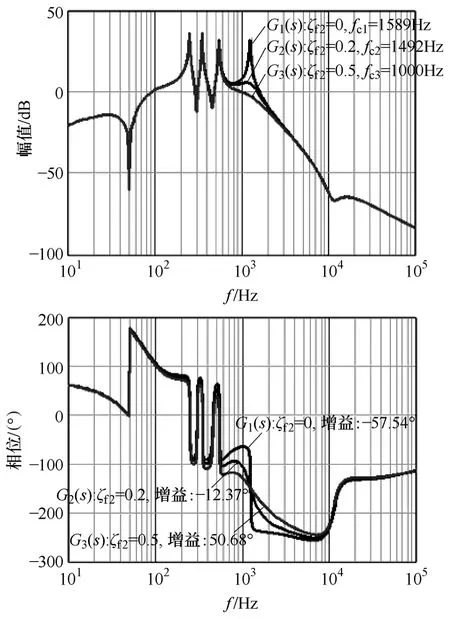
Fig.8 在不同ζf2下的G(s)的幅值与相位响应伯德图Fig.8 The Bode plot of G(s) with different ζf2

5 提出的新型SHAPF控制技术

为了降低阻尼电阻损耗，使SHAPF适合于高压大功率系统应用，本文利用微分负反馈增加二阶系统阻尼比的控制特性，提出在OF的输出侧，加一个微分负反馈环节来提高二阶系统阻尼比的控制策略，具体控制框图如图9所示。其具体实现方式为：采样有源滤波器输出电压VT，设H(s)=Kts，然后与谐波提取量相减，得系统开环传递函数变为

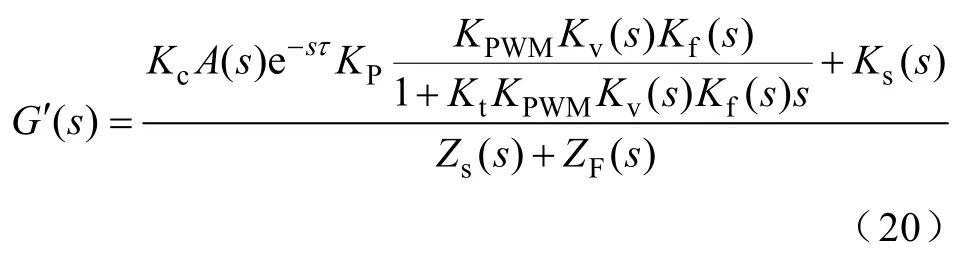
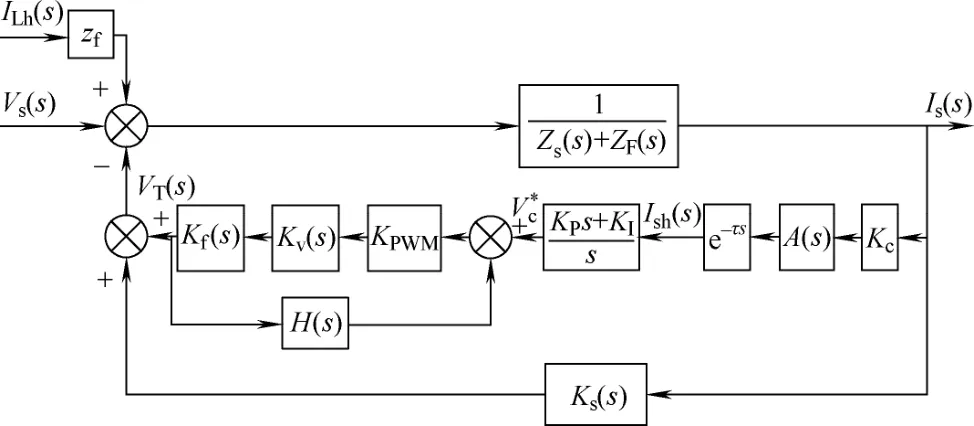
图9 提出的新型SHAPF控制策略Fig.9 The proposed control strategy for SHAPF

图10 为G′(s)的伯德图，当取Kt=9.6×10-6，由图可知，采用微分反馈环节后，不仅可以去除阻尼电阻，而且系统截止频率从G(s)的1589Hz变为G′(s)的1331Hz，相角裕度从-57.54°增加到42.37°。因此采用微分负反馈环节可以去掉阻尼电阻，相应提高系统动态响应，增加系统相角裕度，保证系统足够稳定裕度情况下降低阻尼电阻损耗。

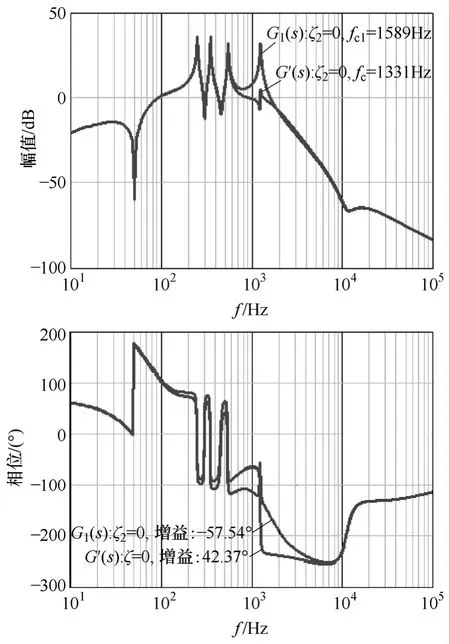
Fig.10 G1(s) andG′(s)幅值与相位响应伯德图Fig.10 The magnitude and phase Bode plot of G1(s) andG′(s)

6 实验结果

为了证实上述OF的理论分析和参数设计的正确性，本文根据图1制作了一套10kVA实验样机。实验具体参数如下：电网线电压为380V，容量为20kVA，测得系统感抗Ls为0.23mH；负载为三相不控整流桥感性负载，电感7.5mH，电阻25Ω；无源滤波器组参数见表1，耦合变压器的电压比n为6；主电路采用IPM电压源型逆变器（VSI）模块，开关频率为20kHz，直流侧的电容为1410μF，电压控制为150V；控制电路采用TI公司的TMS320LF2407A型号DSP控制芯片。采样及其调理电路增益Kc为0.238，采样频率为19.2kHz[15]，调制比KPWM为0.5；输出滤波器参数为文中的设计参数。图11为采用传统控制方法，阻尼电阻较大（Rf2=10Ω，KP=3.79）时的电网电流波形（THD=3.42%）和负载电流波形；图12为采用传统控制方法，阻尼电阻较小（Rf2=1Ω，KP=0.55）时的电网电流波形（THD=11.26%）和负载电流波形。从图11和图12可以看出，在传统控制策略下，当阻尼电阻较大时，电网电流波形较好，开环增益较大且系统稳定；当阻尼电阻较小时，电网电流波形较差，开环增益小且可能系统振荡甚至不稳定。图13为采用新型微分负反馈控制策略，无阻尼电阻（Kt=9.6×10-6，KP=3.79）时的电网电流波形（THD=4.51%），略微不如有阻尼电阻（大）时的滤波效果，但节省了阻尼电阻上的损耗，同时开环增益也较大。不管是图11传统加阻尼电阻控制策略，还是图13采用新型微分负反馈控制策略，它们的逆变器开关纹波都得到了有效抑制。三种控制策略下的实验结果及其性能比较见表2，从表2可知采用新型微分负反馈控制策略下的串联混合型有源电力滤波器更具有实用性。因此在中、小功率场合，应用电阻增加阻尼比可以获得较佳的滤波性能，而在大功率场合，本文提出的控制策略能获得一个经济的有源电力滤波器。

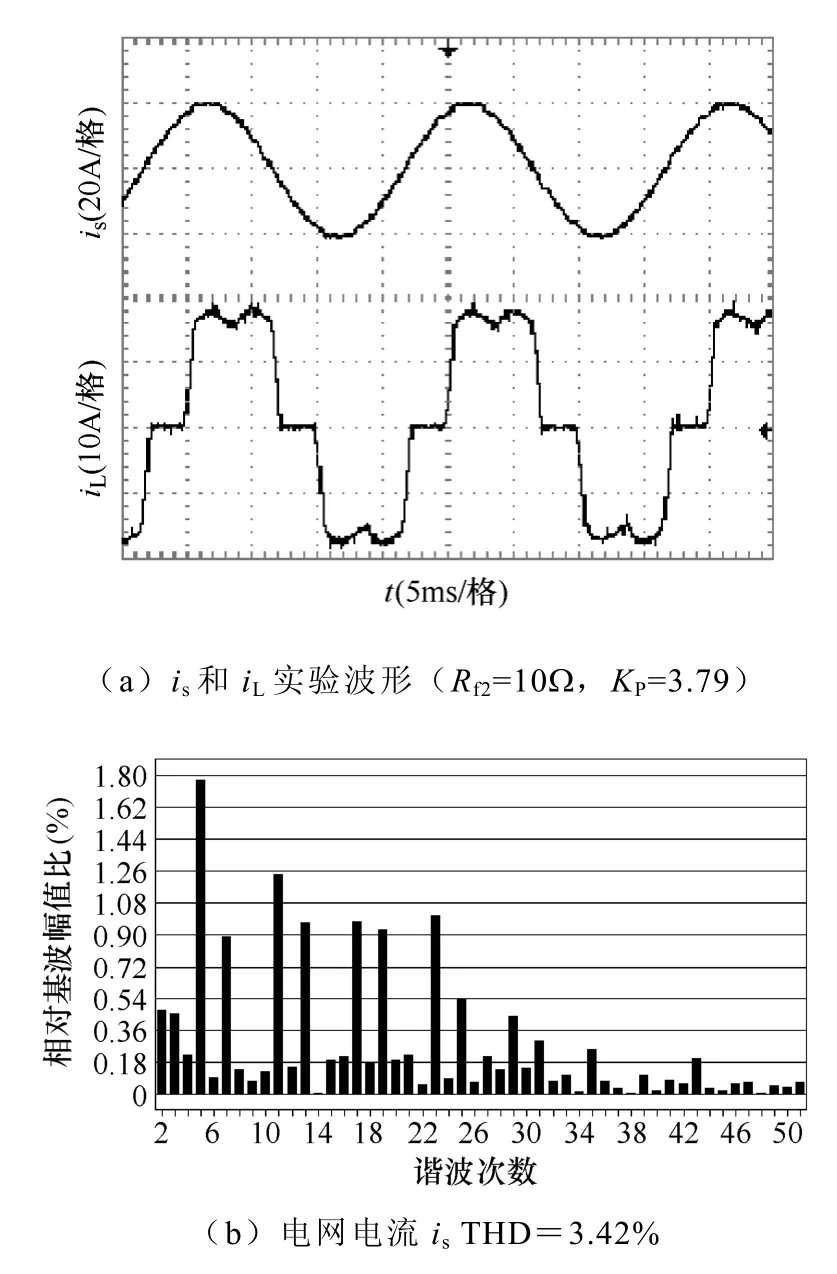
图11 大阻尼电阻，传统控制策略下的is和iL实验波形Fig.11 Experiment and comparison of iL and is with large damping resistor for the traditional control strategy

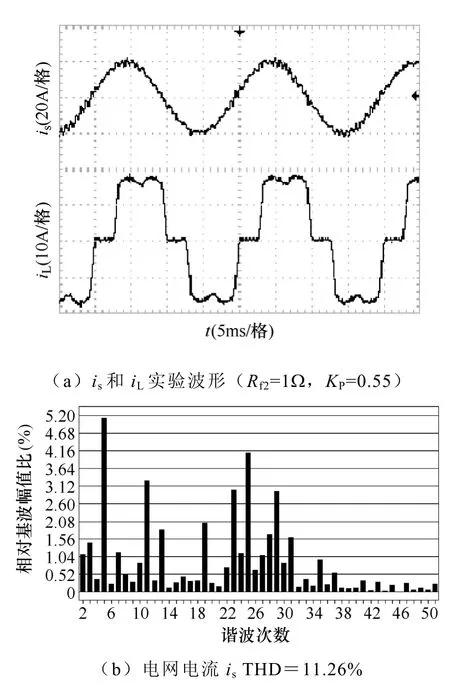
图12 小阻尼电阻，传统控制策略下的is和iL实验波形Fig.12 Experiment and comparison of iL and is with small damping resistor for the traditional control strategy

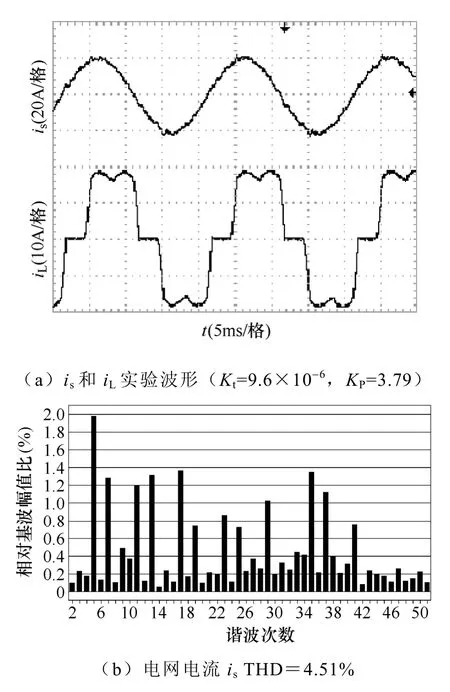
图13 无阻尼电阻，新型控制策略下的is和iL实验波形Fig.13 Experiment and comparison of iL and is with no damping resistor for the novel control strategy

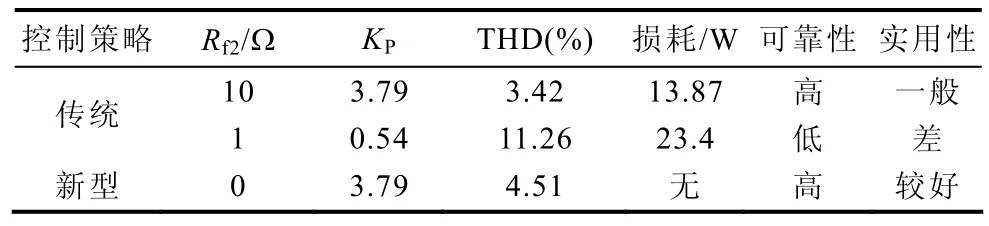
表2 不同控制策略下的性能比较Tab.2 Performance comparison on different control strategies

7 结论

本文首先分析了HAPF中OF抑制逆变器开关纹波和保证系统稳定可靠运行的功能，针对这两种功能，提出了新型OF参数设计方法和减少系统损耗的控制策略，其具有以下特点：

（1）更准确的OF参数值。①从整个系统的角度而不是分立的OF角度来进行设计；②定量（建立了整个系统准确的数学模型）地分析了OF对系统稳定性的影响，并对其进行参数优化设计。

（2）损耗更小。引入了微分负反馈而不是增加OF阻尼电阻的方式来提高OF的性能，消除了阻尼电阻的损耗。

[1] Singh B,Kamal Al-Haddad,Ambrish Chandra.A review of active filters for power quality improvement[J].IEEE Transactions on Industry Electronics,1999,46(5): 960-971.

[2] Ei-Habrouk,Darwish M ,Mehta P.Active power filter: a review[J].IEE Proceedings Electric Power Applications,2000,14(5): 403-413.

[3] Mariun N,Alam A,Mahmod S,et al.Review of control strategies for power quality conditioners[C].Power and Energy Conference,2004: 109-115.

[4] 汤赐,罗安,荣飞,等.混合型并联有源滤波器的设计及工程应用[J].电工技术学报,2007,22(6): 101- 107.Tang Ci,Luo An,Rong Fei,et al.Design and application of hybrid type shunt active filter[J].Transactions of China Electrotechnical Society,2007,22(6): 101-107.

[5] 史伟伟,蒋全,胡敏,等.串联型电力有源滤波器中低通滤波器的设计和参数优化[J].中国电机工程学报,2001,21(11): 74-78.Shi Weiwei,Jiang Quan,Hu Min,et al.Design and optimization of passive low-pass filters for series active power filters[J].Proceedings of the CESS,2001,21(11): 74-78.

[6] 涂春鸣,罗安.混合有源滤波系统中输出滤波器电感变化对系统性能的影响分析[J].电力系统及其自动化学报,2003,15(5): 54-58.Tu Chunming,Luo An.Effect of inductive variation in output filter on hybrid active power filter[J].Proceedings of the EPSA,2003,15(5): 54-58.

[7] 范瑞祥,罗安,章兢,等.谐振注入式有源滤波器的输出滤波器[J].中国电机工程学报,2006,26(5): 95-100.Fan Ruixiang,Luo An,Zhang Jing,et al.The output filter research of resonance injection active filter[J].Proceedings of the CESS,2006,26(5): 95-100.

[8] Peng F Z,Akagi H,Nabae A.A new approach to harmonic compensation in power systems-a combined system of shunt passive and series active filters[J].IEEE Transactions on Industry Applications,1990,26(6): 983-990.

[9] Peng F Z,Kohata M,Akagi H.Compensation characteristics of the combined system of shunt passive and series active filters[J].IEEE Transactions on Industry Applications,1993,29(1): 144-152.

[10] Peng F Z.Harmonic sources and filtering approaches[J].IEEE Transactions on Industry Applications,2001,7(4): 18-25.

[11] Peng F Z.Application issues of active power filters[J].IEEE Transactions on Industry Applications,1998,4(5): 21-30.

[12] 吴卫民,童立青,钱照明,等.新型串联混合有源电力滤波器控制技术的研究[J].中国电机工程学报,2005,25(3): 38-43.Wu Weimin,Tong Liqing,Qian Zhaoming,et al.A research on new control strategy for series type active power filter[J].Proceedings of the CSEE,2005,25(3):38-43.

[13] 陈国柱.混合有源电力滤波器关键技术的研究[D].杭州: 浙江大学,2001.

[14] 陈伯时.电力拖动自动控制系统[M].北京: 机械工业出版社,2005.

[15] Tong Liqing,Qian Zhaoming,Peng Fangzheng,et al.Optimal design of synchronous reference frame harmonic detection method[C].IEEE PESC,2007: 1071-1076.