电流型双向PWM整流器SPWM与SVPWM控制输出特性比较

康 伟 张丽霞 康忠健

（中国石油大学信息与控制工程学院 东营 257061）

1 引言

随着电流型整流器（Current Source Rectifier,CSR）在超导储能[1]，静止同步补偿器（STATCOM）[2]等场合的广泛应用，电流空间矢量脉宽调制（SVPWM）和正弦脉宽调制（SPWM）作为两种常用的变流调制方式也得到了日益广泛的研究和应用。SVPWM是将二相变流器的指令输出电流在复平面上合成为电流空间矢量，并通过不同的开关矢量组合去逼近指令电流空间矢量。有资料表明，作为AC-DC整流器使用时，与传统的SPWM相比，SVPWM开关器件的开关次数可减少1/3，直流电压的利用率可提高15%，能获得较好的谐波抑制效果，因而多数应用场合更倾向于使用SVPWM作为脉冲控制策略。然而本文将电流型PWM整流器用于有源逆变时，却得到了完全相反的结论。

关于电流型SVPWM输出定量分析的文献较少，多为电压型的。但从二者电路结构的对偶性，也可借鉴结论作为理论的参考[3]。文献[4]从逆变器控制方程的解的角度，详细分析了电压型空间矢量调制SVPWM和三角载波调制SPWM的关系，得出两者的本质联系在于它们是同控制方程在不同附加条件下的两个不同的特解。文献[5]从发生原理和数字实现对电压型SVPWM和SPWM进行了深入分析，通过数学计算推导得到了虽然3P3W系统中SVPWM在谐波抑制和直流电压利用率上均优于SPWM，3P4W系统中电压型SPWM和SVPWM的归一化，但在3P4W系统中两者从控制效果上看是一致的结论等。以上均可作为电流型SVPWM输入输出定量分析的思路。

本文基于根据指令电流产生触发脉冲时SPWM和SVPWM的不同机理，以能量传输和面积等效原理为依据，分析了电流型SPWM和SVPWM逆变输出交流电流量值的不同，并根据所得结论设计了电流型PWM双向整流器提高整体电流利用率的控制方法。

2 SPWM和SVPWM的比较

考虑到控制系统的快速响应能力，以直接电流控制为例，电流型PWM双向整流器的双闭环控制结构如图1所示[6]。

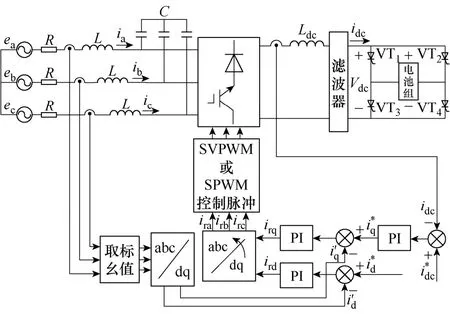
图1 CSR直接电流控制原理框图Fig.1 Direct current control strategy of CSR

无论SPWM还是SVPWM，在进行从指令电流到控制脉冲转换之前，双闭环的工作原理是相同的。其外环为直接电流控制环，外环调节器的输出iq*为内环有功电流指令。将三相静止对称坐标系（a，b，c）下交流侧电流ia，ib，ic取标幺值后经过abc-dq0转换得到同步旋转坐标系（d，q，0）下的id′和iq′；分别将id′与无功分量指令id*，iq′与有功分量指令iq*相比较，经过调节器得到无功分量ird和有功分量irq。当CSR工作在单位功率因数时，其无功分量指令给定值id*为零，有功分量指令iq*由外环调节器输出。外环控制的目的是保持直流侧电流idc恒定；内环电流控制的目的是要求网侧电流在d-q坐标系中的分量id和iq始终跟踪指令电流id*和iq*，实现单位功率因数及低谐波电流控制。当工作在整流状态时，SVPWM与SPWM相比，电流利用率提高了约15.5%，此结论文献[7]已做了详细描述，在此不复论证。本文仅分析SPWM和SVPWM工作在逆变时的输出特性。

由于电路结构的原因，CSR电流方向不能改变。工作在逆变状态时需要两个条件：①将直流侧的电池电压反相以得到负值的电源（如图1中所示的晶闸管VT1～VT4：当CSR工作于整流状态时，VT1和VT4开通，工作于逆变状态时，VT2和VT3开通，以获得反向的压源）；②电池端电压需高于CSR的直流侧输出电压。

2.1 直流电流输出量值的比较

这里特别指出的是，对于CSR，运行于双闭环控制时，决定其逆变电流大小的实际上是其指令电流的幅值（本文指标幺值）。因此本文分析当指令电流的幅值一定时，电流型SPWM和SVPWM输出调制波对应交流侧输出电流幅值大小。

CSR工作于逆变状态时，假设直流电压源（如动力蓄电池组，太阳能电池组等）输出电压为Ue，整流器经滤波元件后输出电压为Ee，电池组的内阻为Re，则电池组的放电电流为

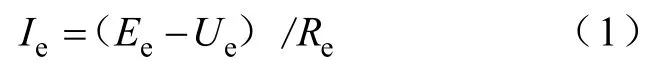
设SPWM输出电压为Ue1，输出电流为Ie1；SVPWM输出电压为Ue2，输出电流为Ie2。当整流器工作于恒功率时，二者输出电压与输出电流乘积为定值，即有

2.1.1 SPWM放电电流

设三相CSR直流侧电流为定值Idc，根据三值逻辑PWM控制规律，三相CSR交流侧电流ikt（k=a,b,c）可表示为

则三相CSR a相交流侧电流iat满足

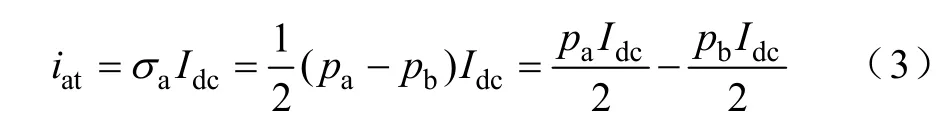
式中，pa、pb=±1为双极性二值逻辑开关函数。

三相CSR a相电流是由a、b两相相应的基于二值逻辑的PWM差值所构成。由于pa为二值逻辑开关函数，则pa可由三角载波PWM生成。考虑三角波两个负峰值之间为一个载波周期，另外设调制信号uma与三角载波信号ut的交点相位角分别是θ1和θ2，令a相调制信号为uma=msin(ωs+φ)，b相调制信号为umb=msin(ωs+φ-2π/3)，则可求得三相CSR的a相电流基波分量为

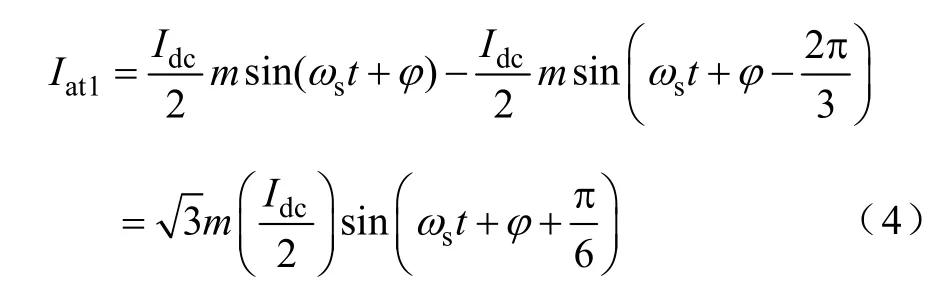
则三相CSR三角载波PWM直流放电电流与交流侧基波电流的峰值之比为

2.1.2 SVPWM放电电流

当三相CSR采用空间电流矢量PWM控制时，若以单三角的矢量合成模式为例，如图2所示。

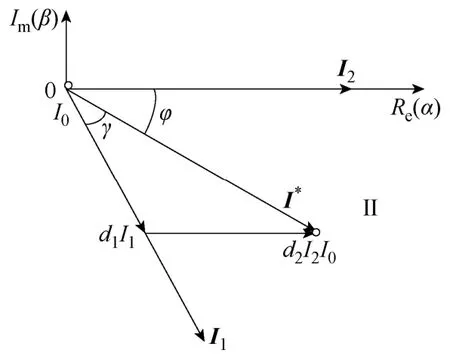
图2 单三角模式电流矢量的合成Fig.2 Current space vector modulation by single triangulation schema

设I*位于区域VI，假设矢量I*与I1夹角为γ，则有

由三角正弦定理得

式中

I1、I2的施加时间T1、T2分别为

式中

将式（8）和式（9）代入式（6），根据三角变换公式可以推得如果指令电流矢量为I*，当开关频率足够大时，合成的矢量I*=|I*|ejφ。

由于调制过程必须满足T1+T2＜Ts，则将式（7）代入式（10）得

若对于任一相位角γ式（11）均要成立，则

式（11）表明，当三相CSR采用空间电流矢量PWM控制时，其交流侧电流基波峰值It1m最大取值为Idc，则三相CSR空间电流矢量PWM直流放电电流与交流侧基波电流的峰值之比为

则有源逆变时，SPWM与SVPWM输出电压

能够达到的实际输出电流（即电池放电电流）根据公式Ie=(Ee-Ue)/Re可得到两个重要结论：①在相同指令电流（即相同的调制比m）的前提下，SPWM输出逆变电流大于SVPWM，其电流大小取决于整流器直流侧输出电压，电池端电压以及电池内阻；②CSR工作于逆变状态时，无论SPWM还是SVPWM，充电电流均随m的增大而增大；放电电流均随m的增大而减小。

2.2 SPWM和SVPWM二者指令电流的联系

根据载波与调制波的联系，开环运行时，如果两者具有相同的调制比m，则SVPWM输出的马鞍形调制波与SPWM输出的正弦调制波具有相同的幅值。

参考图1，两者的指令电流均为调节器输出的无功分量ird和有功分量irq经dq反变换得到。因此，如果两者的ird和irq分别相同，那么它们的三相指令电流大小相等，相位相同。

双闭环运行时，为达到网侧功率因数为1，无功的给定id*为零。但此时ird和irq都是经PI调节器输出，反馈量id′不一定为零，因此与之相对应的PI调节器的输出ird也不为零，即使最终逆变器输出达到稳态PI的调节也是一个动态的过程，则逆变器输出电流的大小取决于最终调制波幅值对应的调制比m。

3 新的控制策略

根据上面的理论分析可知，当变流器工作在整流方式时，使用SVPWM控制策略具有较高的效率，而当变流器工作在逆变方式时，SPWM方式具有更高的放电效率，据此本文提出了一种电流型双向变流器的控制策略，即当CSR工作于整流状态时采取SVPWM控制策略而有源逆变时采取SPWM控制策略，可以得到更大的输出电流和更高的电源利用效率。

3.1 仿真研究

为了验证本文提出的控制策略，使用Matlab搭建了CSI模型，并分别使用SVPWM和SPWM两种控制策略进行了仿真。图3所示为当指令电流幅值为1时，利用Matlab软件生成的SPWM和SVPWM调制波的波形。

图3 幅值为1时SPWM和SVPWM的调制波Fig.3 Modulating waveforms of SPWM and SVPWM when there amplitudes are 1

当SPWM与SVPWM的三相指令电流大小相等、相位相同时，由于SPWM的指令电流为正弦波，而SVPWM的指令电流为马鞍波，则其调制波对应的面积不等，马鞍波面积大于正弦波。由图3推得：分别采用同幅值的马鞍波与正弦波作为调制波时，其输出电流不相等。那么双闭环控制输出相同的idc，利用两种不同的控制策略采取的指令电流不再相同；即二者输出的无功分量ird和有功分量irq不同，SPWM的有功分量绝对值较大（即对应的m较大）。

图4所示为双闭环直接电流控制CSR，交流电源峰值电压100V，电池电压52V，指定直流放电电流40A时SPWM和SVPWM输出的无功分量ird和有功分量irq的比较。其输出指令电流的数值，SPWM为0.5，SVPWM为0.432。图4验证了图3的推论：相同条件下，SVPWM输出相同的逆变电流时，采用的调制比m较SPWM的小。随着m的减小，SVPWM将首先达到输出的极限。因此在逆变时，SPWM具有比SVPWM更宽的电流输出范围。

图4 两种控制策略输出无功分量ird和有功分量irqFig.4 Output reactive component ird and active component irq of two control strategies

电流型逆变器是通过输出反向电压得到逆变状态。从理论上来说，其指令电流I*（标幺值）相对越小，输出电流越大。当I*=0时，其输出电流达到最大，此时相当于电池组被短接。实际上，作为直流电源的电池组都有其极限输出功率，因此理论上的最大输出电流是无法得到的。图5为在Matlab仿真环境中，交流侧实测功率为负的前提下，当SPWM和SVPWM的指令电流I*=0.8时，二者的逆变电流。可见在相同条件下，SPWM比SVPWM输出较大的逆变电流。

图5 I*=0.8时SPWM与SVPWM的逆变电流Fig.5 Inverting current of SPWM and SVPWM

3.2 实验

为了进一步对本文提出的理论进行验证，在实验室利用TI公司的32位DSP芯片TMS320F2812搭建了实验平台，并进行了实验验证，实验结果如下。

图6所示为当指令电流幅值为1时，利用DSP生成的SPWM和SVPWM调制波的波形。根据仿真结果（图3）可知二者调制波对应的面积不等，马鞍波面积大于正弦波。根据面积等效原理，同幅值、相位的马鞍波与三角波相交得到的脉冲面积大于正弦波。当整流时，实际充电电流Ie=(Ue-Ee)/Re，放电电流Ie=(Ee-Ue)/Re，因此二者指令电流相同时，整流时SVPWM输出电流较大，而逆变时SPWM输出电流较大。

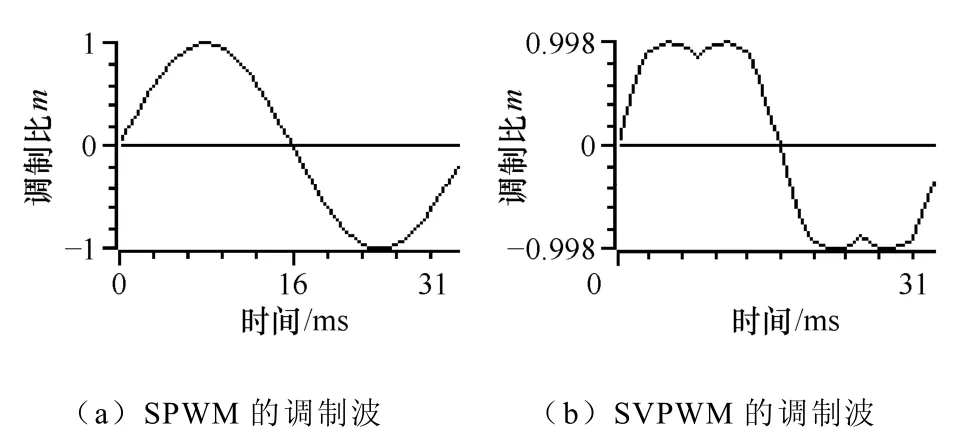
图6 指令电流幅值为1时DSP生成的调制波Fig.6 Modulating waveforms of SPWM and SVPWM output by DSP

限于篇幅，本文仅给出CSR分别采用SPWM和SVPWM双闭环控制，对一节60A·h/12V的汽车电池进行充电、放电，同时检测网侧电流波形。整流时调压器输出为23.8V，电池端电压12.3V；逆变时调压器输出线电压18.9V，电池电压12.4V；开关频率为1.6kHz。实验时调节直流给定i*dc，观察并记录CSR的最大输出，结果分别如图7和图8所示。

由图7，图8可以看出，当CSR工作在整流状态时SVPWM比SPWM输出更高的充电电流；而工作在逆变状态时SPWM能够比SVPWM输出更高的逆变电流。两者的优点因为直流侧电池组是反电势负载而更加突出，如本实验中，SVPWM在充电时电流是SPWM的1.5倍，而SPWM在放电时，放电电流是SVPWM的2倍。当然该倍数关系不是确定的，它的数值取决于CSR网侧电压、电池组端电压以及电池组内阻的取值。

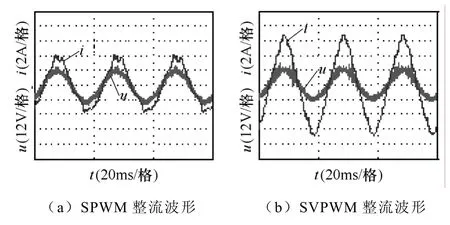
图7 SPWM和SVPWM整流器网侧波形Fig.7 Waveforms of grid side of the two rectifiers

图8 SPWM和SVPWM逆变器网侧波形Fig.8 Waveform of grid side of the two inverters

以上实验波形证明了有源逆变时SPWM比SVPWM具有更高的电流利用率。本实验的波形不是十分理想。其原因主要是电源三相不平衡，且变压器存在饱和的现象。经测试发现实验室电源存在严重的三相不平衡的情况。研究表明三相不平衡时三相电流型PWM整流器直流电压会产生6、12、18等6的整数倍的特征谐波和2、4、8、10等次的非特征谐波。直流电压谐波导致整流器产生直流电流谐波，直流电流谐波通过PWM反过来又会影响整流器的交流电流波形，即三相电流型PWM整流器直流侧n次谐波电流经PWM控制后，将在整流器交流侧产生n+1次谐波电流[8]。

对于电网电压不平衡状态下，可以通过适当控制三相电流型PWM整流器抑制二次谐波，目前已有针对电压型PWM抑制直流侧二次谐波的研究[9-10]，但适用于电压型PWM整流器的方法有待于借鉴到电流型PWM整流器中。

4 结论

本文基于SPWM和SVPWM根据指令电流产生触发脉冲的不同机理，以能量传输和面积等效原理为依据，对电流型SPWM和SVPWM逆变输出交流电流量值进行了比较。通过分析得出SPWM工作于逆变状态时能够比SVPWM输出更大的放电电流的结论，据此提出了整流时使用SVPWM而在逆变时使用SPWM的控制策略，以获得最大的电流利用率，并通过仿真和实验验证了结论的正确性，为电流型PWM双向整流器的控制策略提供了新的思路。

[1] 彭晓涛,程时杰,王少荣,等.一种新型的电流源型变流器PWM控制策略及其在超导磁储能装置中的应用[J].中国电机工程学报,2006,26(22): 60-65.Peng Xiaotao,Cheng Shijie,Wang Shaorong[J].A novel PWM control for current source converter and its application in a superconducting magnetic energy storage unit[J].Proceedings of the CSEE,2006,26(22): 60-65.

[2] Wang Bingsen,Cathey Jimmie J.DSP-controlled,space-vector PWM current source converter for STATCOM application[J].Electric Power Systems Research,2003,67(2): 123-131.

[3] 陈国呈.PWM逆变技术及应用[M].北京: 中国电力出版社,2007.

[4] 周卫平,吴正国,唐劲松,等.SVPWM的等效算法及SVPWM与SPWM的本质联系[J].中国电机工程学报,2006,26(2): 133-137.Zhou Weiping,Wu Zhengguo,Tang Jinsong,et al.A novel algorithm of SVPWM and the study on the essential relationship between SVPWM and SPWM[J].Proceedings of the CSEE,2006,26(2): 133-137.

[5] 陈瑶,金新民,童亦斌.三相四线系统中SPWM与SVPWM的归一化研究[J].电工技术学报,2007,22(12): 122-127.Chen Yao,Jin Xinmin,Tong Yibin.Study of the unification of SPWM and SVPWM in three-phase four-wire systems[J].Transactions of China Electrotechnical Society,2007,22(12): 122-127.

[6] 张丽霞,颜湘武,康伟,等.基于空间电流矢量的动力蓄电池组测试系统变流技术研究[J].电工技术学报,2010,25(9): 122-128.Zhang Lixia,Yan Xiangwu,Kang Wei,et al.Converting technology based on the current mode SVPWM on the power accumulator battery testing system[J].Transactions of China Electrotechnical Society,2010,25(9): 122-128.

[7] 张崇巍,张兴.PWM整流器及其控制[M].北京: 机械工业出版社,2003.

[8] 李玉玲.电流型PWM整流器及其控制策略的研究[D].杭州：浙江大学，2006.

[9] 荣飞,罗安,范卿.应用于不平衡系统的STATCOM电压控制新方法[J].电工技术学报,2010,25(3): 138-143.Rong Fei,Luo An,Fan Qing.A novel voltage control method applied in STATCOM under unbalanced system[J].Transactions of China Electrotechnical Society,2010,25(3): 138-143.

[10] 金爱娟,李航天,李少龙.基于单周期控制的三相PFC整流器在输入电压不对称时的改进策略[J].电工技术学报,2006,21(7): 115-120.Li Aijuan,Li Hangtian,Li Shaolong.An improved control strategy of the one cycle control three-phase PFC rectifier under unbalanced conditions[J].Transactions of China Electrotechnical Society,2006,21(7): 115-120.