在线自适应PWM死区消除方法
杨 波 吴建德 李武华 何湘宁
(浙江大学电气工程学院 杭州 310027)
1 引言
对于脉冲宽度调制(PWM)的电压源型逆变器(VSI)而言,由于实际开关器件的开关动作都需要一定的时间,因此为了防止同一桥臂上下两个开关器件产生“直通”现象,通常需要在互补的驱动信号之间加入一个死区时间。死区是为了保证开关器件安全、可靠运行而不得不采取的措施,但它的存在将导致逆变器输出产生基波电压损失、低次谐波增加、输出电流畸变等死区效应[1-5]。随着现代器件开关频率的不断提高,死区效应对逆变器输出电压和输出电流的影响也越来越严重,因此,对逆变器的死区进行消除和补偿变得更为重要。
目前,国内外专家学者已经提出了大量的死区消除和补偿方法[6-15]。一类属于死区补偿方法,即从控制的角度出发,将死区产生的谐波视为外部扰动,应用各种反馈或前馈的控制算法,抵消死区效应。这类方法包括平均电压补偿法、预测电流控制补偿法、自适应控制补偿法、扰动观测器补偿法等等[6-11]。但由于死区效应和开关器件都具有非线性的特点,这类控制补偿的方法很难完全消除死区带来的谐波。另一类属于死区消除方法,即从死区产生的原理出发,根据输出电感电流方向的不同,只允许同一桥臂中相应的一个开关器件进行开关动作,从而避免了“直通”现象的产生,不再需要设置死区时间[12-15]。但由于电感电流纹波受电感大小影响,同时无论利用模拟电路还是模-数转换器(ADC)进行的电流过零点检测均会受采样精度和采样延时的影响,使得用于电流方向判定的过零点检测具有较大的模糊性,因此理论的电感电流过零点实际是一个具有一定宽度的区域,该过零区域宽度的检测和计算受到相应算法精度的约束。在此过零区域中,为了让逆变器正常工作,一般采用恢复同一桥臂上下两个开关器件的驱动信号并重新加入死区的策略[14-15]。死区在电感电流检测过零区域的注入,将导致逆变器输出在该区域产生明显的波形畸变。同时检测器件的特性和可靠性极大地影响了该类方法的有效性。
为了解决上述问题,本文提出一种在线自适应的PWM死区消除方法,该方法通过在线跟踪负载变化,自适应地计算最优的电感电流过零区域宽度,以精确实现电感电流过零区域和非过零区域死区效应的分别消除,从而使逆变器输出在整个正弦调制周期内无论负载如何,均能有效消除死区,明显减小输出电压基波损失和低次谐波含量。同时,本文引入的自适应算法对电流采样器件的特性和精度要求大大降低,有效地提高了该死区消除方法的实用性和系统的可靠性。
2 死区效应分析
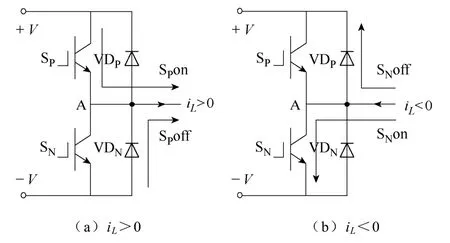
图1 电压源型逆变器单桥臂结构示意图Fig.1 Single phase-leg configuration of VSIs
图1 是电压源型逆变器单桥臂的结构示意图,其中图1a和图1b分别表示电感电流不同方向时桥臂内功率器件的导通情况。当iL>0时,SP开通,电流iL从SP流过;SP关断,iL通过VDN续流,无论SN开关状态如何,均无电流流过。同理,当iL<0时,SN开通,电流iL从SN流过;SN关断,iL通过VDP续流,无论SP开关状态如何,均无电流流过。
为了防止桥臂内功率器件SP和SN产生“直通”现象,传统的控制方式是在它们的驱动信号之间加入死区,因此产生死区效应。图2是电压源型逆变器输出电压的死区效应示意图,其中SP和SN表示单桥臂内上下两个开关管在理想情况下互补对称的驱动波形,SP′和SN′表示加入死区后的实际驱动波形,UAN和UA′N表示单桥臂的理想输出电压和实际输出电压波形,Ud表示由于死区注入后导致的理想输出电压和实际输出电压之差,即死区效应产生的死区电压波形。
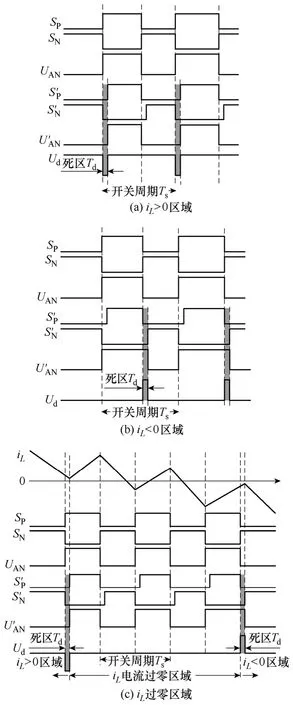
图2 输出电压死区效应分析示意图Fig.2 Dead-time effects on output voltage
由图2可见,在iL>0区域,死区效应给逆变器输出电压注入了一个以开关频率为频率,死区时间为宽度,母线电压为幅值的负值周期性脉冲电压;同理,在iL<0区域,死区效应注入的是相应的正值周期性脉冲电压;而在iL过零区域,由于正负相消,没有死区效应的产生。根据高频小纹波近似理论,在一个正弦调制周期T内的平均死区电压<Ud>的波形如图3所示,幅值大小为

式中fs——开关频率;
Td——死区时间;
Udc——直流母线电压。
显然,呈周期方波特性的死区电压将导致逆变器输出电压跌落和低次谐波注入。
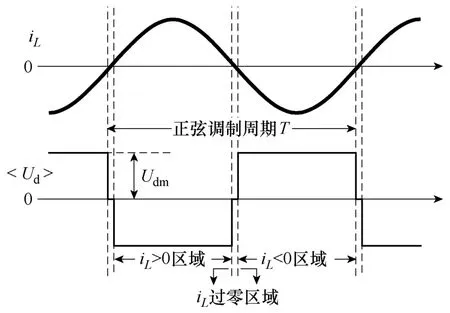
图3 正弦调制周期内的平均死区电压波形Fig.3 Average dead-time voltage waveforms in period T
3 死区消除原则
3.1 电流非过零区域死区消除原则
由图1分析可知,当iL>0时,无论开关器件的驱动信号如何,电流只流过开关管SP或二极管VDN,而开关管SN和二极管VDP绝不会有电流通过,因此将SP和VDN称为在iL>0阶段的有效器件,SN和VDP称为无效器件;同理,在iL<0阶段,SN和VDP成为流通电流的有效器件,SP和VDN为无效器件。显然,在电流非过零区域,同一桥臂内导通电流的有效器件只可能是一个全控型的开关管和一个不控型的二极管,因此,只要屏蔽相应阶段无效开关管的驱动信号,则死区可以被完全消除,进而有效地减小了输出电压基波损失和低次谐波含量。
3.2 电流过零区域死区消除原则
由前分析可知,一方面,在电流iL过零区域,由于电感电流纹波的存在,以及受采样精度和采样延时的影响,检测到的电感电流过零点将分布在一个具有一定宽度的区域内,该区域的宽度被称为过零检测宽度。在此检测宽度内,为了让逆变器能够正常工作,必须恢复同一桥臂上下两个开关器件的驱动信号,并重新加入死区。
另一方面,由图2c分析可知,在电流iL过零区域,同时存在一个过零理论宽度,在此理论宽度内,即使死区时间存在,也由于正负相消,没有死区效应的产生。因此,如果过零检测宽度能够完全与过零理论宽度重合,则该区域内的死区效应也完全被消除。
3.3 过零误差宽度和过零宽度系数
显然,由于电流检测精度和延时受检测手段的影响,过零检测宽度不可能正好等于过零理论宽度,定义两者之差为过零误差宽度。过零误差宽度的存在,会导致上述死区消除方法无法在整个正弦调制周期内完全消除死区效应。如果检测宽度大于理论宽度,则在过零误差宽度内重新引入死区电压,从而导致输出电压波形畸变和低次谐波的引入;如果检测宽度小于理论宽度,则在过零误差宽度内破坏了原有的电流流向,改变了正常的PWM调制方式,同样导致输出电压波形畸变和低次谐波的引入。
图4所示是上述死区消除方法的示意图,为分析由过零误差宽度引入的谐波含量,定义过零检测宽度为Tft,过零理论宽度为Tth;并定义过零误差宽度Tderr和过零宽度系数KZ如下:
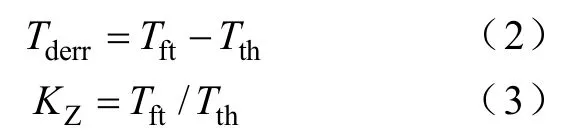
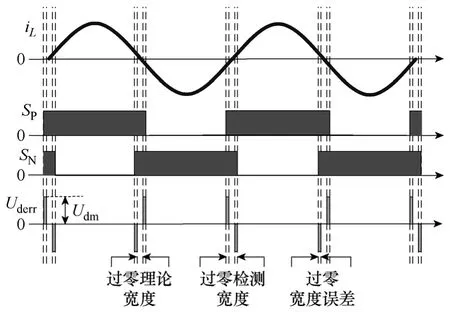
图4 死区消除原则示意图Fig.4 Principle of dead-time elimination
图5 是由过零误差宽度Tderr引入的死区电压Uderr的频谱分析图。设Udc=400V,fs=20kHz,Td=2μs,Tth=1.5ms,由式(1)得Udm=16V。显然,过零误差宽度Tderr的绝对值越小,过零检测宽度就越接近过零理论宽度,KZ也越接近1,引入的谐波电压也越小。
在对微流控芯片信号进行小波去噪时,应根据微流控芯片信号的特点,选取合适的小波基函数,以确保对信号的去噪效果。图2表示在信号去噪过程中,小波变换的分解层数均为4层,不同的小波基对模拟微流控芯片信号去噪处理后信号的均方根误差和信噪比的结果曲线。图中,横坐标表示小波基,其中1~9表示小波基db1~db9;2~18表示小波基sym1~sym9;19~32表示小波基bior1.1~bior6.8;33~38表示小波基coif1~coif5。
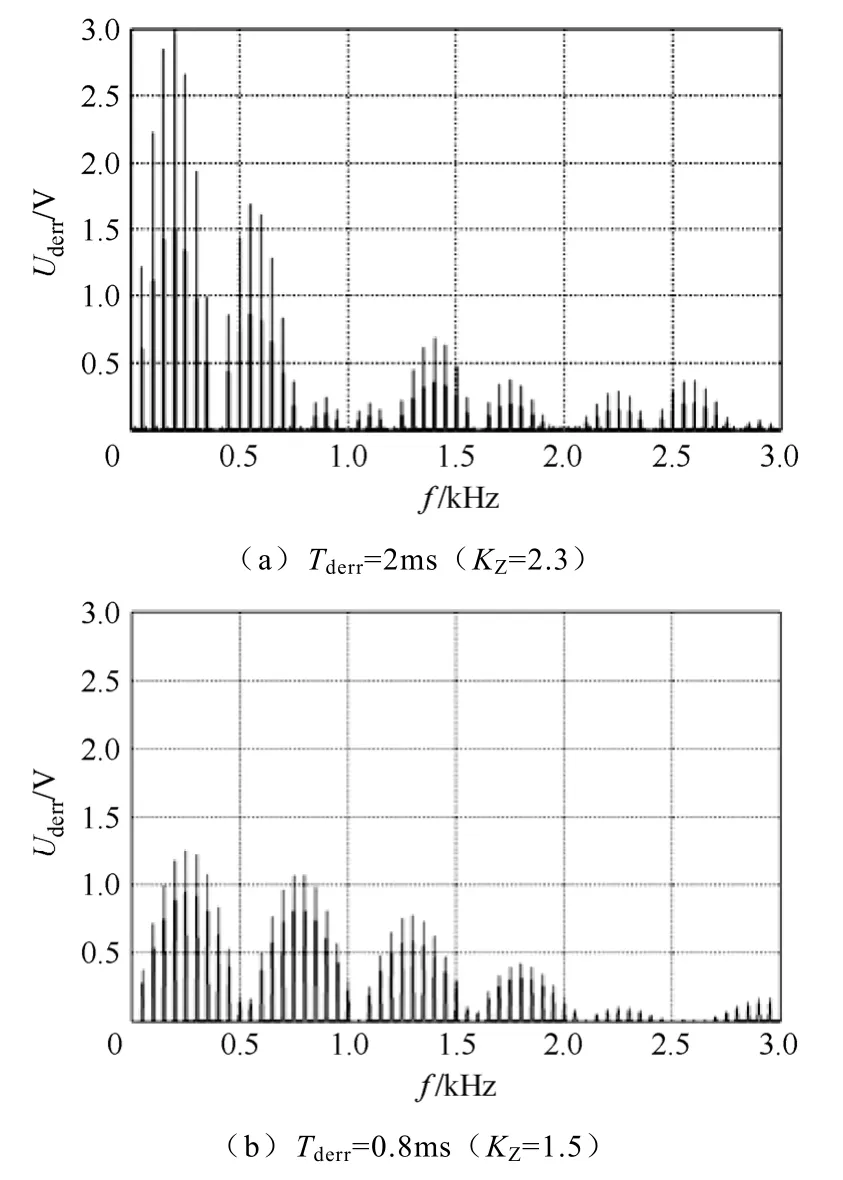
图5 死区电压Uderr的频谱分析图Fig.5 Harmonic contents of dead-time voltage Uderr
4 在线自适应方法
如上分析可知,采用上述的死区消除方法,只要能够精确确定电感电流的过零理论宽度Tth,使加入死区的检测过零宽度Tft尽量接近该理论宽度Tth,就基本能在整个正弦调制周期内完全消除死区效应,从而极大地减小基波电压损失和低次谐波含量,改善输出正弦波质量。但在逆变器应用中,负载阻抗的情况变化多样,不同的负载阻抗角会使电流过零点位置产生较大变化,一方面导致过零理论宽度Tth发生动态变化,另一方面给过零检测宽度Tft的测量带来更大的困难,因此,必须动态地跟踪负载变化,自适应地计算不同负载下的过零理论宽度,设计最为合理的过零检测宽度在线算法,并减小算法对于检测器件特性的依赖度,才能够实现最优的死区消除效果,使该死区消除方法具有工程实用意义。
图6是逆变器中电压电流波形的关系示意图,其中图6b是图6a在电流iL过零区域的细节放大图。如图所示,iL是电感电流,uout是输出电压,uch1是逆变器桥臂侧输出电压uc的基波分量。设uout超前iL的阻抗角为φ1,uch1超前iL的阻抗角为φ2。显然,在电感电流iL过零处,一个开关周期内iL的变化量Δi如下所示:
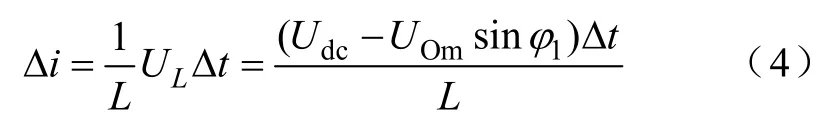
式中L——逆变器输出滤波电感;
Udc——直流母线电压;UOm——输出电压幅值。
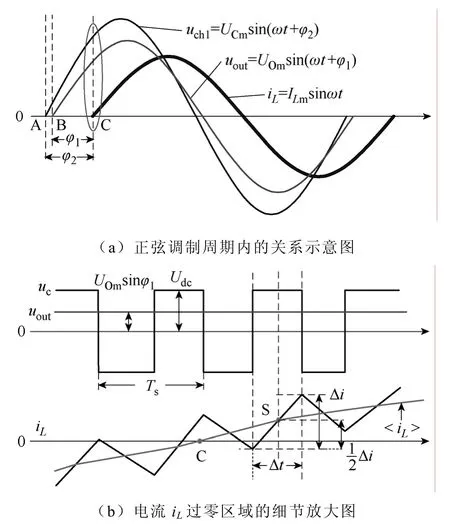
图6 逆变器中电压电流波形关系示意图Fig.6 Relationship between the voltage and current waveforms
又根据正弦波PWM调制原理可知
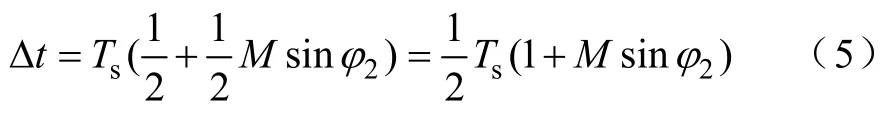
式中Ts——开关周期;
M——逆变器调制比。
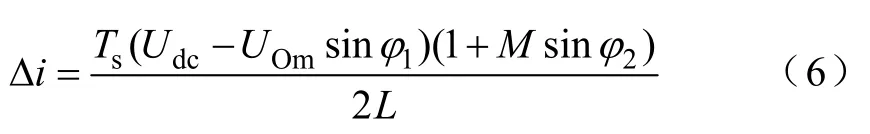
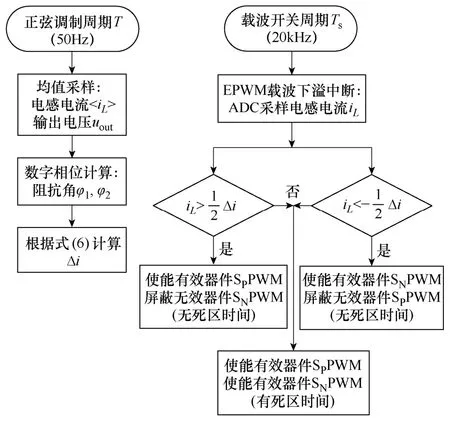
图7 在线自适应算法程序流程图Fig.7 Program flowchart of the online adaptive algorithm
5 仿真验证
为了验证本文提出的在线自适应死区消除方法,采用PSIM仿真软件搭建单相全桥逆变电路和相应控制模型。逆变器采用双极性SPWM调制,参数设定为:输出功率为1kVA,输出滤波电感L为4mH,滤波电容C为1μF,直流母线电压Udc为400V,输出电压Uout为AC 220V,输出电压基波频率f为50Hz,PWM开关频率fs为20kHz。
图8表示纯阻负载下,死区时间Td=4μs时的输出电压和电感电流波形。其中图8a是采用本文提出的在线自适应算法得到的波形,其过零检测宽度近似等于过零理论宽度,即过零宽度系数KZ≈1。图8b和图8c是没有采用本文所示方法,并设过零检测宽度和过零理论宽度存在相对误差时得到的波形。其中图8b是KZ=1.5,即过零检测宽度大于过零理论宽度时的波形;图8c是KZ=0.5,即过零检测宽度小于过零理论宽度时的波形。下表中详细列出了各种工作条件下逆变器输出电压的THD情况。
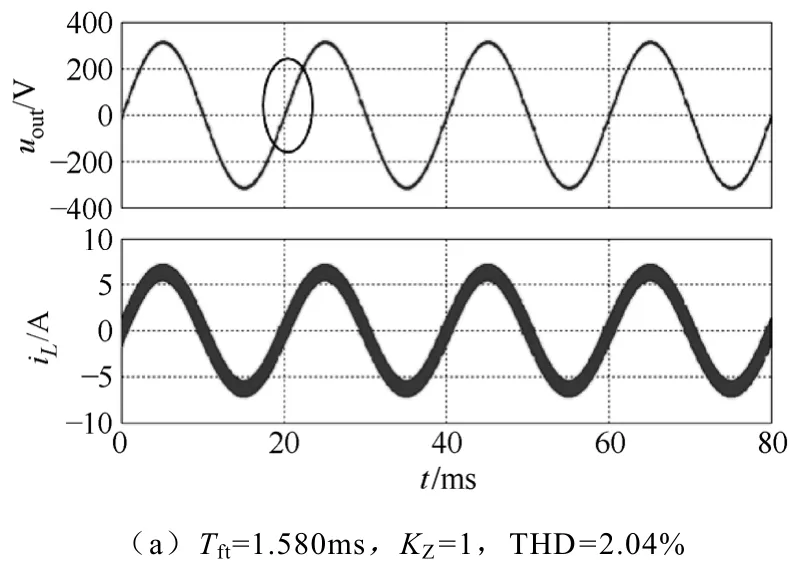
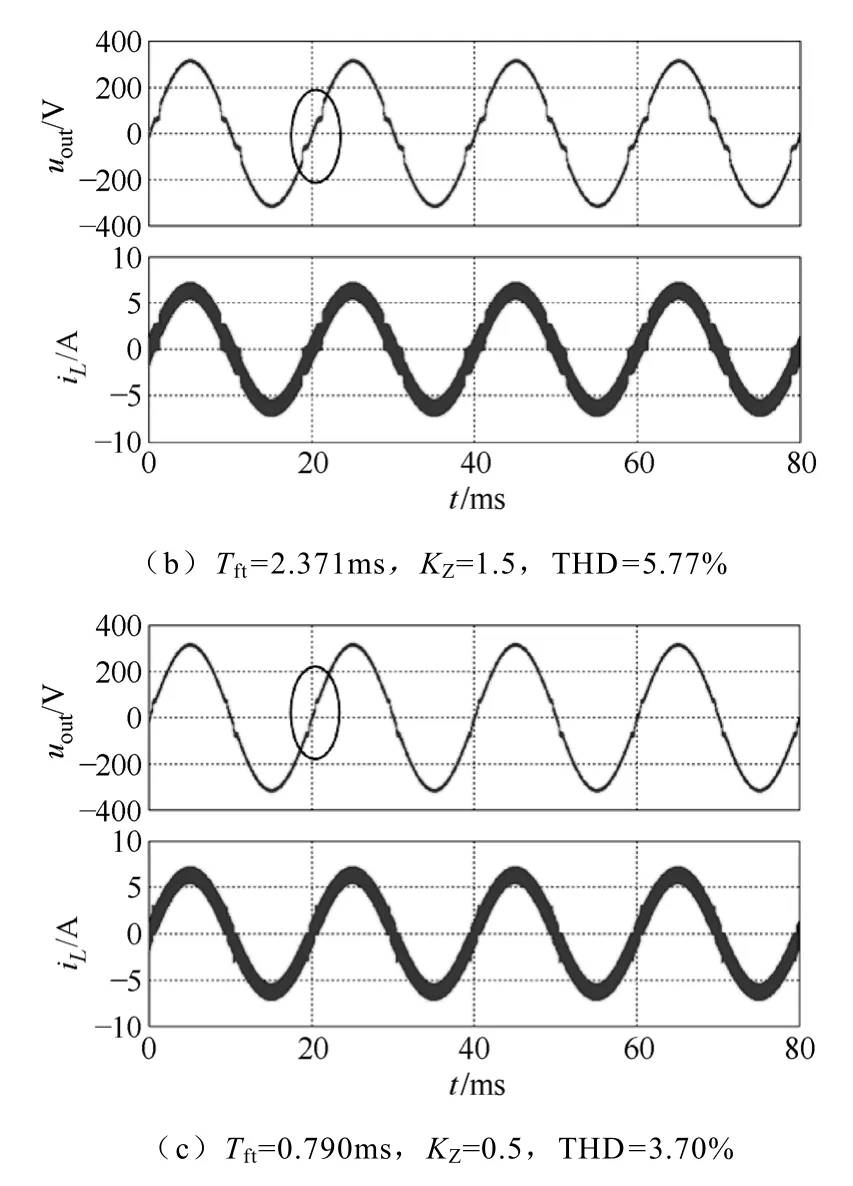
图8 φ1=0°, Td=4μs时的电压电流仿真波形Fig.8 Simulation waveforms of the output voltage and inductive current at φ1=0°,Td=4μs
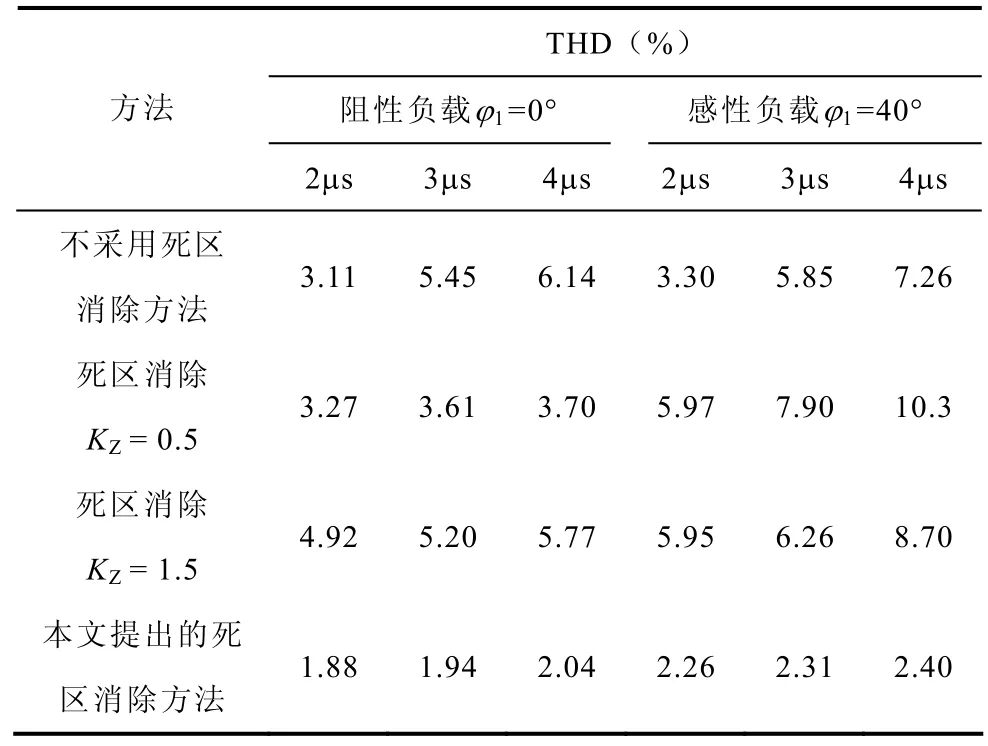
表 输出电压THD比较Tab.Comparison of output voltage THD
从仿真结果可以清楚地看到,无论过零检测宽度大于还是小于过零理论宽度,电压波形在电流过零处都会出现明显畸变,低次谐波含量增加,THD增大,另外由于在电流非过零区域消除了死区,基波电压的跌落相应减小;而本文提出的在线自适应死区消除方法,除了能避免输出电压基波损失外,在改善输出波形方面,对负载阻抗情况和死区时间大小均不敏感,无论对阻性负载还是感性负载,无论死区时间长短,都能明显改善电压波形在电流过零处的畸变,使电压THD显著减小。
6 实验结果
最后,设计一台单相逆变器来进一步验证上述理论分析和仿真结果的正确性。系统电路具体参数如下:直流母线电压Udc=390V,输出电压基波频率f=50Hz,PWM开关频率fs=20kHz,调制比M=0.8;输出滤波电感L=3.8mH,滤波电容C=1μF;采用三菱公司的IGBT-IPM PS21867搭建功率开关电路,采用国产电流霍尔TBC50AP采样电感电流,采用Ti公司的DSP芯片TMS320F2808实现本文提出的在线自适应死区消除方法。
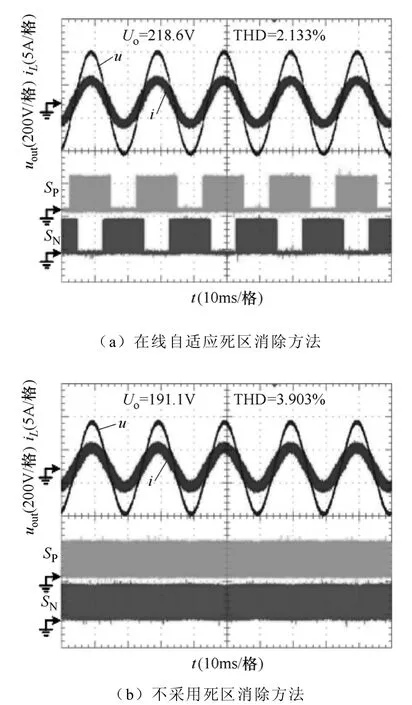
图9 阻性负载,Td=2μs时的实验波形Fig.9 Experimental results of resistive load at Td=2μs
图9 是阻性负载,输出功率为500W时,死区时间Td=2μs的实验波形。其中图9a是采用在线自适应死区消除方法的电压电流及门极驱动波形,输出电压有效值为218.6V,THD为2.133%。图9b是不采用死区消除方法的波形,由于死区效应,输出电压有效值降低为191.1V,THD增大为3.903%。图10是死区时间Td=4μs的实验波形。其中图10a是采用在线自适应死区消除方法的波形,输出电压有效值为217.8V,THD为2.164%;图10b是不采用死区消除方法的波形,输出电压有效值166.8V,THD为6.261%。
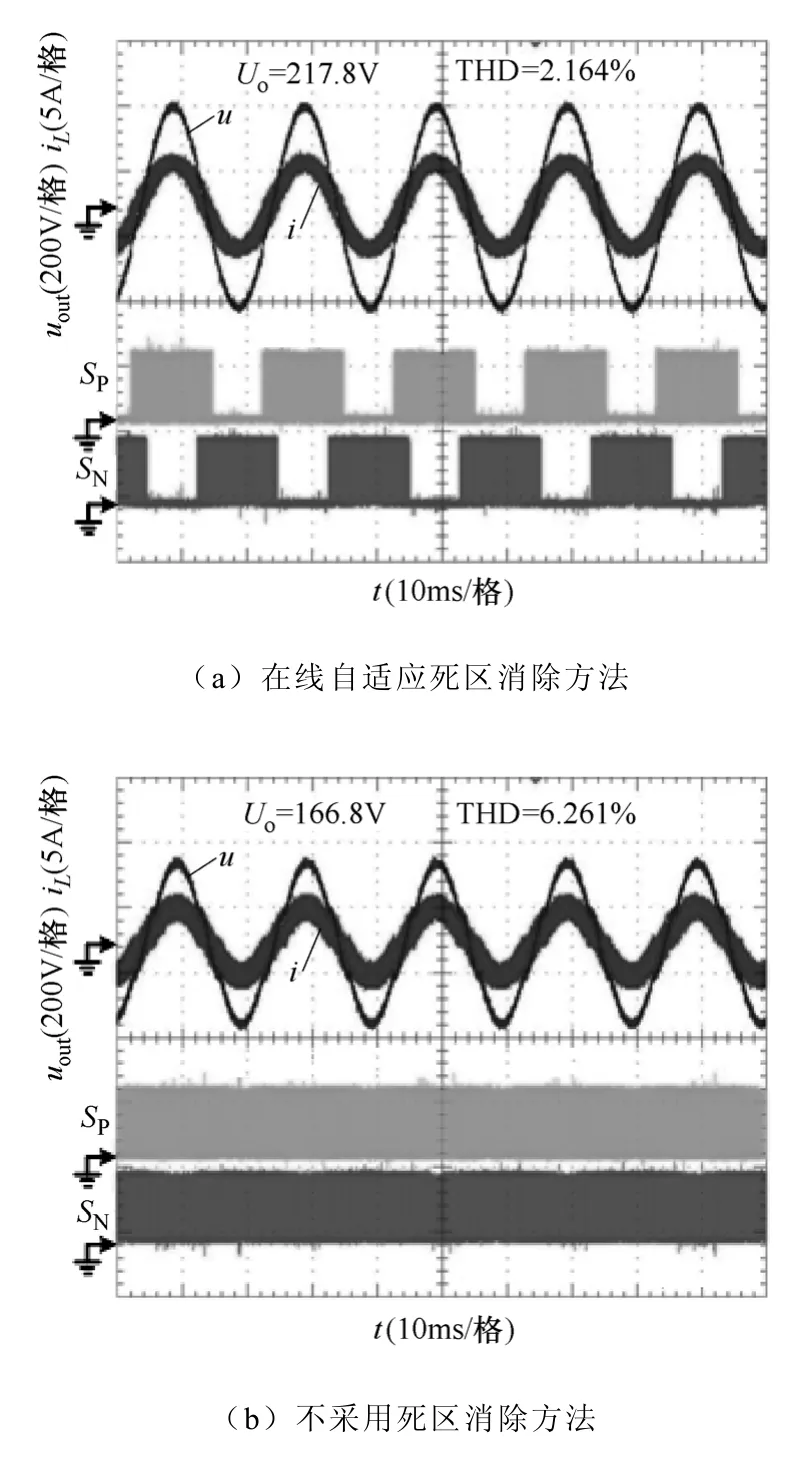
图10 阻性负载,Td=4μs时的实验波形Fig.10 Experimental results of resistive load at Td=4μs
图11 和图12是单相异步电动机负载,输出有功功率为330W时的实验波形。图11的死区时间Td=2μs,其中图11a是采用在线自适应死区消除方法后的波形,输出电压有效值为207.2V,THD为2.281%;图11b是不采用死区消除方法的波形,输出电压有效值为192.8V,THD为3.215%。图12的死区时间Td=3.5μs,其中图12a是采用在线自适应死区消除方法后的波形,输出电压有效值为199.4V,THD为2.527%;图12b是不采用死区消除方法的波形,输出电压有效值为171.4V,THD为5.857%。
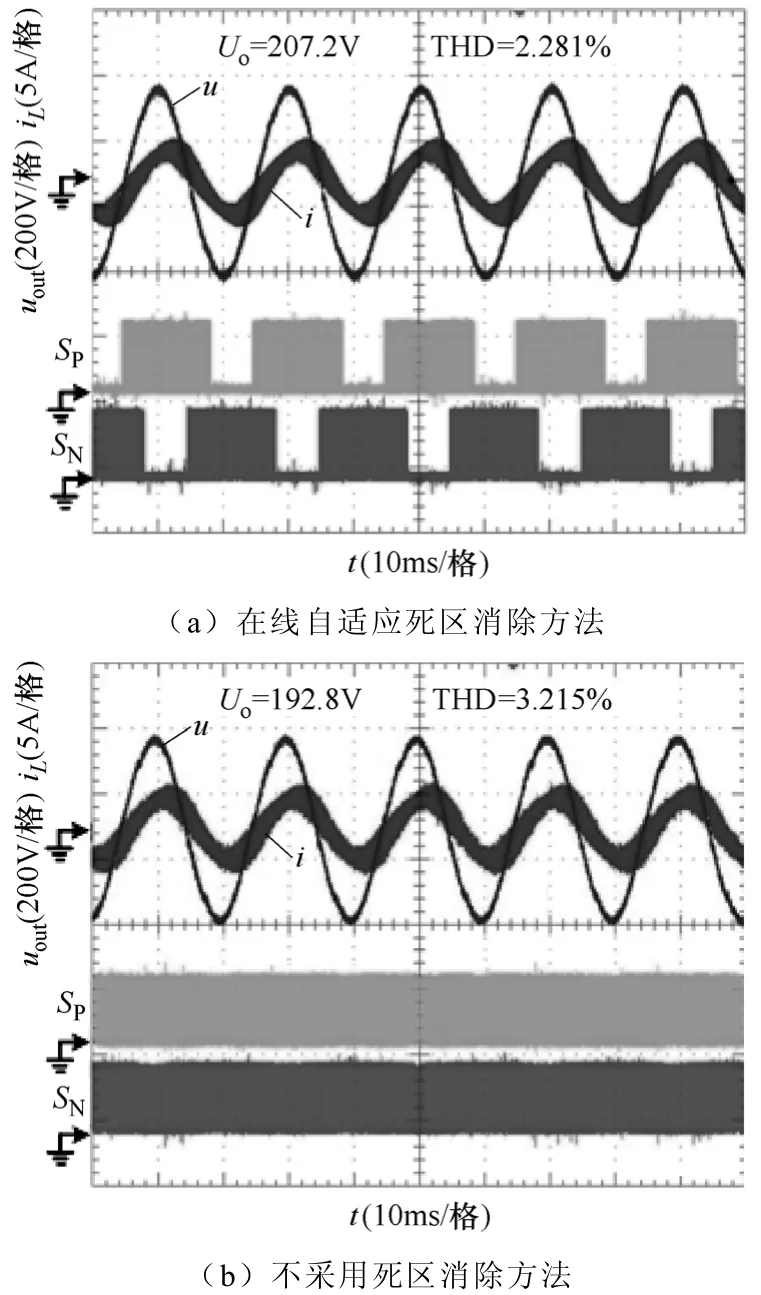
图11 感性负载,Td=2μs时的实验波形Fig.11 Experimental results of inductive load at Td=2μs
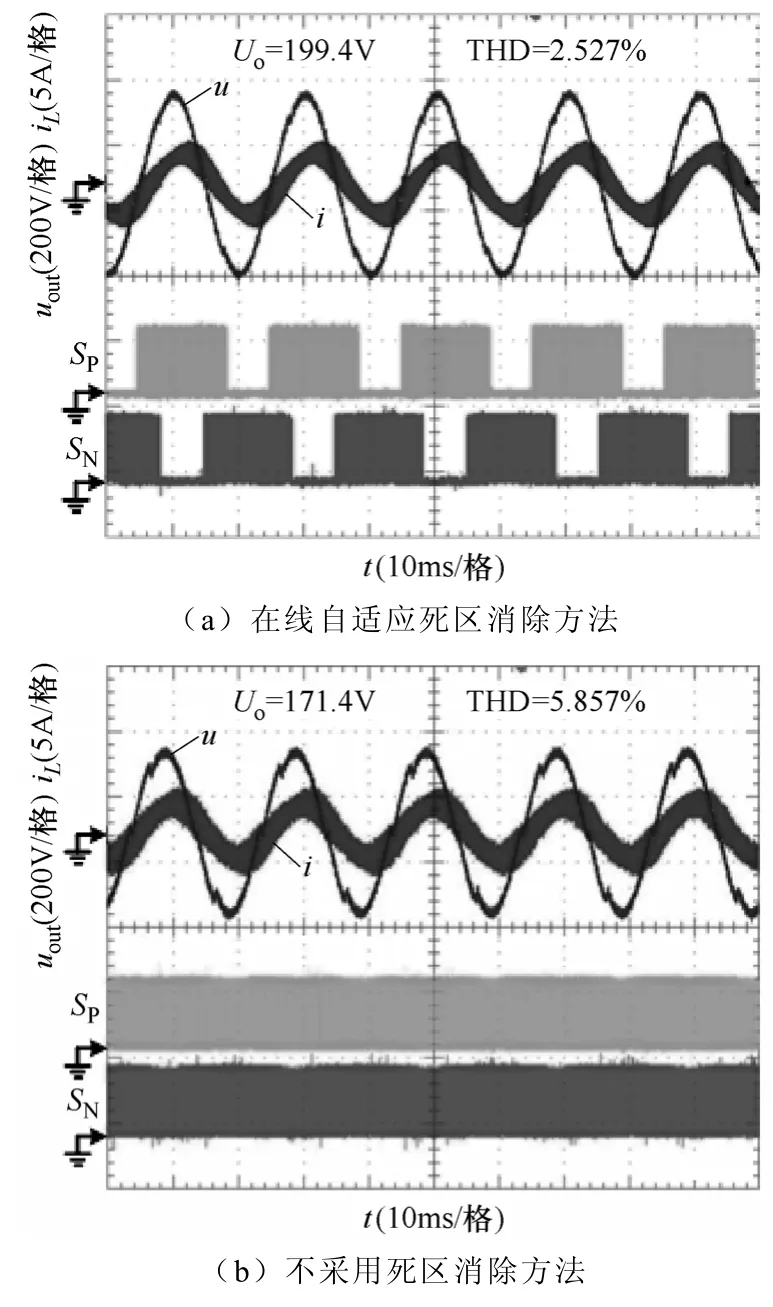
图12 感性负载,Td=3.5μs时的实验波形Fig.12 Experimental results of inductive load at Td=3.5μs
实验波形和结果表明:一方面,本文提出的在线自适应死区消除方法不会改变有效开关器件的占空比分布,因此不会影响逆变器输出的动态性能。另一方面,该死区消除方法不依赖高精度的电流采样器件,并且无论对阻性负载还是感性负载,无论死区时间大小,都能有效消除死区效应,降低基波电压损失,明显减小低次谐波含量和电压THD,对电流过零处的电压畸变抑制效果尤为明显,较大地改善了输出正弦波形质量。
7 结论
本文提出一种在线自适应的PWM死区消除方法,该方法将死区效应分为电流过零区域和电流非过零区域两部分。通过在线跟踪负载变化,自适应地计算出不同负载下最优的电流过零理论宽度,从而精确实现电流过零区域和电流非过零区域死区效应的分别消除,以达到最佳的死区消除效果,使逆变器在各种负载情况下输出高质量的正弦波。仿真和实验结果均证明,该方法能有效消除死区效应,减小输出电压基波损失和低次谐波含量,特别对电流过零点处电压畸变的抑制效果明显,使输出电压THD显著减小。
[1] Jeong S G,Park M H.The analysis and compensation of dead-time effects in PWM inverters[J].IEEE Transactions on Industry Electronics,1991,38(4):108-114.
[2] Wu C M,Lau W H,Chung H S.Analytical technique for calculating the output harmonics of an H-bridge inverter with dead time[J].IEEE Transactions on Circuits and Systems-I: Fundamental Theory and Applications,1999,46(5): 617-622.
[3] 刘军锋,李叶松.死区对电压型逆变器输出误差的影响及其补偿[J].电工技术学报,2007,22(5): 117-122.Liu Junfeng ,Li Yesong.Dead-time influence on output error of voltage source inverter and compensation[J].Transactions of China Electrotechnical Society,2007,22(5): 117-122.
[4] Munoz A R,Lipo T A.On-line dead-time compensation technique for open-loop PWM-VSI drives[J].IEEE Transactions on Power Electronics,1999,14(4): 683-689.
[5] Drevensek D,Curkovic M,Jezernik K.Dead time influence compensation considering switching times of power transistors[C].Proceedings of the Power Electronics and Motion Control Conferonce,1996:611-616.
[6] Takashi Sugegawa,Kenzo Kamiyama,Katsuhiro Mizuno,et al.Fully digital vector-controlled PWM VSI-fed ac drives with an inverter dead-time compensation strategy[J].IEEE Transactions on Industry Applications,1991,27(3): 552-559.
[7] Attaianese C,Tomasso G.Predictive compensation of dead time effects in VSI feeding induction motors[J].IEEE Transactions on Industry Applications,2001,37(3): 856-863.
[8] Urasaki N,Senjyu T,Uezato K,et al.An adaptive dead-time compensation strategy for voltage source inverter fed motor drives[J].IEEE Transactions on Power Electronics,2005,20(5): 1150-1160.
[9] Hyun-Soo Kim,Hyung-Tae Moon,Myung-Joong Youn.On-line dead-time compensation method using disturbance observer[J].IEEE Transactions on Power Electronics,2003,18(6): 1336-1345.
[10] Attaianese C,Nardi V,Tomasso G.A novel SVM strategy for VSI dead-time-effect reduction[J].IEEE Transactions on Industry Applications,2005,41(6):1667-1674.
[11] 何正义,季学武,瞿文龙.一种新颖的基于死区时间在线调整的SVPWM补偿算法[J].电工技术学报,2009,24(6):42-47.He Z Y,Ji X W,Qu W L.A novel SVPWM compensation strategy based on regulating dead time on-line[J].Transactions of China Electrotechnical Society,2009,24(6): 42-47.
[12] Shihong Park,Jahns T M.A novel dead-time elimination method using single-input enhanced phase-leg configuration[C].Proceedings of the IEEE Industry Applications Conference Annual Meeting,Salt Lake City,USA,2003,3: 2033-2040.
[13] Zhang B,Huang A Q,Chen B.A novel IGBT gate driver to eliminate the dead-time effect[C].Proceedings of the IEEE Industry Applications Conference Annual Meeting,Hong Kong,China,2005,2: 913-917.
[14] Choi Jung Soo,Yoo Ji Yong,Lim Seung Won,et al.A novel dead time minimization algorithm of the PWM inverter[C].Proceedings of the IEEE Industry Applications Conference Annual Meeting,Phoenix,USA,1999,4: 2188-2193.
[15] Chen L H,Peng F Z.Dead-time elimination for voltage source inverters[J].IEEE Transactions on Power Electronics,2008,23(2): 574-580.

