移相控制对称半桥变换器软开关条件

蒋 玮 胡仁杰 黄慧春

（东南大学电气工程学院 南京 210096）

1 引言

双向DC-DC变换器因其在新能源、分布式发电系统、电动汽车等领域良好的应用前景，得到了越来越多的关注。作为连接两个不同电压等级的中间环节，双向DC-DC变换器可以方便的进行能量的调节和管理。移相控制对称半桥变换器[1,3]，作为一种新型双向DC-DC变换器，它在同样电压等级下，器件数量比全桥变换器减少一半，在两个工作方向上都可以不使用附加电路实现零电压开关，并可通过附加电路实现零电流开关[5]，且因为输入端加入了升压电感，其升压比更高，控制更灵活。

文献[1-2]对移相控制对称半桥变换器的工作原理进行了描述。文献[3]给出了移相控制对称半桥变换器实现零电压开关所需的升压电感、变压器漏感和滤波电感的选择依据，但是未对谐振过程进行分析。

在实际设计过程中，移相控制对称半桥变换器输入端升压电感、变压器漏感和滤波电感往往是根据对纹波和功率的要求而选定的，无法完全以满足软开关条件作为设计依据。较为实用的设计应该是在电感值确定后，分析其和寄生电容的谐振过程是否能满足软开关要求，如果不能满足，则可以通过外并电容或串接小电感的方式，对谐振电路的特征阻抗进行微调，但是这就要求有可供分析的谐振参数条件关系。目前对于软开关条件的研究，多是从谐振器件能量角度[11,19]，或是针对辅助电路设计进行分析[12-13]，且多见于全桥移相变换器[7-9]。本文在分析移相控制对称半桥变换器工作过程的基础上，原创性地通过对一、二次开关过程中的等效电路进行分析，指出了电路寄生参数对软开关过程的影响，推导出满足零电压开关条件的谐振参数取值条件，可作为变换器设计的参考。并以此为依据，设计了一500W的实验样机，实验结果证明了根据该条件设计出的变换器可以在设计功率等级上完成软开关，减小开关损耗并提高变换器的工作效率。

2 变换器工作原理

移相控制对称半桥变换器如图1所示，高压变压器T左侧为低压侧Vl，右侧为高压侧Vh。低压侧输入端有一个大电感Li，起到平波和存储能量的作用，输入电流为il。功率开关器件Q1和Q2以互补的方式交替导通，Q3和Q4以互补的方式交替导通，两个半桥导通角之间有一个相位差φ1，在变压器漏感Ls两端形成两个方波电压vp和vs。通过调节φ1的超前与滞后，以及φ1的大小，就可以决定能量是由低压侧流向高压侧（正向工作），还是从高压侧流向低压侧（反向工作），这就是移相控制方式。变压器T起到隔离和电压匹配的作用，变压器漏感Ls在两个半桥之间通过漏感电流ip（一次）及is（二次）传递能量。C1～C4是分压电容，在足够大的情况下，可以认为其电压V1～V4不变。开关器件Q1～Q4均反向并联二极管VD1～VD4，Cr1～Cr4是开关器件的结电容，当结电容和变压器漏感发生谐振时，结电容放电至电压为零，此时开关器件反向并联二极管导通，从而为开关器件的零电压导通创造条件。

图1 移相控制对称半桥变换器Fig.1 Symmetry half-bridge converter with phase-shifted control

移相控制对称半桥变换器升压模式下共分为t0～t12的12个工作模态[2]，其开关时序及波形如图2所示，这12个模态的工作过程如下。

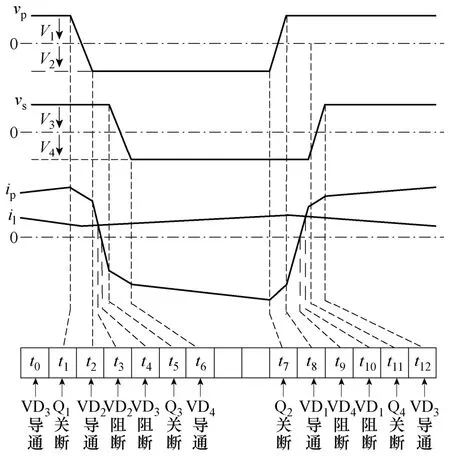
图2 Boost模式下开关时刻及电压电流波形Fig.2 Theoretical switch points and voltage and current waveforms under boost mode

模态1 (t0～t1)：电路达到稳态，Q1和VD3导通。

模态2 (t1～t2)：在t1时刻，Q1关断，Cr1、Cr2和Ls发生谐振，结电容Cr2电压vcr2从V1+V2开始下降，vp也开始从V1下降。

模态3 (t2～t3)：在t2时刻，vcr2由正变负，VD2因正偏而导通，从这段时间开始，Q2可以零电压开通。

模态4 (t3～t4)：从t3时刻起，变压器漏感电流ip开始小于输入电流il，所以Q2从VD2换流，在t4时刻，ip下降到0，VD3仍然导通。

模态5 (t4～t5)：ip由正变负，因此，电流从VD3向Q3换流，Q3零电压开通。

模态6 (t5～t6)：在t5时刻，Q3关闭，Cr3、Cr4和Ls发生谐振，分别开始充电和放电。

模态7 (t6～t7)：在t6时刻，结电容Cr4电压vcr4由正变负，VD4因正偏而导通，从这段时间开始，Q4可以零电压开通。

模态8 (t7～t8)：在t7时刻，Q2关闭，Cr1、Cr2和Ls再次发生谐振，这时结电容Cr1电压vcr1从V1+V2开始下降，vp从-V2开始上升。

模态9 (t8～t9)：在t8时刻，vcr1由正变负，VD1因正偏而导通，ip继续上升直到在t9时刻等于0，从这段时间开始，Q1可以零电压开通。

模态10 (t9～t10)：ip从t9时刻开始由负变正并继续上升，因此，电流从VD4向Q4换流，Q4零电压开通。

模态11 (t10～t11)：ip开始大于il，Q1零电压开通。

模态12 (t11～t12)：在t11时刻，Q4关断，Cr4、Cr3和分别开始充电和放电。在t12时刻，结电容Cr3电压vcr3由正变负，VD3因正偏而导通，至此，一个完整的工作周期结束。

3 软开关实现条件

通过变换器工作过程可知，移相控制对称半桥变换器实现零电压开关（Zero Voltage Switching,ZVS）的关键，是在开关器件关断过程中，开关器件并联电容与变压器漏感Ls发生谐振，并在对应桥臂开通之前，其并联电容电压下降至0，使反向并联二极管导通。因此，通过分析谐振过程，就可以推导出移相控制对称半桥变换器的软开关条件。

Boost模式下发生谐振过程的工作模态分别是模态2、模态5、模态8和模态12，其中模态2中的t1时刻Q1关断，继而Q2零电压开通；模态5中的t5时刻Q3关断，继而Q4零电压开通；模态8中的t7时刻Q2关断，继而Q1零电压开通；模态12中的t11时刻Q4关断，继而Q3零电压开通，这四个模态的等效电路如图3所示。

图3 发生谐振过程的工作模态Fig.3 Equivalent circuits when quasi resonances happen

下面以t1和t5时刻为例，分析一二次零电压开通所需的谐振器件条件，t7和t12时刻的条件与之类似。假设：①升压电感Li足够大，其上电流纹波很小，可将输入看成一个恒流源Ii；②变压器两侧的均压电容C1～C4足够大，使其上的电压V1～V4保持恒定，可以将其看做恒压源。

t1和t5时刻变换器的等效电路如图4所示，Cr1～Cr4为Q1～Q4的寄生电容，i1～i4为Cr1～Cr4上通过的电流，vcr1～vcr4为Cr1～Cr4上的电压，ip为变压器漏感电流，Ls为变压器等效漏感，Ls以及V3、V4都折算到变压器一次侧。

图4 t1和t5时刻等效电路图Fig.4 Equivalent circuits at t1 and t5

因为开关器件参数的对称性，设Cr1=Cr2=Cr，由图4的等效电路可以分别获得t1和t5时刻的状态方程：

由式（1）、式（2）可获得相应的二阶微分方程，分别代入t1和t5时刻的初始条件ip(t1)、ip(t5)、vcr2(t1)和vcr4(t5)，可以获得模态2和模态6过程中开关器件寄生电容vcr2和vcr4的表达式：

由式（3）可以分析在模态2中谐振电容电压vcr2随时间的变化关系。我们容易看出，在ωr(t-t1)=π/2时刻，vcr2达到最小值vcr2min=V2+V3-Zr(Ip-Ii)，因此，Q2能够实现ZVS的关键，就是在该模态结束前，vcr2能够下降到0，从而使二极管VD2导通，

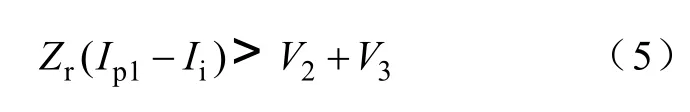
在一定的输出功率下，Ip1、Ii、V2、V3都可以通过稳态条件获得[2]，只要选择合适的外接电容和电感参数，使得

同理，在模态4中，由式（4）可得Q4零电压开通的条件，是在时，vcr4＜0，即特征阻抗值满足以下条件：

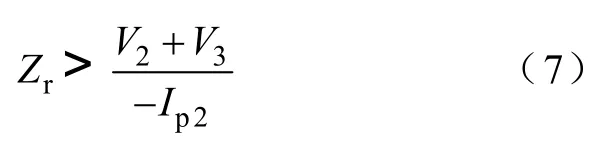
从式（6）、式（7）可以看出，在变压器漏感Ls一定的情况下，开关器件寄生电容较小，可以加快谐振过程，使并联电容在谐振模态结束前其两端电压下降至0，为开关器件提供ZVS条件。但是，开关器件并联电容的也不能过小，还是以t1时刻为例，在谐振完成后，Q2的反并二极管VD2导通，此时有

rcr1早下降到0，ip开始下降，当ip下降到ip＜Ii时，Q2还没有开通，则Cr1将重新开始充电，Q2端电压将大于0，失去ZVS的条件。而谐振是在死区Q1和Q2开关信号之间的死区时间完成的，因此为了避免这种情况的发生，一般来说，可以通过在开关器件上并联满足式（6）、式（7）确定的特征阻抗要求的容值上限1/2左右的电容帮助谐振。

同时控制系统设计时还应考虑死区时间Td，使其既能使满足vcr2、vcr4达到最小值需要的时间，又不至于过大使寄生电容重新开始充电，一般来说，取为谐振周期。

4 实验结果

为了验证上述谐振器件选择条件的有效性，设计了500W移相控制对称半桥变换器样机，图5所示的是样机的系统结构。系统采用电压电流双环控制，所产生的电压控制信号经相位调制转换为移相角，占空比D恒定。样机各项参数如下：

表 变换器样机参数Tab.Parameters of the prototype

图5 系统结构图Fig.5 Structure of the system

Q1、Q2选用了MOSFET FQA160N08，Q3、Q4选用了MOSFET IRFP460，其输入电容值均为5nF左右，电容值过小。因此选取了2组电容并联在开关器件上，第一组为20nF，第二组为100nF，第二组电容值超过了并联谐振电容值的上限，不满足软开关要求。

使用Rigol品牌的DS1000E型号数字示波器采集实验波形，图6为变压器漏感电流波形，图7为Q1、Q3驱动信号波形。两组的Q2端电压和Q2门极信号波形如图8所示，其中CH1显示的是Q2的门极信号vg2，CH2是Q2的漏源极电压vce2。

图6 变压器漏感电流波形Fig.6 Current waveform of the transformer’s leak inductor

图7 Q1、Q3驱动信号波形Fig.7 Drive signal of Q1 and Q3

图8 不同谐振参数下的Q2实验波形Fig.8 Experimental waveforms of Q2 with different resonance elements’ parameters

如图8a所示，vce2在门极信号到来之前已经下降到0，而图8b中，因谐振电容过大，vce2到0之前，门极信号已经到来。通过该实验结果可以看出，以本文推导的条件为依据，选择不同的开关器件并联电容参数，可以改变谐振过程，实现开关器件反向并联二极管的导通，从而实现开关器件的零电压开通。

5 结论

本文简要介绍了移相控制对称半桥变换器的工作原理，指出了其开关元件软开关的实现是依靠变压器漏感和开关元件并联电容发生的准谐振过程。分析了准谐振过程中不同状态的变换器等效电路，并推导出了实现软开关所需的变换器开关元件及变压器寄生参数应满足的条件，以及对死区时间的要求。以这些条件为依据，选取了相关参数，进行了变换器样机设计并完成了相关实验。实验结果证明移相控制对称半桥变换器无需附加元件即可以通过准谐振实现开关元件的软开关，本文推导出的结论可以作为选取参与准谐振器件参数的依据，简化变换器的设计过程。

[1] Peng Z,Hui L,GuiJia S,et al.A new ZVS bidirectional DC-DC converter for fuel cell and battery application[J].IEEE Transactions on Power Electronics,2004,19(1): 54-65.

[2] 马学军.数字移相控制隔离型半桥双向DC-DC变换器研究[D].武汉: 华中科技大学,2005.

[4] Xiao Huafeng,Xie Shaojun.A ZVS bidirectional DC-DC converter with phase-shift plus PWM control scheme[J].IEEE Transactions on Power Electronics,2008,32(2): 813-823.

[5] Bhajana,V,Reddy R.A novel ZVS-ZCS bidirectional DC-DC converter for fuel cell and battery application[C].Proceedings of the IEEE Power Electronics Specialist Conference,2009: 12-17.

[6] Lenke U,Hu Jiefang,De Doncker W.Unified steady-state description of phase-shift-controlled ZVS-operated series-resonant and non-resonant single-active-bridge converters[C].Proceedings of the IEEE Energy Conversion Congress and Exposition,2009: 796-803.

[7] Han S,Shin Y,ChangSeop K.A pulse frequency modulated full bridge DC-DC converter with series boost capacitor[J].IEEE Transactions on Industrial Electronics,2011,99(3): 1～8.

[8] Kim E,Kwon B.Zero-voltage and zero-current switching full-bridge converter with secondary resonance[J].IEEE Transactions on Industrial Electronics,2010,57(3): 1017-1025.

[9] Liu F,Yan J,Ruan X.Zero-voltage and zerocurrent-switching PWM combined three-level DC-DC converter[J].IEEE Transactions on Industrial Electronics,2010,57(5): 1644-1654.

[10] Qiao Chongming,Keyue S.An isolated full bridge boost converter with active soft switching[C].Proceedings of the IEEE Power Electronics Specialist Conference,2004: 896-903.

[11] 胡红林,李春华,邵波.移相全桥零电压PWM软开关电路的研究[J].电力电子技术,2009,43(1): 12-14.Hu Honglin,Li Chunhua,Shao Bo.Reseach on phase shifted full-bridge ZVS converter[J].Power Electronics,2009,43(1): 12-14.

[12] 陈仲,张鑫,季飚,等.一种基于变压器串联和新型辅助网络的ZVS移相全桥变换器[J].电工技术学报,2009,24(12): 95-100.Chen Zhong,Zhang Xin,Ji Biao,et al.A ZVS phase-shifted full-bridge converter with seriesconnection of transformer and auxiliary network[J].Transactions of China Electrotechnical Society,2009,24(12): 95-100.

[13] 袁进行,马瑞卿,樊平.带辅助谐振的移相全桥ZVS DC-DC变换器研究[J].电力电子技术,2008,42(5): 23-25.Yuan jinxing,Ma Ruiqing,Fan Ping.Research on phase-shifted full-bridge ZVS DC-DC converter with auxiliary branch[J].Power Electronics,2008,42(5):23-25.

[14] Jeon SeongJeub,Cho GyuHyeong.A zero-voltage and zero-current switching full bridge DC-DC converter with transformer isolation[J].IEEE Transactions on Power Electronics,2001,16(5): 573-580.

[15] Khairy F,Lee Hyun Woo,Tomokaze M,et al.Boost-half bridge single power stage PWM DC-DC converter for small scale fuel cell stack[C].Proceedings of the IEEE International Conference on Power and Energy,2006: 426-431.

[16] Mao Hong,AbuQahouq J,Luo Shiguo,et al.Zerovoltage-switching half-bridge DC-DC converter with modified PWM control method[J].IEEE Transactions on Power Electronics,2004,19(4): 947-958.

[17] Chung H,Cheung Wai Leung,Tang S.A ZCS bidirectional flyback DC-DC converter[J].IEEE Transactions on Power Electronics,2004,19(11):1426-1434.

[18] 徐德鸿,马皓,汪槱生.电力电子技术[M].北京:科学出版社,2006.

[19] 姜雪松.隔离升压全桥 DC-DC 变换器拓扑理论和控制技术研究[D].北京: 中科院电工所,2006.