最小叉熵方法推导期权定价二叉树模型

李 英 华， 李 兴 斯

（1.大连理工大学 数学科学学院，辽宁 大连 116024；2.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024）

0 引 言

二叉树期权定价方法[1]（CRR）一直以其理论基础简单直观、操作简便而著称，因而成为期权定价数值方法的一个重要分支.随着金融市场以及期权的不断发展变化，二叉树方法也在相应地调整改善，以便更好地解决期权定价问题.

Jarrow等[2]为了能更有效地恢复风险中性概率，依据均值和方差条件，假定p＝1/2，可以得出参数p风险中性概率，其中u为标的资产价格上升的幅度，d为标的资产价格下降幅度，σ为股票价格波动率，则参数公式（JR）为

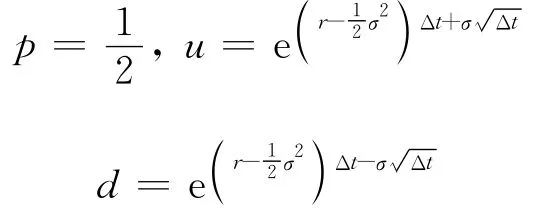
Trigeorgis[3]为了克服二叉树短步长的选取问题提出了二叉树参数公式（TGR），在已知资产价格分布的均值和方差的情况下，假设ud＝1，可得

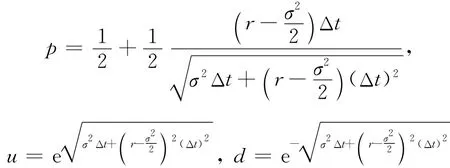
为了使参数p有限收敛，Wilmott[4]在1998年提出了两个二叉树参数模型（Wil1、Wil2），一个约定ud＝1，另一个约定p＝1/2；2001年Jabbour等[5]对标的资产服从离散或连续的布朗运动问题，针对不同漂移率，构造新的二叉树模型，若其模型变形，可以包容以前的几类二叉树期权定价模型，但是他们除了依据标的资产价格分布的均值方差以外，依然借助了p＝1/2或ud＝1或ud＝e2rΔt的条件；而文献[6～8]从二叉树模型的收敛性出发，依据标的资产分布的矩信息来构造二叉树参数公式，其中Benjamin等[7]就限定了期权敲定价K＝S0ujdn－j落在二叉树的最后一层节点中，并且这个最后一层节点数是奇数.

从上面二叉树的发展历程可以看出，二叉树期权定价模型的参数p、u、d的求解至今为止，都要借助于假定的第三方条件，有的时候还会出现负概率p，而且没有利用标的资产价格的历史信息，对于不同的标的资产价格分布没有一个统一的二叉树模型.本文针对这些问题用最小叉熵求解二叉树参数，主要是借助股票价格历史信息的一个先验（已知）概率，把nΔt时间点末的股票价格看成一个资产市场，在股票价格分布的矩信息约束下，若想求得nΔt时间点末尽可能靠近先验概率的风险中性概率，可依据叉熵函数[9]极小化来求得.新模型求解参数p、u、d时寓意明确，并且不论股票价格遵循什么分布，都可以用该模型来求解，因此可以看成是一个统一的模型.

1 期权的二叉树模型参数[1]

本文S0表示股票的初始价格，S表示股票的当前价格，K为期权执行价格，μ为股票的预期收益率，σ为股票价格波动率，r为无风险利率，T为期权有效期.考虑在风险中性市场中，一个不支付红利股票期权估值问题，就要先计算参数p、u、d.

二叉树图就是指每一个树图节点在下一个时刻会有两种可能状态，即若现在股票价格为S，经过Δt时刻则分别以p或1－p的概率机会达到uS和dS（u＞1，0＜d＜1，d＜1＋r＜u）的价格状态.由于市场是风险中性的，则Δt时间点末股票价格的期望值为SerΔt，有

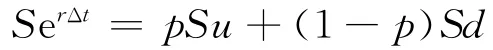
即

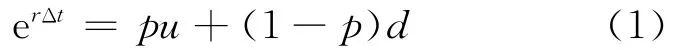
通常假定股票价格S遵循几何布朗运动，即其中ε为标准正态分布的随机数值，因此，在Δt时段内股票价格变化的方差为

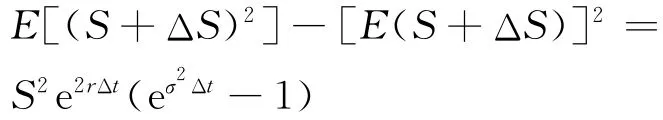
得

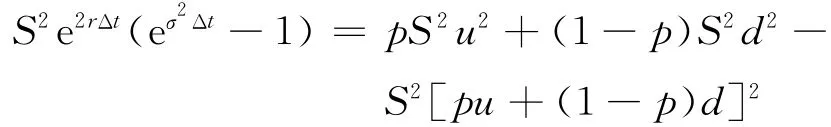
即

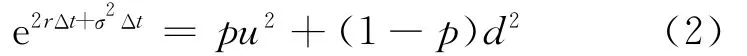
考虑计算需要，给定ud＝1，则联立方程（1）、（2）可得二叉树参数公式（CRR）：

黄河流域水质变化趋势总体变好的原因主要包括：新水法、水污染防治法颁布实施和国家节能减排政策的强力推行，“十一五”水资源保护和水污染防治规划的落实，流域排污总量持平及污染物浓度降低，以黄河水量统一调度为平台的水量水质保护并重，来水条件改善和水量调度优化而形成的河道环境容量增大。

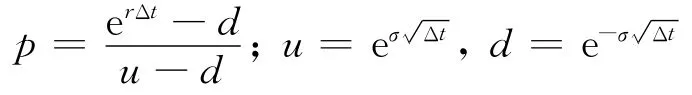
2 最小叉熵方法构造二叉树期权定价模型参数

在二叉树模型中，nΔt时刻末股票在一定概率分布下达到未来的价格状态，在信息不完全的情况下，存在先验概率，可以采用最小叉熵方法来求最靠近先验概率的概率分布，这是简洁实效的方法.它强调若想使待求的概率分布在服从已知信息（约束）的条件下，尽可能地靠近一个先验概率的概率分布，则必须令叉熵函数极小化.本文是在已知股票价格变化的历史信息下，依据股票价格变化的均值和方差来求二叉树模型的参数，所以目标函数为股票价格在某个时间点末的概率分布.最小叉熵方法构造二叉树期权定价模型的方法，即本文新方法的具体求解思路如下：

首先根据股票价格的历史数据来计算先验概率q.记Sh，h＝－1，－2，…，－H为S0前H时刻的股票价格，根据二叉树的变化规律有

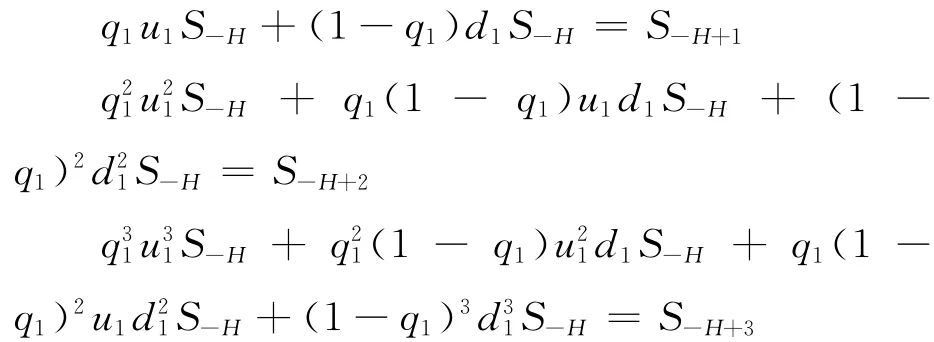
由上 面 的 式 子 可 以 得 出q1、u1、d1，然 后 计 算可以求得先验概率q.

其次，用最小叉熵方法求最靠近q的二叉树期权定价的参数，具体模型为

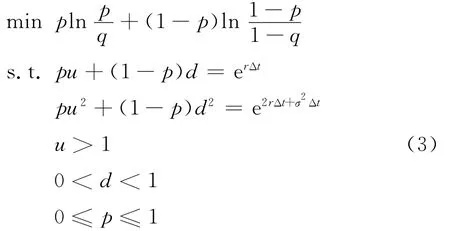
在式（3）中，未知变量是p、u、d，已知变量是r、σ、Δt、q，目标函数表示股票价格在未来某个时间点末最靠近先验概率的未来价格状态的概率分布；约束1和2为根据无套利和风险中性条件表示未来某个时间点股票价格变化描述的一、二阶矩约束的变化形式；约束3～5分别表示参数u、d、p在经济现象中的实际含义，故有相应的界限.

式（3）是非线性规划问题，用现有的非线性规划方法很容易求解，或者可以通过其对偶规划转化成无约束优化问题也比较好求.另外，由文献[10、11]知若叉熵函数最小化表达式约束条件（约束矩）不同，可以对应得出不同的概率分布，如正态分布、泊松分布等.因此，新模型（3）可以看成是一个对股票价格遵循多种随机运动形式的统一求解期权价格的模型.

显然由式（3）求出的参数p不会为负，并且p、u、d的求解具有明确的经济和物理含义，没有出现ud＝1或ud＝e2rΔt或p＝1/2等这样的强制条件.

在求得p、u、d之后，求解期权价格的方法同文献[1].通过式（3）可以求得不支付红利的欧式和美式期权的价格.对于支付红利或其他奇异期权的价格可以根据实际条件对式（1）～（3）进行相应的调整，亦可求出二叉树的参数值，进而可以确定期权的价格.

3 数值算例

算例1 考虑一个在有效期内不支付红利股票的欧式看涨期权的估值.假设S0＝100，K＝100，r＝0.05，σ＝0.3，期权有效期取T＝1 a.表1给出了取不同的时间步长Δt＝T/n（n＝1，5，10，20，30，50，75，100）时，本文新方法与 B－S、CRR、JR、TGR、Wil1、Wil2方法计算期权价格的结果.

表1 B－S、CRR、JR、TGR、Wil1、Wil2、本文新方法欧式看涨期权定价的比较Tab.1 The European call options pricing comparison by the models B－S，CRR，JR，TGR，Wil1，Wil2 and the new method in this paper

通过表1可以看出本文新方法不会出现二叉树参数为负的情况，而且其收敛速度不低于其他二叉树模型.其在奇（偶）步长n处，相对于其他模型收敛到B－S公式的速度更快，而且整体计算相对于其他二叉树模型更稳定.

4 结 论

本文依据股票价格历史信息得出先验概率，在此先验概率基础上用最小叉熵方法构造了二叉树期权定价方法中的参数p、u、d，有效地克服了参数p出现负值的情况，并且每个参数的确定都有明确的理论依据，数值算例表明新方法具有较快的收敛速度和较高的计算精度，相对于其他二叉树期权模型来说计算稳定，但对其在价内价外期权的定价性能及收敛性分析还有待于进一步研究讨论.

[1]COX J C，ROSS S A，RUBINSTEIN M.Option pricing：a simplified approach [J].Journal of Financial Economics，1979，7（3）：229－263

[2]JARROW R A，RUDD A.Option Pricing [M].Homewood：Irwin，1983

[3]TRIGEORGIS L. A log－transformed binomial numerical analysis method for valuing complex multioption investment [J].Journal of Financial and Quantitative Analysis，1991，26（3）：309－326

[4]WILMOTT P.Derivatives：the Theory and Practice of Financial Engineering [M].West Sussex：Wiley，1998

[5]JABBOUR G M，KRAMIN M V，YOUNG S D.Two－state option pricing：binomial models revisited[J].Journal of Futures Markets，2001，21（11）：987－1001

[6]DIENER F，DIENER M.Asymptotics of the price oscillations of a European call option in a tree model[J].Mathematical Finance，2004，14（2）：271－293

[7]BENJAMIN J，ANTONINO Z.A moments and strike matching binomial algorithm for pricing American put options[J].Decisions in Economics and Finance，2008，31（1）：33－49

[8]JOSHI M S.Achieving smooth asymptotics for the prices of European options in binomial trees [J].Quantitative Finance，2009，9（3），171－176

[9]KULLBACK S.Information Theory and Statistical Mechanics[M].New York：John Wiley ＆ Sons，1959

[10]REESOR R M，MCLEISH D L.Risk，entropy and the transformation of distributions [J]. North American Actuarial Journal，2003，7（2）：128－144

[11]LEHMANN E.Theory of Point Estimation [M].New York：John Wiley ＆Sons，1983