双指数效用函数组合投资决策
周 庆 健, 吕 思 瑶, 焦 佳, 赵 建, 魏 连 鑫, 闫 博
(1.大连理工大学 系统工程研究所,辽宁 大连 116024;2.大连民族学院 理学院,辽宁 大连 116600;3.同济大学 经济与管理学院,上海 200092;4.上海理工大学 理学院,上海 200093;5.大连海事大学 交通运输管理学院,辽宁 大连 116026)
0 引 言
在证券组合投资中,每位投资者都有自己对所获投资收益满足程度的效用函数,并利用期望效用最大化原则来选择最优组合,且大部分投资者是理性的风险厌恶型,他们在追求收益最大化的同时还希望降低风险.双指数效用函数U=c1+a1[2-exp(-a2(R-c2))-exp(-a3(R-c2))](R表示投资收益,其中ai>0,i=1,2,3)是一类典型且被投资者广泛应用的风险厌恶型效用函数,它在组合投资中具有非常重要的地位.
20世纪50年代初,美国金融学家Markowitz提出的投资组合理论可看成是这类问题的奠基石.该理论指出:投资者以提高投资收益同时减少投资风险为目标来确定最优组合.以此他建立了著名的均值-方差模型[1].
设有n种证券,当前(t=0)价格分别是S10,S20,…,Sn0,将来某任意时刻(t=T)的价格分别是S1,S2,…,Sn.记xi=ln(Si/Si0),i=1,2,…,n,Xn×1= (x1x2…xn)T,其中xi是第i种证券从时间t=0到t=T这段时间的对数收益率,X是n种证券的对数收益率向量.这里S10,S20,…,Sn0是已知常数,而S1,S2,…,Sn都是随机变量,所以x1,x2,…,xn是随机变量,而X是一个随机向量,则它的期望和协方差矩阵用符号表示为

设第i种证券的投资比例为ωi,i=1,2,…,n.记ωn×1= (ω1ω2…ωn)T,en×1= (11 …1)T,要求投资比例满足条件ωTe=1.投资者对应于投资比例ω的投资收益为R=ωTX,R是一个随机变量,其期望收益和方差分别为
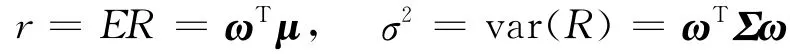
Markowitz的均值-方差模型就是考虑下面的条件极值问题[2]:
(1)指定收益ωTμ=r0下,求ω使风险最小,即var(ωTX)=ωTΣω最小;
(2)指定风险ωTΣω=σ20下,求ω使收益最大,即ωTμ最大.
显然两者等价,这里用问题(1)进行研究,归结为如下规划问题:在ω满足ωTe=1和ωTμ=r0的条件下,求ωTΣω达到最小值的解.求得其解为,则ωT*X对应的方差,投资学中称上式为投资组合的有效前沿.其中
本文应用无差异曲线法先求出具有该类型效用函数的投资者的最大期望收益,然后根据均值-方差模型推导投资者的最优组合投资决策方案,并求相应的组合投资比例.
1 模型建立
由ai>0,i=1,2,3,则双指数效用函数的一 阶 导 数U′=a1(a2exp (-a2(R-c2))+a3exp(-a3(R-c2)))>0,效用递增,且U″=a1(-a22exp(-a2(R-c2))-a23exp (-a3(R-c2)))<0,则U为凸函数,即它是风险厌恶型的.在通常情况下,若采用双指数效用函数,当投资者面临一个无穷投资序列时,投资者通过最大化期望效用来使其回报率最大化.
金融数学理论中已证明并约定投资收益R服从正态分布N(r,σ2),且r、σ2如前,则双指数效用函数的数学期望为

可求得
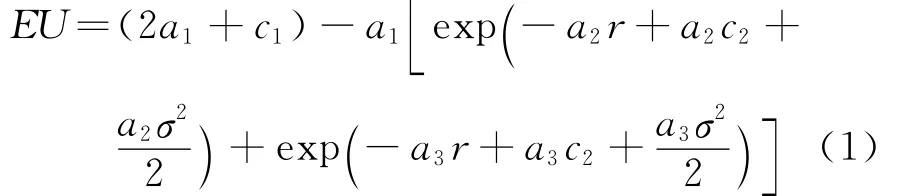
因该效用函数为风险厌恶型,则应用投资学中的无差异曲线法进行求解.按照无差异曲线的理论[3~8],双指数效用函数的期望效用EU是一无差异曲线族,应用均值 -方差模型原理,建立如下模型:
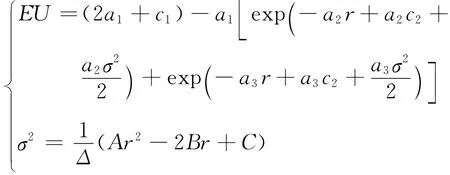
此模型意义为投资者会在组合投资可供选择的有效前沿里尽量选择使期望效用最大的投资收益,即最优组合为有效前沿与效用尽可能最大的无差异曲线的切点.原理如图1所示.

图1 最优组合的选择Fig.1 Optimal portfolio selection
图1中I1、I2、I3分别表示效用不同的无差异曲线(即等效用曲线),向右开口的抛物线表示有效前沿,即投资者组合投资的有效组合构成的集合,所以投资者的最优组合即是有效前沿与效用尽可能最大的无差异曲线的切点.
2 最优决策求解
对上述模型进行分析,将有效前沿σ2代入期望效用EU中,可得
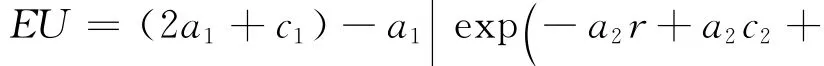
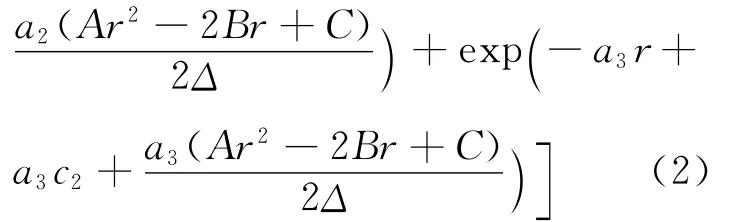
首先求得该期望效用函数的最大值点,进而求得最优投资组合比例.
由于ai> 0,i= 1,2,3,在 区 间内

则期望效用EU必有最大值.
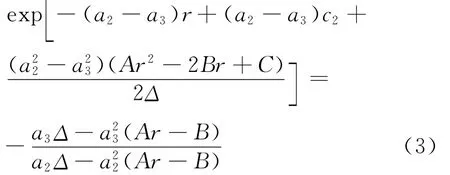
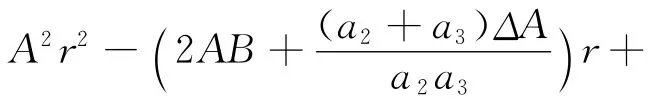

对二次不等式(4)的解推导可作如下讨论:
(1)当a2>a3时,解位于
(2)当a2<a3时,解位于
综上可得解位于

下面对方程(3)的解作如下讨论:
(a)当a2>a3时,式(3)为

两边取对数整理得
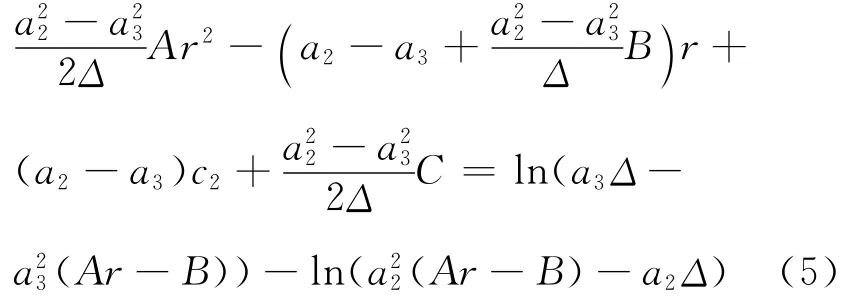
先判断方程(5)解的情况,令方程左侧为y1,右侧为y2,则y1为开口向上的抛物线,其对称轴为

图2 a2>a 3时根的判定Fig.2 Determination of the root when a2>a3
(b)当a2<a3时,式(3)为

两边取对数整理得

先判断方程(6)解的情况,令方程左侧为y1,右侧为y2,则y1为开口向下的抛物线,其对称轴为
(c)当a2=a3时,此时效用函数为单指数函数
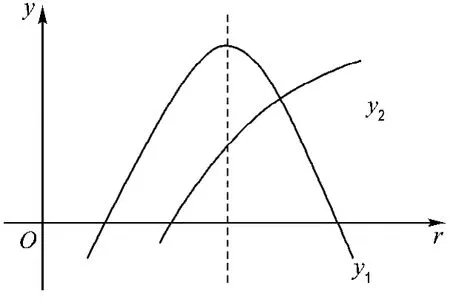
图3 a 2<a3时根的判定Fig.3 Determination of the root when a2<a3
此类效用函数在其他文献中有过介绍,所以本文可看作此类问题的一种推广模型.
综合以上3种情况可知,在确定了期望收益r后,根据均值-方差模型中推出的公式就可求出最优组合的投资比例.
3 实际应用举例
设有5种证券,收益的期望值为μ=(0.2080.3530.2620.1670.318)T.
收益率的协方差矩阵

其中根据数据可求得A=46.5979,B=9.6042,C=2.1580,Δ=8.3204.
以下根据两种情况展开应用:
(a)当a2≠a3时,不失一般性,取a1=a2=c1=c2=1,a3=2.

(b)当a2=a3时,不失一般性,取a1=a2=a3=c1=c2=1,此时效用函数为单指数函数U=1+2(1-exp(-(x-1))).因此可求得r=0.3847,进而求得最优组合的投资比例ω=(0.04010.74530.0875 - 0.33070.4574)T.
4 结 论
本文应用无差异曲线法,较好地解决了具有双指数效用函数的最优组合决策问题,给出了其组合投资的最优决策,这对组合投资理论研究和投资者实践操作具有一定的指导意义.
[1]MARKOWITZ H.Portfolio selection[J].Journal of Finance,1952(7):77-91
[2]张尧庭.金融市场的统计分析[M].桂林:广西师范大学出版社,1998:36-44
[3]叶中行,林建忠.数理金融——资产定价与金融决策理论[M].北京:科学出版社,1998:21-23
[4]《运筹学》教材编写组.运筹学[M].3版.北京:清华大学出版社,2005:417-430
[5]威廉·F·夏普,戈登·J·亚历山大,杰弗里·V·贝利.投资学[M].5版 上.北京:中国人民大学出版社,1998:102-105
[6]周庆健,吴建民.负指数效用函数最优组合的两种解法及其一致性[J].大连民族学院学报,2004,6(1):7-10
[7]张鸿雁,岳 妍.典型效用函数下最优投资消费问题[J].统计与决策,2007(20):18-20
[8]贺学会,陈 洋.效用函数与行为人:一个金融经济学视角的诠释[J].财经理论与实践,2008,29(5):2-7

