自锚式吊拉组合体系桥主缆线形计算方法

张 征， 黄 才 良， 张 哲

（1.大连理工大学 桥梁工程研究所，辽宁 大连 116024；2.山东科技大学 土木建筑学院，山东 青岛 266510）

0 引 言

自锚式吊拉组合体系桥是一种以柔性缆索作为主要承重构件的桥梁，其结构刚度小，在外部荷载作用下结构变形大.作为主要承重构件之一的主缆，其线形和无应力长度的精确计算是结构在成桥后几何线形能够满足设计要求的必要条件.目前针对吊拉组合体系桥的研究主要集中在设计探索和结构体系分析上[1～4]，所需计算主要采用大型有限元软件如ANSYS、ALGOR、ADINA等进行，但这些软件基本上是通用软件，对自锚式吊拉组合体系桥的分析比较麻烦，如ANSYS没有专门用于缆索分析的索单元，只能采用杆单元（Link10）来模拟，且非线性计算往往不容易收敛，对缆索的无应力长度更是无法计算.此外，对于索鞍预偏量的计算、切点位置变化预测及计算，通用软件很难进行有效的分析和模拟.在目前自锚式吊拉组合桥的计算理论研究中，专门针对自锚式吊拉组合桥主缆线形和主缆无应力长度计算的文献还没有见到.

本文在悬索桥主缆线形计算方法研究的基础上[5～9]，结合自锚式吊拉组合体系桥的施工和受力特点，给出其主缆线形计算的数值解析法，并在此基础上考虑索鞍的影响，编制相应的计算程序.

1 主缆线形计算的分段悬链线理论

1.1 自重均布荷载作用下的索段分析

1.1.1 索段基本方程[5]如图1所示的悬索段，当只有沿无应力索长均布的自重荷载q作用时，索段为悬链线.则满足边界条件的索段基本方程为

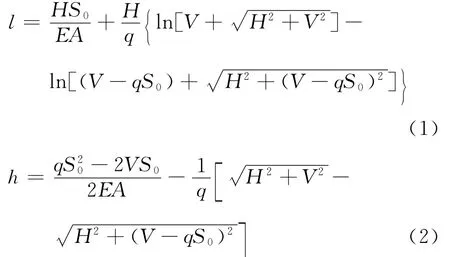
式中：E为索弹性模量；A为索截面面积；S0为索段无应力长度；l为索段两端点的水平间距；h为索段两端点的高差.

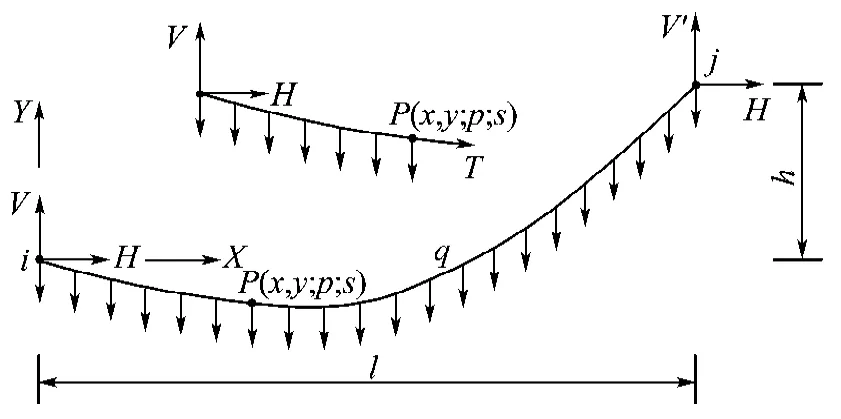
图1 自重荷载作用下的悬索段Fig.1 Segment of cable under self－weight

1.1.2 索段线形变化刚度 对式（1）、（2）求l和h的全微分，得

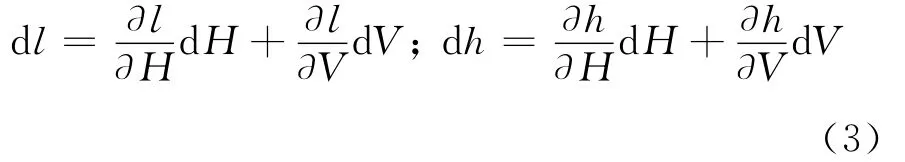
令

则f11、f12、f21、f22分别为

将式（3）用dl和dh表示dH和dV，并写成矩阵形式为

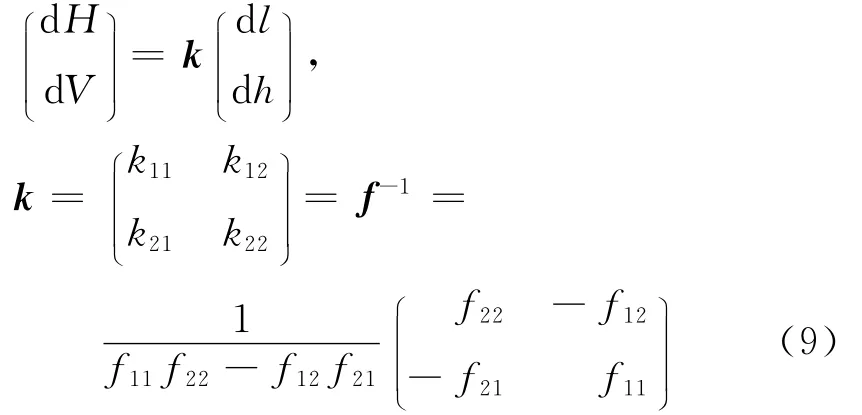
式（9）中的矩阵k即为索段的线形变化刚度矩阵，表达了索段的内力变化量与线形变化量间的关系.

1.2 自重和竖向集中力作用下的悬索分析

有竖向集中外荷载作用的主缆如图2所示，

其受力图示相当于很多1.1.1中的基本索段相连，并在连接点i作用有竖向集中荷载P i.悬索在各分点需满足的力学平衡条件为

式中：n为索段数，Hl（i）、Hr（i）分别为i索段左右端点的水平分力；Vl（i）、Vr（i）分别为i索段左右端点的竖向分力；S0i为i索段的无应力索长；Pi为作用在i索段右端点处的竖向集中力.

图2 自重和竖向集中力作用下的悬索Fig.2 Cable under self－weight and vertically concentrated forces

1.3 一跨主缆的线形变化刚度

在悬索所受外荷载不变的情况下，如果某分点的内力发生变化，则其他分点的内力也将发生变化，且变化量相同.若支点的位置和标高不变，从悬索支点到m分点之间的各索段的累计线形变化量即为m分点的线形变化量，即

按照上述索段刚度矩阵的建立方法可得悬索m分点的内力变化量与线形变化量的刚度矩阵：

K即为主缆的线形变化刚度矩阵，f11、f12、f21、f22根据式（5）～ （8）求得.

当主缆一端的水平分力已知时，式（11）中dH＝0，经过推导可得到此时主缆的线形变化刚度为

2 主缆线形计算

2.1 成桥状态主缆线形计算

成桥状态主缆线形具体迭代计算过程见图3.

主跨始端点处的水平分力和竖向分力的迭代初值Hl（1）、Vl（1）按下式给出：

式中：L为主跨主缆水平跨度；C为主跨主缆两端点的高差；w为按照抛物线理论计算的荷载集度，

2.2 空缆状态线形和索鞍预偏量的计算

2.2.1 索鞍预偏量ΔD的增量刚度方程 为使索鞍沿滑移面平衡，根据索鞍两侧不平衡力F计算索鞍的偏移修正量为

式中：K＝ （K11＋K′11）cos2α＋（K12＋K′12＋K21＋K′21）sinαcosα＋（K22＋K′22）sin2α＋Kt.其中K11、K12、K21、K22分 别 为 索 鞍 左 侧 主 缆 刚 度 系数，K′11、K′12、K′21、K′22分别为索鞍右侧主缆刚度系数，Kt为桥塔或支墩沿索鞍滑移面方向的抗推刚度.式（15）表达了索鞍处沿滑移面不平衡分力与索鞍移动量之间的关系.在索鞍预偏量计算时，由于索鞍沿支承滑移面放松，这时候只要Kt＝0即可.

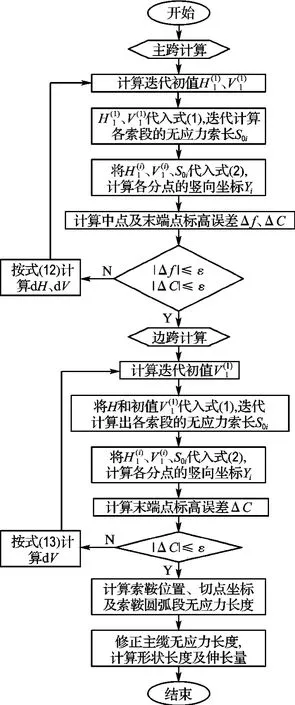
图3 成桥状态计算流程图Fig.3 Calculation flow chart of finished bridge state

2.2.2 空缆线形计算 空缆线形的计算就是在保证无应力长度不变的前提下，寻找一组索鞍预偏量，使得主缆在索鞍处满足平衡条件.本文在计算时始终采用的是理论顶点（空缆状态的理论顶点仍定义为索鞍两侧主缆切点顺延悬链线的交点）的预偏量，在求出理论顶点的预偏量之后，再最终求得索鞍的预偏量.计算时首先假定单个索鞍理论顶点处的水平预偏量（其余索鞍固定），这样，预偏理论顶点两侧主缆的跨度和各控制点的坐标就确定了，然后分别对两侧主缆进行计算，最后校核该索鞍处是否满足：索鞍两侧水平分力相等；索鞍竖向位置与成桥状态的关系合理；索鞍两侧主缆无应力长度与成桥状态相等.然后再按上述方法依次计算其余索鞍的预偏量，直至各个索鞍均满足上述要求.具体迭代计算过程见图4.

空缆状态下，为了使迭代过程快速收敛，理论顶点两侧主缆的水平分力H（1）l和竖向分力V（1）l的迭代初值可按如下取值：

β由下式确定：

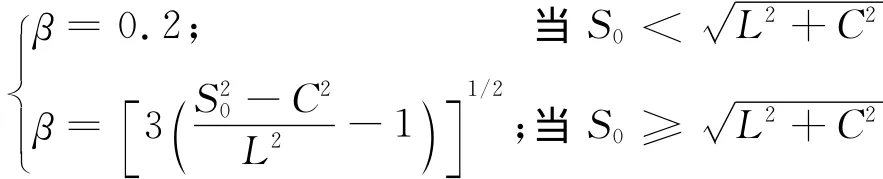
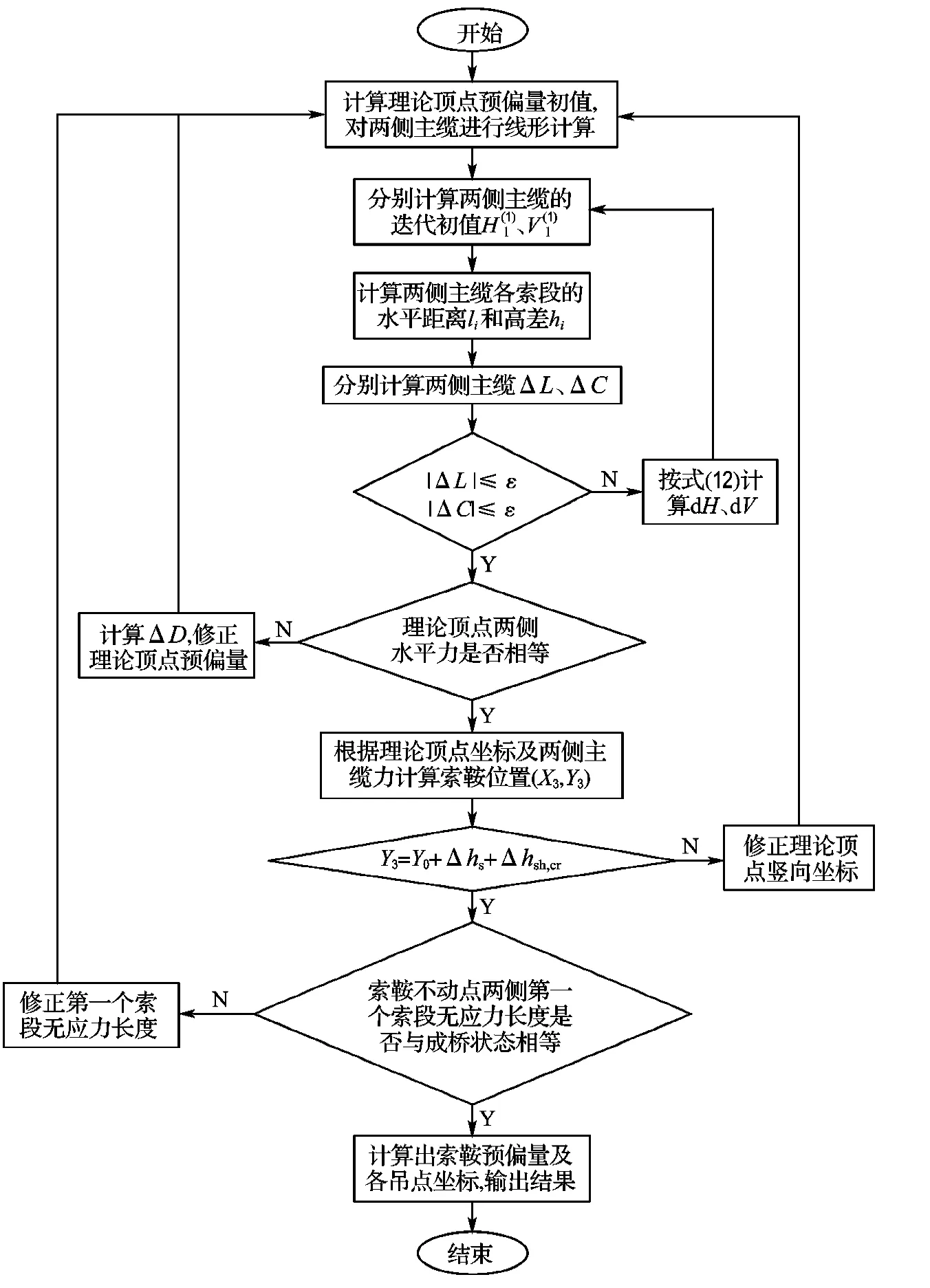
图4 空缆状态计算流程图Fig.4 Calculation flow chart of cable－finished state

本文提出了一种关于主缆空缆线形计算的新方法，其优点如下：

①空缆状态线形与成桥状态线形的计算方法完全相同，不需再另外编写程序；

②空缆状态索鞍位置与成桥状态索鞍位置的计算方法完全相同，不需再另外编写程序；

③所有计算均为一种精确的计算，没有多余的人为假定.

3 算 例

3.1 经典例题验证

有一柔索，采用量纲一计算技术.标准温度下其无应力长度S0＝100，抗拉强度EA＝3×107，沿索自重荷载为q＝1，线胀系数为6.5×10－6，在温度升高100℃的情况下，索O端固定，另一端分别沿着x＝20，40，60，80，100，则索端力与对应的索端位置的关系如图5所示，具体计算结果见表1.

图5 不同索端位置对应的线形图Fig.5 Cable shape drawing at different cable ends

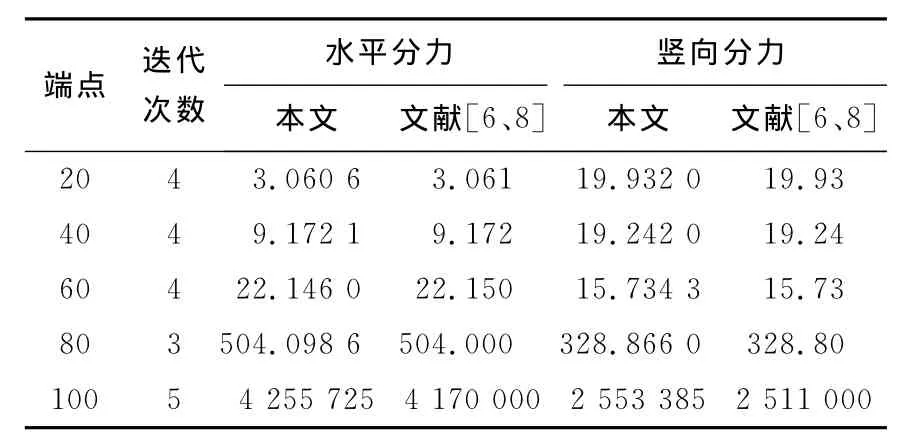
表1 各索端位置对应的索端力Tab.1 Cable－end force at different cable ends

为了绘制出索的线形，本文采用100个索单元进行模拟，对x＝20，40，60，80，100进行计算，收敛精度取1×10－5.从表1可见，除x＝100外，本文的结果与文献[6、8]非常接近，但x＝100的结果却相差较大.通过对文献[6、8]的结果复核表明，其结果是错误的.因为F y/F x＝0.60216大于索两端弦线的斜率0.6，这显然是不正确的，因为在索的自重作用下，其右端的切线斜率必然小于其弦线的斜率.从表1中的迭代次数可以看出，本文计算程序具有所需迭代次数少、收敛速度快的特点.

3.2 工程算例验证

大连市金州海湾大桥设计方案[10]为132 m＋400 m＋132 m自锚式吊拉组合体系桥.矢跨比为1/6.667.本文分别采用上述自编程序和Ansys有限元法对该桥主缆无应力长度和索鞍预偏量以及成桥线形进行计算，其结果比较分别见表2和表3.

表2 主缆无应力长度和索鞍预偏量计算结果比较Tab.2 Results comparison of unstressed length and saddle predisplacement

表3 成桥状态主缆线形计算结果比较（半桥）Tab.3 Results comparison of main cable shape under finished bridge state（half bridge）

上述结果表明本文方法计算结果与有限元方法计算结果具有较好的一致性.

4 结 论

（1）使用本文方法进行主缆线形计算，数据输入简单明了，迭代收敛速度较快.

（2）采用本文编制的程序可以进行成桥状态主缆线形、空缆状态主缆线形和索鞍预偏量等一整套设计所需参数的精确计算，并且可以计算任意跨数的主缆线形.

（3）与有限元法相比，本文方法可以精确考虑索鞍的影响，使计算模型更接近于实际结构，对设计、施工和科研具有很好的参考价值.

（4）本文所编制的程序不只可以进行自锚式吊拉组合桥的线形计算，对于地锚式吊拉组合桥以及地锚和自锚式的悬索桥均可以进行计算.

[1]蒙 云，孙淑红.吊拉组合桥结构体系研究与决策[C]//中国公路学会桥梁和结构工程学会一九九九年桥梁学术讨论会.厦门：中国公路学会桥梁和结构工程学会，2000：691－697

[2]张 哲，王会利，黄才良.自锚式斜拉－悬索协作体系桥梁设计与分析[J].公路，2006（7）：44－48

[3]张新军，张 丹 .吊拉组合体系桥的研究进展[J].浙江工业大学学报，2007，35（5）：553－558

[4]肖汝诚，贾丽君，薛二乐.斜拉－悬吊协作体系桥的设计探索[J].土木工程学报，2000，33（5）：46－51

[5]IRVINE H M.Cable Structures[M].Cambridge：The MIT Press，1981

[6]唐茂林.大跨度悬索桥空间几何非线性分析[D].成都：西南交通大学，2003

[7]KIM Ho－kyung，LEE Myeong－jae，CHANG Sungpil. Nonlinear shape－finding analysis of a selfanchored suspension bridge [J]. Engineering Structures，2002，24（6）：1547－1559

[8]李传习.混合梁悬索桥非线性精细计算理论及其应用[D].长沙：湖南大学，2006

[9]罗喜恒.悬索桥缆索系统的数值分析法[J].同济大学学报，2004，32（4）：441－446

[10]吴宏业.自锚式斜拉－悬索协作体系桥静力性能分析[D].大连：大连理工大学，2006