波浪作用下柔性靠船墩船舶撞击力统计分析

王 建 超， 贡 金 鑫， 冯 云 芬

（大连理工大学 土木工程学院，辽宁 大连 116024）

0 引 言

随着世界经济的高速发展，各国之间的贸易往来越来越频繁，特别是石油、铁矿石和钢铁等货物的运输更是如此.这些大宗货物通常都是通过海上运输，并且运输距离比较远，在这种情况下，采用超大型船舶无疑会具有非常明显的经济效益.然而大型和超大型船舶的发展，也对码头的建设提出了新的要求，导致码头建设开始向着自然条件相对恶劣的外海深水地区发展.

目前国内外外海大型开敞式码头的结构型式，还是以重力墩式和桩基结构为主，但当水深进一步增加后，传统的重力式结构和桩基结构在技术和经济上均受到了很大制约，需要研究新的码头结构型式，本文所分析的柔性靠船墩就是这样一种新型轻型码头结构，类似于钢导管架结构.

目前，在世界范围内基于可靠性理论的概率极限状态设计方法在建筑、桥梁、水工结构和公路桥梁的设计中得到了广泛应用.在北美，概率极限状态设计方法获得了很好的发展并应用于几乎所有结构设计中[1～4].对于外海轻型码头结构，波浪作用下船舶撞击力是其所遭受的主要荷载之一.由于轻而柔，受到船舶撞击后，靠船墩的变形不可忽略.我国港口工程结构设计目前采用的是以概率理论为基础的极限状态设计方法，轻型码头设计也应以可靠度方法为基础，因此研究波浪作用下船舶撞击力的概率统计分布，建立荷载概率分布模型，显得十分重要.由于这种结构型式目前还处在研究阶段，而且结构的刚度也比较小，在计算统计参数时应考虑靠船墩刚度的影响，在这方面目前国内外还较少有人考虑，本文就是以此为背景，对波浪作用下的船舶撞击力进行统计分析.

1 船舶有效撞击能

系泊船舶在波浪作用下引起的撞击力与很多因素有关，计算非常复杂，《港口工程荷载规范》（JTJ 215—89）给出了船舶在横浪作用下撞击能的计算公式，即

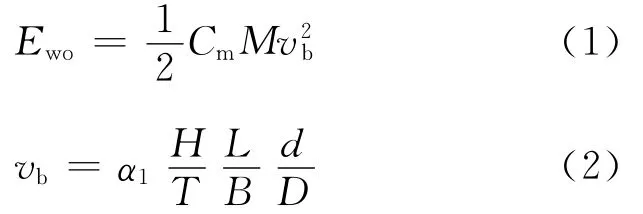
式中：Ewo为横浪作用下系泊船舶有效撞击能（kJ）；M为船舶质量（t），按与船舶计算装载度相应的排水量计算；Cm为船舶附加水体质量系数；α1为系数（橡胶防冲设施取用0.2）；vb为横浪作用下系泊船舶对码头撞击的法向速度（m·s－1）；H为波高（m），按船舶不离开码头的最大波高计算；B为船宽（m）；D为船舶平均吃水（m）；d为码头前沿水深（m）；L为波长（m），计算公式为

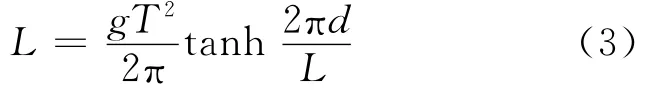
其中T为平均周期（s）.

将式（2）和（3）代入式（1），得

式（4）是系泊船舶撞击能的基本公式，但《港口工程荷载规范》（JTJ 215—98）对式（4）做了适当调整，将d/D的幂次改为2.5，并将系数α1提高到0.22，为表达方便，系数α21/4π近似取为0.004，得到系泊船舶有效撞击能Ewo的计算公式为

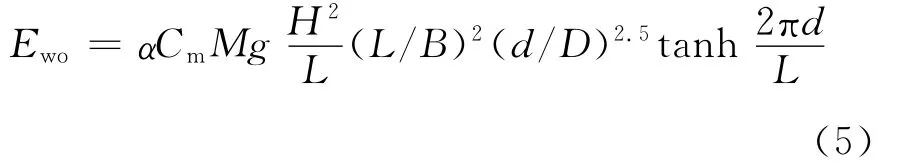
其中α取0.004.

当系靠船结构物由多个靠船墩组成时，分配在每个靠船墩上的有效撞击能Ew按下式计算：

式中：n为靠船墩数目；K为靠船墩之间有效撞击能分配不均匀系数.

将式（5）代入式（6），得

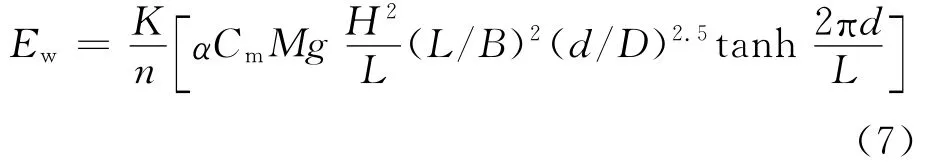
2 船舶有效撞击能的统计分析

式（7）中α、Cm、K和H应当作随机变量来考虑，下面对它们分别进行统计分析.

2.1 α、C m和K的统计分析

文献[5]通过对已有试验数据的统计分析，给出了α、Cm和K的统计参数和概率分布类型，如表1所示.

2.2 波高H的统计分析

文献[6]利用渤海海域波浪要素的观测结果，给出波高的统计资料，如表2所示，表中αH和u H分别为波高H极值Ⅰ型分布函数的参数；珨H和δH为波高的均值和变异系数.

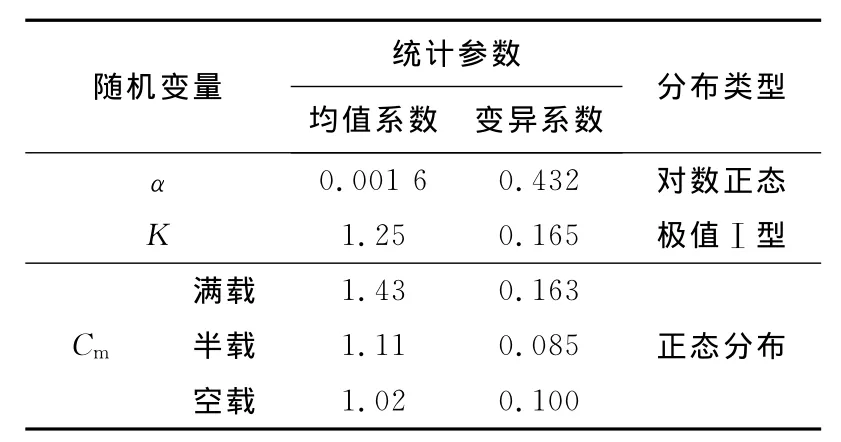
表1 α、C m和K的统计参数和概率分布类型Tab.1 Statistical parameters and probability distribution ofα，C m and K

表2 波高的统计参数Tab.2 Statistical parameters of wave height

2.3 有效撞击能的统计参数

如果已知上面各随机变量的统计参数，则可计算有效撞击能的统计参数.由式（7）得

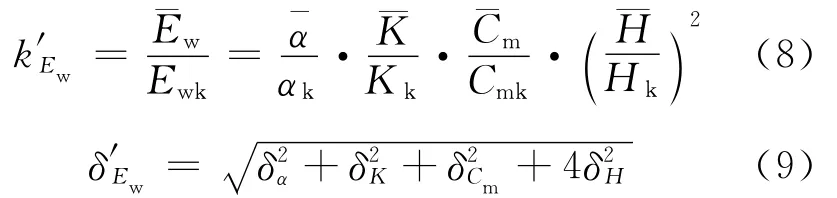
按《港口工程荷载规范》（JTJ 215—89），取αk＝0.004，Kk＝1.8，满载时Cmk＝1.45，半载时Cmk＝1.25，空载时Cmk＝1.05.将以上数据代入式（8）和（9），就可以得到在不考虑模型不定性时有效撞击能的统计参数，如表3所示.

由表3可以看出，有效撞击能的均值系数比较小，原因是参数α的标准值比较大，文献[7]通过试验得到α1的均值为0.14，荷载规范JTJ 215—89取为0.2，而荷载规范JTJ 215—98取为0.22，本 文 为 了 计 算 方 便 把α21/4π 近 似 取 为0.004，这相当于间接把α1的标准值取为0.224，所以有效撞击能的均值系数偏小.

表3 有效撞击能统计参数（不考虑模型不定性）Tab.3 Statistical parameters of efficient impact energy（without considering the uncertainty of model）

当考虑计算模型的不定性时，用Kp来表示有效撞击能计算模型的不定性，则

式中：Ew为有效撞击能试验值；Ewk为按照规范公式计算得到的有效撞击能.根据文献[7]的实测数据得到，满载时，Kp的均值珡Kp＝0.74，变异系数δKp＝0.48；半载时，Kp的均值为0.58，变异系数为0.43；空载时，Kp的均值为0.47，变异系数为0.64.考虑计算模型不定性后，有效撞击能的统计参数可以表示为

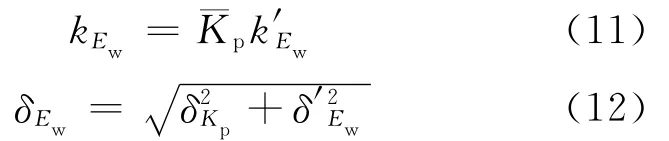
表4为考虑模型不定性后有效撞击能的统计参数.

表4 有效撞击能统计参数（考虑模型不定性）Tab.4 Statistical parameters of efficient impact energy（considering the uncertainty of model）

由表4可以发现，由两个不同海区计算得到的有效撞击能的均值系数和变异系数差别不大，所以本文为方便计算，取两个海区均值系数和变异系数的平均值作为有效撞击能的统计参数.经计算，1 a内：k Ew＝0.081，δEw＝0.779；50 a内：k Ew＝0.173，δEw＝0.741.

2.4 有效撞击能的概率分布

采用Monte－Carlo随机抽样的方法，对有效撞击能的概率分布进行统计分析[8].计算时，首先根据α、Cm、K和H的概率分布函数进行随机数抽样，再将产生的α、Cm、K、H的样本值代入式（8）中得到k′Ew的样本值，对样本值进行统计分析和K－S检验，就可以得到波浪作用下船舶撞击能的概率分布模型.

本文模拟产生了10000个随机样本值，对其进行拟合优度检验，取显著性水平α＝0.05，经KS检验，有效撞击能不拒绝服从对数正态分布[9].图1为3种概率密度函数的比较图，通过以上分析可以认为有效撞击能的概率分布模型为对数正态分布.

图1 有效撞击能的概率分布Fig.1 Probability distribution of efficient impact energy

3 船舶撞击力的统计分析

由于码头的靠船墩用钢管焊接而成，属于柔性结构，靠船墩在受到船舶撞击后需考虑其变形.

3.1 波浪作用下船舶撞击力的计算

根据虚功原理，船舶有效撞击能应等于船体、平台和护舷3个部分变形吸收的能量之和，即

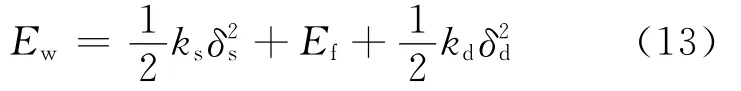
式中：Ef为护舷吸收的能量；ks、kd分别为船体和平台的弹性刚度系数；δs、δd分别为船体和平台的变形.

根据弹性变形理论，船舶撞击力的计算公式为

式中 ：Ff为护舷反力（k N）；Fx为船舶靠岸撞击力（k N）.

将式（14）代入式（13），可得

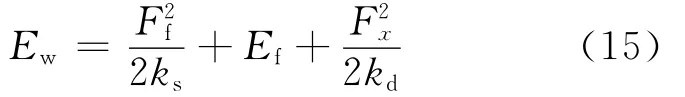
即

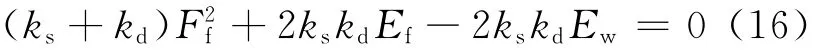
由式（16）可以看出，当已知船舶有效撞击能时，护舷的反力Ff随着护舷吸收能Ef的变化而变化，所以计算护舷反力时需要确定其与吸收能量之间的关系.

对于外海开敞式码头结构，常用的护舷型式是鼓型护舷，图2为YGCH3000型护舷的变形性能曲线[10].从图2可以看出，橡胶护舷反力和吸收能量都与护舷变形呈非线性关系.由图2就可以确定护舷反力与吸收能之间的关系.图3中的实际曲线为YGCH3000（RL）型护舷的吸收能－反力曲线.

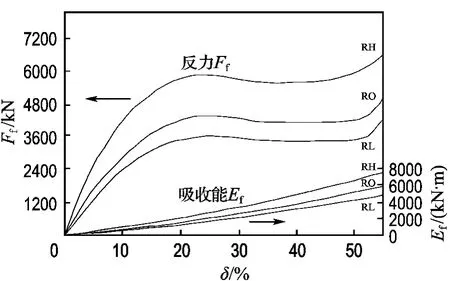
图2 YGCH3000型护舷性能曲线Fig.2 Performance curve of YGCH3000 fender

图3 实际曲线与拟合曲线比较Fig.3 Comparison of active curve and fitted curve

从图3可以看出，护舷吸收能－反力呈非线性，本文采用分段拟合的方法，根据曲线的形状，将曲线分成3段，应用最小二乘原理[11]对每一段分别进行三次多项式拟合，为了保证曲线通过原点并且在分段点处连续，分别选取下面的3个分段函数：

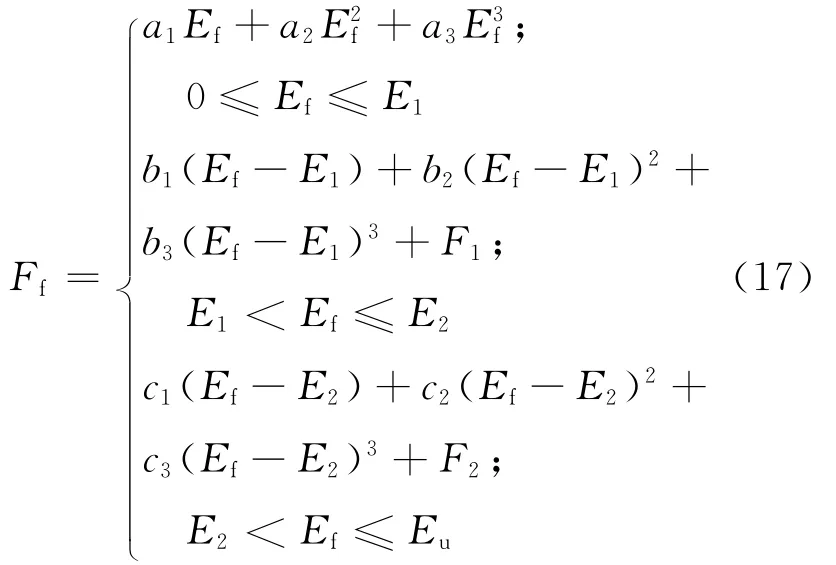
式中：a1～a3、b1～b3和c1～c3分别为3个分段方程的系数；E1、F1为第一段拟合方程在第一个分段点处的函数值；E2、F2为第二段拟合方程在第二个分段点处的函数值；Eu为护舷的最大吸收能.

本文根据 YGCH3000（RL、RO、RH）3种鼓型护舷的变形性能曲线，通过计算得到其吸收能－反力拟合公式为

图3示出了拟合曲线与YGCH3000（RL）型护舷的实际吸收能－反力曲线的比较.由图可见拟合曲线与实际曲线非常接近.

将式（18）代入式（16），得到关于护舷吸收能Ef的六次方程，求解该非线性方程即可求出护舷吸收能，再根据式（18）可计算船舶的撞击力.本文采用对分法求解非线性方程.

3.2 波浪作用下船舶撞击力的统计分析

在计算船舶撞击力的概率分布时，首先根据规范计算出有效撞击能的标准值，用标准值去乘有效撞击能的均值系数，就可以得到有效撞击能的平均值；其次根据有效撞击能的平均值、变异系数和概率分布函数，采用Monte－Carlo模拟产生有效撞击能的样本值；最后根据3.1节的方法计算撞击力的样本值，对样本进行统计分析，即可得到撞击力的统计参数和概率分布模型.

对100000 DWT油轮满载状况下进行分析.船舶尺度与参数的标准值[12、13]分别取为M＝125000 t，H＝2.0 m，L＝2.0 m，B＝40.8 m，d＝21.5 m，D＝15.5 m，α＝0.004，Cm＝0.004，K＝1.8，n＝2.0.

根据文献[14]，船体的弹性刚度系数ks近似取为9.0×104k N/m，由于轻型码头为柔性结构，当刚度比不同时，撞击力的统计参数也不同.在确定撞击力的统计参数时，以YGCH3000（RO）型护舷的初始刚度为基准刚度，取靠船墩的刚度为5、10、20、30、40、50、60和70倍的基准刚度.

表5～7给出了在1 a和50 a内，YGCH3000（RL、RO、RH）3种型式护舷在不同刚度比情况下船舶撞击力的统计参数.

对YGCH3000（RL、RO、RH）3种护舷在不同刚度比下的统计参数进行平均，得到1 a和50 a内波浪作用下船舶撞击力的统计参数，结果如表8所示，其分布类型为极值Ⅰ型.

表5 船舶撞击力的统计参数（YGCH3000（RL））Tab.5 Statistical parameters of ship impact force（YGCH3000（RL））

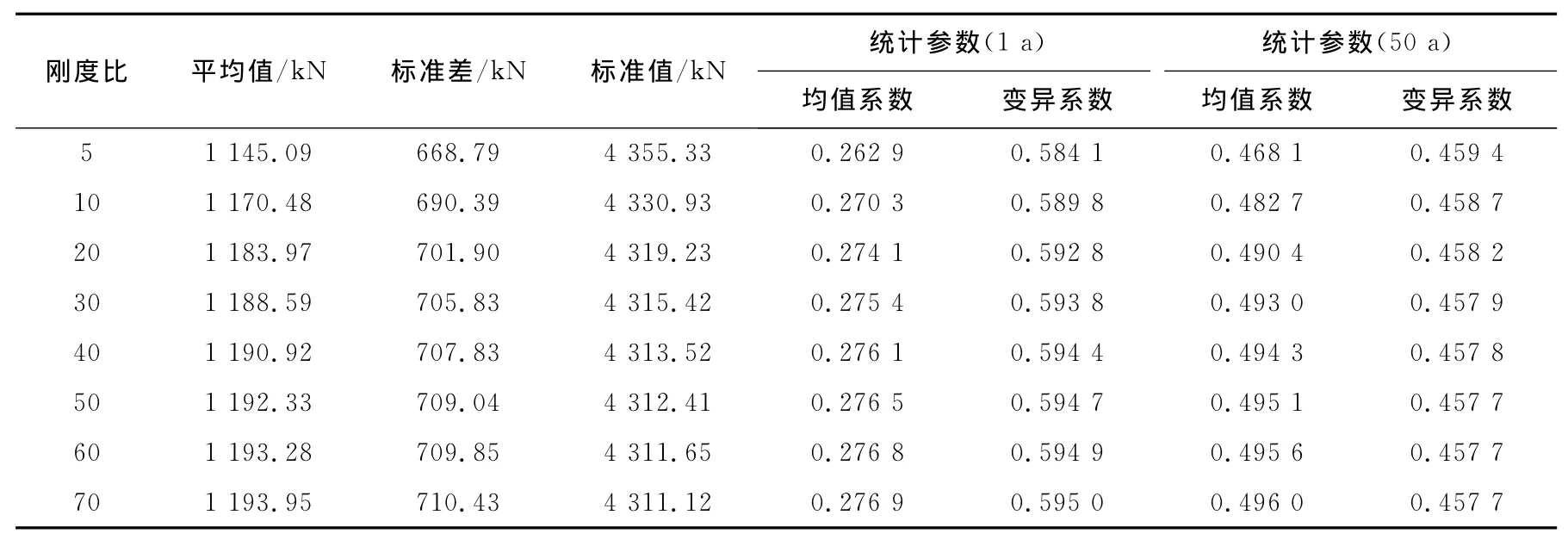
表6 船舶撞击力的统计参数（YGCH3000（RO））Tab.6 Statistical parameters of ship impact force（YGCH3000（RO））

表7 船舶撞击力的统计参数（YGCH3000（RH））Tab.7 Statistical parameters of ship impact force（YGCH3000（RH））

表8 船舶撞击力统计参数Tab.8 Statistical parameters of ship impact force

采用上面相同的计算方法对YGCH2500（RL、RO、RH）3种护舷在不同刚度比下船舶撞击力的统计参数进行了计算，计算结果与表8相差不大，所以可以将表8的计算结果作为船舶系泊撞击力的统计参数.

在研究波浪作用下船舶撞击力的概率分布时，取靠船墩刚度为15倍的基准刚度.采用Monte－Carlo方法进行随机抽样，模拟产生了10000个随机样本值，对其进行拟合优度检验，取显著性水平α＝0.05，经K－S检验，船舶撞击力不拒绝服从极值Ⅰ型分布.图4为YGCH3000（RL）型护舷所对应的撞击力概率分布的比较图，本文选极值Ⅰ型分布作为波浪作用下船舶撞击力的概率分布.

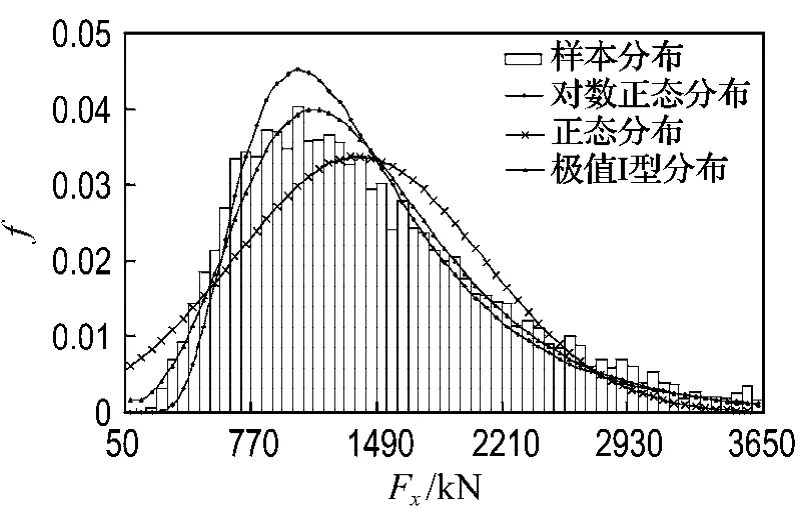
图4 船舶撞击力概率分布Fig.4 Probability distribution of ship impact force

4 结 论

（1）在设计基准期1 a和50 a内，波浪作用下船舶撞击能和撞击力的概率分布函数可以分别用对数正态分布和极值Ⅰ型分布来描述.

（2）设计基准期1 a内，船舶撞击力的均值系数为0.297，变异系数为0.566；设计基准期50 a内，船舶撞击力的均值系数为0.511，变异系数为0.429.

[1]BYFIELD M，NETHERCOT D.Safety variations in steel designed using Eurocode 3 [C]// JCSS Workshop on Reliability Based Code Calibration.Swiss：Swiss Federal Institute of Technology Press，2002

[2]GULVANESSIAN H， HOLICKY M.Reliability based calibration of Eurocodes considering a steel member[C]//JCSS Workshop on Reliability Based Code Calibration.Swiss：Swiss Federal Institute of Technology Press，2002

[3]TREZOS C G，THOMOS G C.Reliability based calibration of the Greek seismic code[C]//JCSS Workshop on Reliability Based Code Calibration.Swiss：Swiss Federal Institute of Technology Press，2002

[4]SADOVSKY Z.Probability based design codes in Slovakia－historical development and new challenges[C]//JCSS Workshop on Reliability Based Code Calibration.Swiss Federal Institute of Technology Press，2002

[5]贡金鑫，王建超.海外轻型码头荷载统计分析[R].大连：大连理工大学，2009

[6]王欣平.海洋环境随机荷载与平台结构可靠度分析[D].哈尔滨：哈尔滨建筑大学，2000

[7]王欣平.关于波浪作用下码头船舶荷载问题的探讨[J].水利水运学报，1976，1（1）：1－39

[8]贡金鑫.工程结构可靠度计算方法[M].大连：大连理工大学出版社，2003

[9]滕素珍，冯敬海.数理统计学[M].大连：大连理工大学出版社，2005

[10]顾民全.海港工程设计手册[M].北京：人民交通出版社，2001

[11]魏毅强，张建国，张洪斌.数值计算方法[M].北京：科学出版社，2005

[12]交通部第一航务工程勘察设计院，交通部第二航务工程勘察设计院.JTJ 215—98港口工程荷载规范[S].北京：人民交通出版社，1998

[13]陈际丰，刘 强，牛恩宗.波浪作用下船舶撞击力计算参数的选择[J].水运工程，2007，11：6－9

[14]陆文发，李林普，高道明.近海导管架平台[M].北京：海洋出版社，1992