关于折叠超立方体的反馈数

徐 喜 荣， 曹 楠， 吉 日 木 图， 董 学 智， 王 保 才， 王 磊

（1.大连理工大学 计算机科学与技术学院，辽宁 大连 116024；2.中国科学技术大学 数学系，安徽 合肥 230026；3.内蒙古民族大学 数学学院，内蒙古 通辽 028043）

0 引 言

对简单图（有向或无向）G＝ （V，E），F是顶点集合V（G）的子集，如果从顶点集合V中删除子集F后，剩余顶点的导出子图不含（有向或者无向）圈，则称F是G的反馈点集.点数最小的子集F称为最小反馈点集.

图的最小反馈点集问题来源于实际问题.例如，在互联网中，终端电脑作为节点，终端之间的连线作为边，则可以用图来建立互联网的数学模型，网络中的某些性质可以用图论的参数来刻画.如果网络中某些节点发生故障，则极易使网络陷入瘫痪状态，为了避免此情况的发生，网络设计中允许存在一些回路.由于不同的网段之间是以网桥相互连接，广播消息通过网桥从一个网段传播到下一个网段.若网络中存在回路，则广播消息会在网桥环网中一直传递下去，形成“广播风暴”.为了避免形成网络中的“广播风暴”，则需要尽可能少地关闭一些网桥，使剩余的网络不再含有回路.用图论术语来说，就是要确定该网络对应图的一个最小反馈点集.

在操作系统和超级计算机的分布式计算中经常出现死锁问题.操作系统中的死锁可以用状态图来描述.若状态图中包含回路，则系统中的进程将出现资源互相等待的状态，极易产生死锁问题.一个著名的解决死锁问题的方法是在对应的状态图中放弃尽可能少的进程，等价于在状态图中找到尽可能少的点，去掉这些点后，剩余的状态图中不包含回路，去掉最少的顶点的集合就是状态图的一个最小反馈点集.给定一个光纤网络，安装尽可能少的波长转换器，使得网络中的每一条路由所需要的波长数等于网络的拥塞界（用于安装波长转换器的顶点集合被称为充分集），拥塞界就是网络中经过任一条边的路的最大数目.此问题也等价于在所对应的有向图中求图的最小反馈点集问题.

因为确定一般网络（或图）的最小反馈点集问题属NP问题[1]，所以现阶段还不能对这一问题给出令人满意的结论.大多数的工作是在多项式时间内解决某些特殊图的反馈数问题，以及确定特殊图的最小反馈数的上下界.

文献[2]证明了一般图G＝（V，E）的反馈数的下界为

其中Δ＝Δ（G）为图G的最大度.这个下界给出了一般图G＝（V，E）的反馈数与图的最大度的关系.

大网络的构造通常是利用小网络的笛卡儿乘积方法构造而得到[3].由笛卡儿乘积方法构造出来的网络保留小网络的诸多优点，比如正则性、Euler性、Hamilton性、点可迁性等性质.超立方体网络是一类著名的互连网络拓扑结构.n维超立方体（n－dimensional hypercube），记为Qn，是由n个K2的笛卡儿乘积K2×K2×…×K2构造而得.

对于超立方体以及超立方体的变形网络（如交叉立方体、局部扭立方体、增广立方体）的最小反馈点集问题的结论目前还比较少，Focardi等[4]给出了超立方体Qn的反馈数的渐进界为.王彦辉等[5]给出了折叠超立方体Qfn的反馈数的渐进界为等[6]研究了有向图的反馈点集问题；文献[7～9]对网格图和置换图的反馈点集问题进行了研究.文献[10～13]给出 了 Directed split－stars、Kautz digraphs、Shuffle－based interconnection networks 等 著 名的网络拓扑结构图的反馈数的较好的上界.Xu等[14～16]对与线图相关的网络拓扑结构图，如de Bruijn有向图和de Bruijn无向图的反馈数进行了研究，得到了较好的反馈数的渐进界.

本文通过构造剩余子图G[V（Qfn）－F]的极大无圈子图得到极小反馈点集，从而得到反馈数的上界的方法，来研究折叠超立方体网络Qfn的反馈数问题.

1 定义和引理

n维折叠超立方体网络Qfn的概念是El－Amawy等[17]提出的.Qfn的顶点集合为

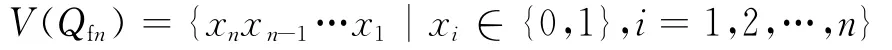
顶点x＝x n x n－1…x1与y＝y ny n－1…y1有边相 连 当 且 仅 当y＝y ny n－1…y1＝x n x n－1…x i＋1珚x ix i－1…x1，1≤i≤n（此时（x，y）称为正常边）或者y＝y ny n－1…y1＝珚x n珚x n－1…珚x1（此时（x，y）称为补边），顶点y称为顶点x的补点.

由此可见，n维折叠超立方体网络是超立方体变形网络，其通过在n维超立方体网络Q n中添加2n－1条补边构造生成，如图1所示.

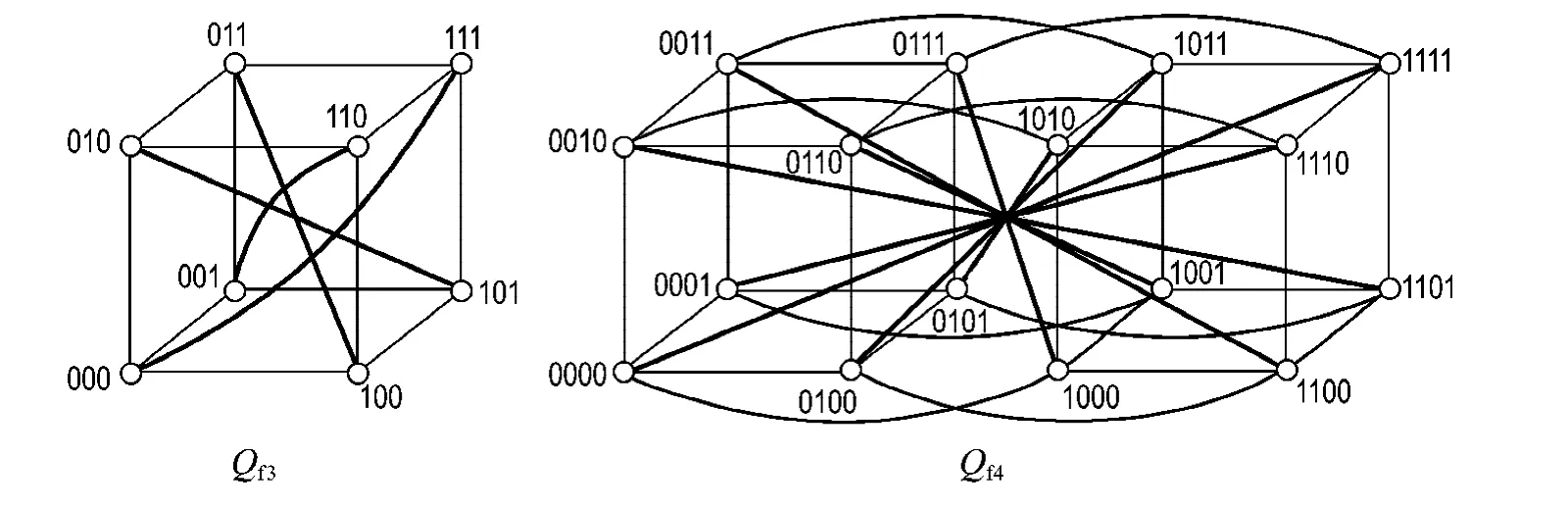
图1 折叠超立方体Q f3和Q f4Fig.1 Folded hypercube Q f3 and Q f4

由于Qfn具有下述优良的性质，被认为是替代超立方体Qn的挑战性网络结构.

（1）Qfn有2n个顶点，（n＋1）2n－1条边，且是n＋1正则图；

（2）Qfn直径为

（3）Qfn的连通度为n＋1；

（4）Qfn是点可迁图和边可迁图，因而是Cayley图；

（5）当n为奇数时Qfn是二部分图，当n为偶数时，Qfn是非二部分图.

定义1 给定n维折叠超立方体Qfn的顶点，若则称x为偶顶点；若，则称x为奇顶点.

设为折叠超立方体Qfn中所有奇顶点构成的集合，为折叠超立方体Qfn中所有偶顶点构成的集合，则Qfon和Qfen是Qfn的顶点集合的一个划分，故V（Qfn）＝Qfon∪Qfen.

定义2 给定超立方体Qn的两个顶点x和y， 设x＝xnxn－1…x1，y＝ynyn－1…y1， 称为两个顶点x和y之间的Hamming距离.

定义3 设S为超立方体Qn顶点子集，若对于任意顶点x，y∈S，均有DH（x，y）大于k（k为自然数），则称S为超立方体Qn的k分离集.

引理1[4]对任何整数n≥2，超立方体Qn中含有一个4分离集.设这个4分离点集合为R，R至少由2n－2/（n－1）个偶顶点组成，则R和Qn中所有的奇顶点的并导出的子图不含圈.

定义4 对于点集Q每个元素后面加上数串b形成的点集记为Qb.

例如R0为二进制编码点集合R的基础上后面加0形成的点集合，为二进制编码点集合Qn的基础上后面加00的点集合.

为中所有奇顶点的集合，为偶顶点集合.显然R0、、中的顶点的长度是n＋1.

2 折叠超立方体的反馈数的上界

由于当n为奇数时，n维折叠超立方体Qfn是二部分图，然而当n为偶数时n维折叠超立方体Qfn是非二部分图，下面分别讨论折叠超立方体的反馈数的上界.

2.1 折叠超立方体的阶为奇数的情况

定理1 当n为奇数时，折叠超立方体Qfn＋2中由顶点子集合导出的子图不含圈.

证明 因为n为奇数，n＋2也为奇数，故Qfn＋2是二部分图.又因为Qfn＋2中的奇顶点集合Qfon＋2及偶顶点集合Qfen＋2各为一半且各自为Qfn＋2的独立集，所以任意两个偶顶点之间没有边关联，任意两个奇顶点之间也没有边关联.

因为内都为奇顶点且是独立集，所以Q00fon内部任意两个顶点之间均没有边关联.

现在讨论与之间的关系.

由引理1知R00∪Q00fon导出的子图不含圈，且最后一位都为00，所以R00∪Q00fon导出的子图的边均为正常边.

（2）与以及与的关系

由定义4可知是由Qfon后加00组成的集合，而是由Qfen后加01组成的集合，所以之间有正常边，且为一一对应的，没有补边.

换句话说对于任意一个属于Qfon的字串α∈Qfon，有，则α00与α01、α10两个顶点相关联，均为正常边，故不含圈.

同理，对于任意一点α∈Q11fen，其补点珔α必然在Q00fon中，则Q00fon与Q11fen构成了一个双射函数.即之间有2n条补边包含且只包含一个中的点.

R00Q01Q10Q11Q00导出的子图不含圈.

定理2 对任意n≥4的奇数，Qfn的反馈数的上界为f（n）≤2n－1（1－1/8（n－3））.

Q11fen∪Q00fon在n＋2维折叠超立方体Qfn＋2导出的子图不含圈，因此

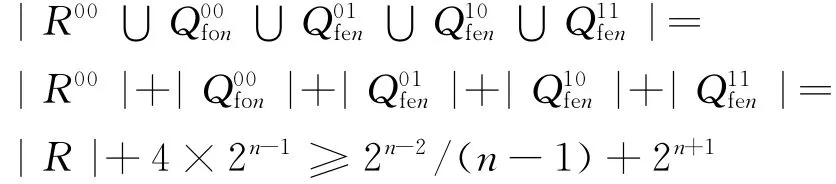
所以n＋2维折叠超立方体Qfn＋2的反馈数的上界为f（n＋2）≤｜Qfn＋2｜－

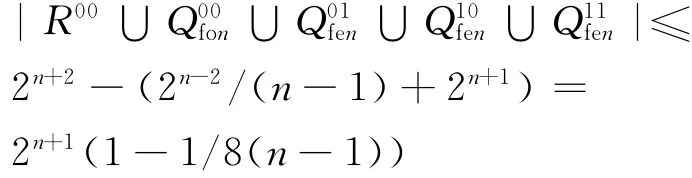
即n维折叠超立方体Qfn的反馈数的上界为f（n）≤2n－1（1－1/8（n－3））.

2.2 折叠超立方体的阶为偶数的情况

定理3 当n为奇数时，Qfn＋3是偶阶的，由Qfn＋3中的点R000∪Qfon＋3导出的子图不含圈.

证明 分正常边和补边两种情况进行讨论.

（1）R000∪Qfon＋3的补边

当n为奇数时，n＋3是偶数，一个点和其补点是同奇偶的，所以R000和Qfon＋3之间没有补边.R000后三位均为000，故其内部点之间没有补边.

又因为Qfon＋3为Qfn＋3的全部奇顶点，所以由定义可知Qfon＋3内部有2n＋1条补边.将Qfon＋3按照后三位进行子集合分解可以得到8个子集的并集如下：

于是Q000fon的补点在Q111fon中，则Q000fon与Q111fon之间有2n－1条补边，且Q000fon中的点与Q111fon中的补点是一一对应的.

同理Q001fon与Q110fon、Q010fon与Q101fon、Q011fon与Q100fon之间具有相同的性质.

（2）R000∪Qfon＋3的正常边

因为折叠超立方体中正常边的两条边不能同奇偶，显然R000内部没有正常边，Qfon＋3内部也不包含正常边.所以只需计算R000和Qfon＋3之间的正常边即可.

由引理1可得，R000∪Q000fon构成一个无圈子图.

因为对于任意一个R中的元素α∈R，在α后加子串000形成R000，而在α后分别加子串001、010、100形成3个点集，分别为Q001fon、Q010fon、Q100fon的子集，则R000与Q001fon、Q010fon、Q100fon的子集有连边且为一一对应关系.又因为Q000fon、Q001fon、Q010fon、Q100fon之间没有补边相关联，即没有任何边，所以由R000∪Q000fon∪Q001fon∪Q010fon∪Q100fon导出的子图为无圈子图.

综上，构成的R000∪Qfon＋3在Qfn＋3导出的子图为无圈子图.

定理4 对任意n≥4的偶数，Qfn的反馈数的上界为f（n）≤2n－1（1－1/16（n－4））.

证明 由定理3可知，R000∪Qfon＋3在Qfn＋3导出的子图不含圈，故得到

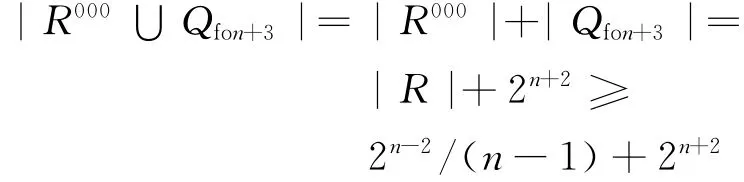
所以n＋3维折叠超立方体Qfn＋3的反馈数的上界为

所以n维折叠超立方体Qfn的反馈数的上界为

3 无圈导出子图的连通性分析

定理5 如果n为奇数，则构造的Qfn＋2的无圈导出子图的连通分支个数和Qn的无圈子图R∪Qfon中连通分支个数一致.

证明 设H＝G[R00∪Q01fen∪Q10fen∪Q11fen∪Q00fon]，考虑无圈导出子图H的边的情况.实际上，H的边是在R∪Qfon边的基础上增加与Q01fen∪Q10fen∪Q11fen的点之间的边，也即，在R∪Qfon基础上，增加Q01fen∪Q10fen∪Q11fen这些点，并没有增加实际的连通分支.

定理5表明，当n为奇数时，构造的Qfn＋2的无圈导出子图的整体连通性能与引理1中构造的Qn中不含圈导出子图R∪Qfon的是一致的，但由于阶数大了两阶，连通性能比同类其他反馈集变得更优.

4 结 语

反馈数问题是图论和网络理论极难的问题之一，文献中有关此研究领域的结果不多，关键是还没有找到一个好的方法来处理这个问题.本文所讨论的n维折叠超立方体在n为奇数和偶数时分别是二部分图和非二部分图，根据此性质，本文对于n为奇数和偶数两个大类的情况分别构造了n维折叠超立方体的无圈导出子图，给出了折叠超立方体网络的反馈数的新的上界，改进了已有的结果.

[1]GAREY M R，JOHNSON D S.Computers and Intractability[M].San Francisco：Freeman，1979

[2]BEINEK L W，VANDELL R C.Decycling graphs[J].Journal of Graph Theory，1997，25（1）：59－77

[3]XU Jun－ming.Topological Structure and Analysis of Interconnection Networks [M].London：Kluwer Academic Publishers，2001

[4]FOCARDI R，LUCCIO F L，PELEG D.Feedback vertex set in hypercubes[J].Information Processing Letters，2000，76（1－2）：1－5

[5]王彦辉，徐俊明.折叠超立方体网络的最小反馈点集[J].运筹与管理，2005，14（6）：8－11

[6]SMITH G W JR， WALFORD R B. The identification of a minimal feedback vertex set of a directed graph[J].IEEE Transaction on Circuits and Systems，1975，CAS－11（1）：9－15

[7]BAU S，BEINEKE L W，LIU Z.etal.Decycling cubes and grids [J].Utilitas Mathematica，2001，59：129－137

[8]LIANG Y D.On the feedback vertex set problem in permutation graphs [J].Information Processing Letters，1994，52（3）：123－129

[9]LUCCIO F L.Almost exact minimum feedback vertex set in meshes and butterflies[J].Information Processing Letters，1998，66（2）：59－64

[10]WANG C C，LLOYD E L，SOFFA M L.Feedback vertex sets and cyclically reducible graphs [J].Journal of the ACM，1985，32（2）：296－313

[11]WANG Fu－hsing，HSU Cheng－ju，TSAI Jen－chih.Minimal feedback vertex sets in directed split－stars[J].Networks，2005，45（4）：218－223

[12]KRLOVIC R，RUZICKA P.Minimum feedback vertex sets in shuffle－based interconnection networks[J].Information Processing Letters，2003，86（4）：191－196

[13]XU Jun－ming，WU Ye－zhou，HUANG Jia，etal.Feedback numbers of Kautz digraphs[J].Discrete Mathematics，2007，307（13）：1589－1599

[14]XU Xi－rong，CAO Yong－chang，XU Jun－ming，etal.Feedback numbers of de Bruijn digraphs[J].Computer and Mathematics with Applications，2010，59（2）：716－723

[15]XU Xi－rong， YANG Yuan－sheng， MING Di.Feedback vertex set of generalized de Bruijn digraphsGB（d，n）[J].Utilitas Mathematica，2009，79：107－124

[16]XU Xi－rong，XU Jun－ming，CAO Yong－chang.Bounds on feedback numbers of de Bruijn graphs[J].Taiwanese Journal of Mathematics，2011，15（3）：1101－1113

[17]EL－AMAWY A， LATIFI S. Properties and performance of folded hypercubes [J].IEEE Transaction on Parallel and Distributed Systems，1991，2（1）：31－42