一种波导高通滤波器的优化设计

沈显照 王群杰 肯 诺

(中国电子科技集团公司第38研究所 合肥 230031)

1 引言

为了使无线电发射设备寄生输出控制在一定范围之内，在馈线系统中增加大功率波导微波滤波器是减小寄生输出的一种有效方法，本文介绍了一种S波段波导高通滤波器的设计方法及其设计实例。

滤波器[1]作用为允许所需要频率信号以最小可能的衰减通过，同时衰减不需要的频率信号。随着微波技术的迅猛发展，波导型滤波器的需求越来越大、使用范围越来越广，当然也对其性能提出越来越高的要求。利用电磁场商业软件固然可以用于电磁工程设计，然仿真计算过程非常繁杂，效率低，不利于工程设计。若结合等效电路进行预先参数提取，则可大大加速设计过程。为了获取等效电路的参数，常需优化。遗传优化等算法[2]在电磁工程中的应用已十分普遍。本文采用一种全新的全局优化算法，即粒子群优化算法(Particle Swarm Optimization)[3]，而该算法可调参数少，简单、易于实现并且功能强大，在目标优化、模式识别、调度、信号处理、决策控制等多方面广泛应用。

2 设计原理[4]

波导高通滤波器是利用矩形波导本身低频截止，高频无耗传输的特性，按照阻抗匹配的原理，通过改变各节波导段的阻抗值，从而设计出符合性能指标要求的高通滤波器。通常改变波导的宽边尺寸，以满足其耐功率性能。

图1给出了典型的阻抗匹配器的电路图。利用二端口网络理论[5]可求得总的转移矩阵[A]，则可

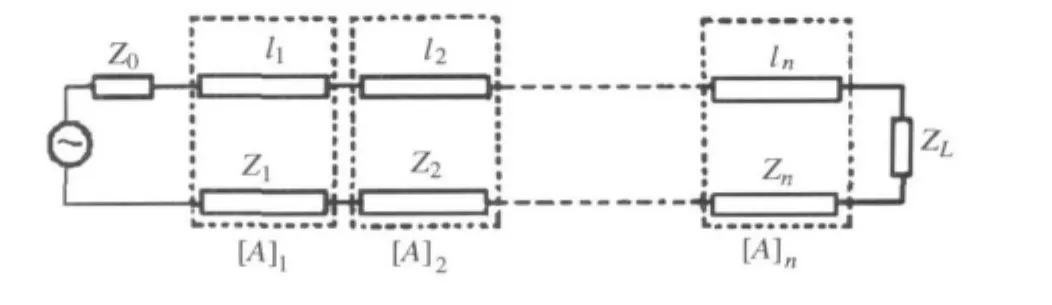
图1 阻抗匹配器的电路图

求得输入侧的参数。

输入阻抗

其中:

输入电压反射系数

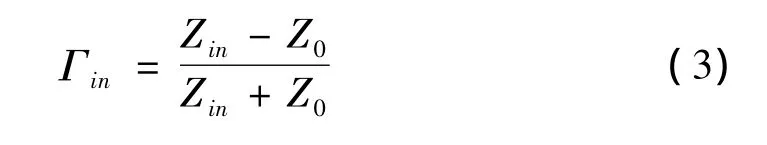
电压驻波比

从上面的公式以及[A]距阵和[S]距阵之间的转换关系，可以得出电压驻波比VSWR、S21和Zi之间的关系。因要求通带VSWR≤VSWRmax(某一给定值)以及阻带抑制S21≤S21max(某一给定值)，通过计算可以得出各节的初始阻抗值Zi。

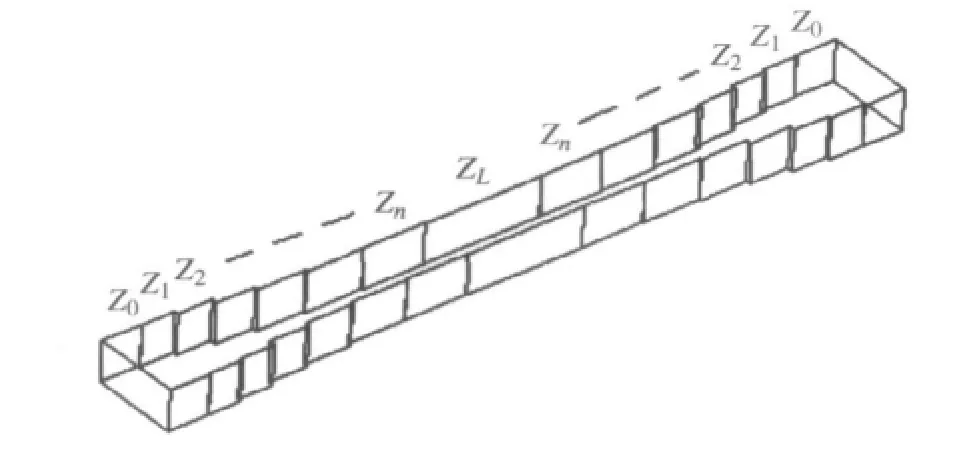
图2 波导高通滤波器的结构模型图

根据1/4波长阻抗变换器[5]的设计原理，可计算出各节变换段的电长度尺寸。

当频率低于波导截止频率时，波导的传播常数β不再是实数，而是虚数，此时波导中存在的是衰减波。其衰减常数为:

由上式可知，截止波导的宽边越小，衰减越大;频率越低，衰减越大。当然，截止波导段越长，带外衰减越快。因此进行结构紧凑设计时，我们应同时兼顾通带匹配和带外衰减。

3 优化设计

为进一步优化求解1/4波长阻抗变换段的阻抗值，采用了结构简单、通用有效且运行快的粒子群优化算法，很好地求解了波导高通滤波器的各节1/4波长阻抗变换段的阻抗值，得出各节的归一化特性阻抗值和实际长度。

粒子群算法首先初始化一群随机粒子，然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个“极值”来更新自己。一个是粒子本身找到的最优解，即个体极值。另一个是整个种群目前找到的最优解，称之为全局极值，粒子在找到上述两个极值后，就根据下面两个公式来更新自己的速度与位置:

其中，V是粒子的速度;present是粒子的当前位置;rand是0～1之间的随机数;c1、c2为学习因子。通常，c1=c2=2。w是加权系数，取值在0.1～0.9之间。

实验证明，如果w随算法迭代的进行而线性减小，将显著改善算法的收敛性能。设wmax为最大加权系数，wmin为最小加权系数，iter为当前迭代次数，iter－m为算法的总迭代次数，则有:

本文选择通带驻波以及阻带抑制作为优化的目标，两者按照一定的比例权重相加。以优化得到的通带驻波值与给定值S11max(即VSWRmax)的差值的绝对值作为A;以优化得到阻带抑制与给定值S21max的差值的绝对作为B，两者按照一定的比例权重相加作为适应度函数。此值越靠近0，表明优化的效果越好，此时得出的Zi和对应的长度即为所要求的波导高通滤波器各波导段的参数。

4 设计实例

通过粒子群优化算法优化波导高通滤波器各节的归一化特性阻抗，我们设计了n=7的S波段波导高通滤波器。在Matlab中通过PSO优化，最终得到的各节的归一化特性阻抗为和长度为图3描述了粒子群优化算法的框架。

n=7的波导高通滤波器的归一化阻抗值和1/4波长电尺寸数据如下。

图3 PSO程序框图

图4为粒子群优化算法优化的收敛曲线，图5为ANSOFT HFSS软件仿真计算结果与优化结果的比较图，通过此图表明两者的曲线吻合的很好，从而证明了PSO优化的可行性和有效性。

按照上述粒子群算法的优化结果，设计制作了S波段的波导高通滤波器，其实物图见图6。

图6 S波段波导高通滤波器实物图

该波导高通滤波器的实测结果为:通带损耗≤0.14dB、带外(1.1 GHz～2GHz)抑制≥64dB、通带驻波VSWR≤1.04。其中:图7为滤波器带内损耗的实测结果，图8为滤波器带外抑制实测结果，图9为滤波器的带内驻波实测结果，图10为滤波器宽频带S21幅度的实测结果。

通过S波段的波导高通滤波器的仿真计算及优化结果(图4)和实测结果(图9、图10)的比较，可看出，优化结果与实测结果是非常一致的，这说明等效电路模型是非常准确和有效的，优化结果是可信的。

5 结论

在粒子群优化算法的基础上实现了对波导高通滤波器的综合优化设计。不仅简化了波导高通滤波器的设计过程，还实现了高性能要求，该方法具有较高的工程应用价值。

[1]范立，一种新型超宽带带通滤波器的设计[J].火控雷达技术，2010，(4).

[2]张昭阳，任意位置稀布阵天线的遗传优化[J].火控雷达技术，2009，(3).

[3]J Kennedy，R C Eberhart.Particle swarm optimization[C].IEEE International Conference on Neural Networks，Perth，Australia，1995.

[4]甘本袚，吴万春.现代微波滤波器的结构与设计[M].北京:科学出版社，1972.

[5]Microwave Solid State Circuit Design[M].北京:电子工业出版社，2006.