一种深度欠采样的快速SAR成像算法

王 健 宗竹林

(电子科技大学 成都 611731)

1 引言

合成孔径雷达能够全天时、全天候对远距离目标进行二维高分辨成像，具有广泛的应用。随着应用的不断深入，人们对成像的质量，如图像的分辨率，可判读性及视觉效果，都提出了更高的要求。传统的成像算法是基于奈奎斯特采样定理，由于SAR回波原始数据量非常大，给数据的传输和存储带来很大困难[1，2]。

CS理论是由Donoho等人从信号稀疏分解和逼近理论进一步发展的一种新的信号处理理论，它彻底改变了人们对信息获取的传统观念，由于突破了奈奎斯特采样定理的限制，该理论一经提出，就在信号/图像处理、医疗成像、模式识别、地质勘探、光学/雷达成像、无线通信等领域受到高度关注，并被美国科技评论评为2007年度十大科技进展[3]。CS在雷达领域的应用也得以迅速展开。文献[4]首次提出了随机滤波的信号处理方法，实现了基于CS的SAR成像;文献[5]采用Alltop sequence作为雷达发射信号，构造了一个冗余字典，并在模糊域上实现了高分辨率雷达成像，突破了最大不模糊距离的限制。此外许多国内研究者[6～9]也在CS雷达成像上取得了一些研究成果。

目前CS在雷达成像上的研究主要集中在距离向或方位向的一维压缩感知成像，这些算法需要利用一个完整的合成孔径时间内的回波数据才能实现二维成像。本文以进一步减少SAR成像所需数据量，缩短成像时间为目的，提出了一种深度欠采样的压缩感知成像算法，并在此基础上利用OMP和BCS算法对压缩后的数据恢复重构，实现了雷达二维成像。由于该算法所需的回波数据小于一个合成孔径时间内的回波数据，从而等效的减小数据获取时间，加快了成像速度。

2 压缩感知基本理论

CS是建立在信号稀疏表示基础上的信号采样理论。该理论指出，任意N维K稀疏信号的稀疏表示X可以通过在RN空间的M=O(K·log(N/K))，(M≪N)维随机测量值y以很高的概率精确重构。

假设一个离散信号 X=(x1，x2，…，xN)，长度为N，如果信号X是稀疏的或可压缩的，则存在一组稀疏基 Ψ =[Ψ1，Ψ2，…，ΨN]使得X可以表示为:

其中Ψ是一个N×N的稀疏矩阵，σ是N×1的稀疏系数，包含K个非零值。

随机测量过程是将信号X投影到一组测量矩阵Φ上，使测量对象从N维降为M维，从而得到测量值。随机测量过程的数学表示为:

式中y表示M维随机测量值，Φ为M×N维测量矩阵，ne为零均值高斯白噪声。

当矩阵θ满足RIP准则[10]时，就可以运用压缩感知重构算法恢复信号X。

2.1 BCS[12] 算法

y的似然函数为:

使用最大似然法求上式的X会导致过学习。为避免这种情况，对权值X赋予先验的条件概率分布:

其中α =[α1，…，αN]T是一个控制权值先验方差的N维向量。如果能求得α，就很容易得到X。α可通过最小化下面的代价函数而得到。

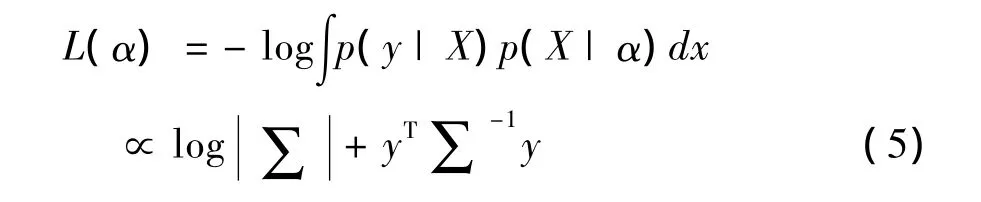
使用EM算法求解上式，得到的第(k+1)步的迭代公式如下:

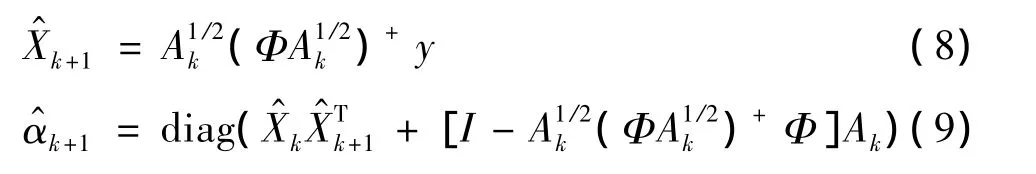
2.2 OMP[11]算法流程

A.初始化测量次数，初始化残差:r=y;

B.利用最小二乘法找到与y相似最高的θ的列即内积最大的列，最小二乘法步骤如下:

a.将θ的每一列代入＜rH，θi＞，找到使内积＜rH，θi＞ 最大的一列记为 θq1;

b.A=θq1，并将对应的 θ的第 i列置零，θ(:，i)=0;

C.返回(2)进行下一次迭代，此时 A={θq2，θq1};

D.迭代终止。其中 A=diag(α0，…，αN)。对于稀疏信号表示的问题，以上迭代算法可写成:

3 基于压缩感知的SAR成像

3.1 深度欠采样回波信号模型

图1中给出了正侧视模式下SAR平台的几何模型，X轴表示方位向，Y轴表示平台速度方向，Z轴为高度向。

图1 正侧视SAR几何关系

雷达以速度V沿y轴方向匀速运动，在一个合成孔径时间内，连续发射线性调频脉冲信号:

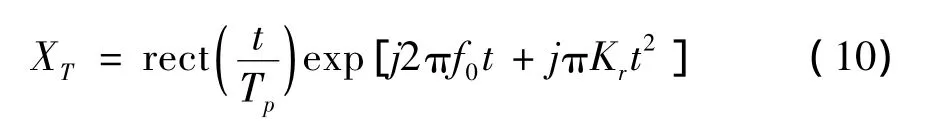
在慢时间τ=m×PRT时刻，雷达平台至点目标k的距离可表示为rk(τ)，雷达系统接收到的回波信号可以描述为:

其中σk为散射点k的后向散射系数;f0为载频;c为光速;Tp为线性调频脉冲信号的时间宽度。

根据CS可以完成不完全数据重构的思想，本文利用前1/2个合成孔径时间内的数据来获取测量信号，这样缩短了数据获取的时间，加快了成像的速度。

图2 回波采样示意图

图2表示RD算法和CS算法对回波数据采样的示意图，“■”表示采样点，“□”表示非采样点。图2(b)表示对一个合成孔径时间内的接收到的前50%的数据采样，并且选择随机高斯矩阵[13]作为测量矩阵。测量过程如下:

其中Φ是M×N维随机高斯矩阵，即随机选择N维信号X中的M维，从而得到欠采样信号y。随机测量矩阵可以表示为:

Φ中“1”表示随机测量数据，“0”表示丢弃的数据，CS算法即由对应于Φ中“1”的测量数据重构出原始信号的过程。

3.2 基于压缩感知的SAR成像

假设雷达平台在一个合成孔径时间内扫描的二维场景为ξ，将二维场景区域均匀离散成Na×Nr个点散色目标，将Na×Nr个点目标回波延迟按行展开，构成一个一维向量，长度为N=Na×Nr，N个点目标的坐标可以表示为 β =(β1，β2，…，βN)，其中 βi=(xi，yi，zi)是点目标i的坐标向量，对应的散色系数可以表示为 σ =(σ1，σ2，…，σN)，为保证信号的稀疏性，假设只有少数的K个散色系数是非零的，即:

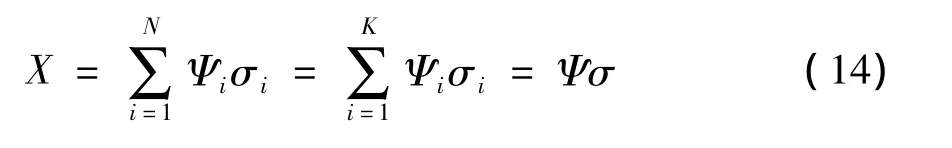
根据(11)式和(14)式，可以得知对于N个点目标β =(β1，β2，…，βN)，在Ψ变换域下可以实现对雷达回波的稀疏表示。对于每个点目标，变换域Ψ可以表示为 Ψ =(φ1，φ2，…，φN)，其中点目标 βi对应于变换基φi，按行展开得到N×1的向量，表示为:

式中，Ri是点目标i与平台间的斜距;yi是点目标i在y轴方向与点目标之间的距离;Lsar为合成孔径长度。

将上述变换基和(13)式代入(12)式，便可得到测量信号，由于随机采样在实现过程较为复杂，在实际中可以采用等间隔采样来取代随机高斯测量，在硬件实现上可以用低速率AD对回波数据采样获得测量信号。综上所述，CS雷达成像处理流程可以用图3描述。

图3 CS雷达成像框架

图3中的A/D是以较低的采样率对雷达回波信号采样，得到M×1欠采样测量信号y=(y1，y2，…，yM)，这样在得到了传感矩阵和测量信号后，就可以用压缩感知重构算法对回波信号做脉冲压缩。脉冲压缩过程即(12)式中获取测量信号的逆过程，通过测量信号y和传感矩阵θ=ΦΨ得到散色系数σ。

本文在 CS脉冲压缩过程采用 OMP[11]和BCS[12]两种算法实现。OMP算法利用上述传感矩阵θ=ΦΨ和测量信号y可以实现对欠采样回波的脉冲压缩。BCS算法需要对θ=ΦΨ和y做如下变换来得到传感矩阵和测量信号。

上式将测量信号的实部虚部分开来获取实测量信号 yr。

对应的变换域是对Ψ中的φi做如下变换。

从 而 得 到 BCS 的 变 换 域 Ψr= (φr1，φr2，…，φrN)。

将(13)式中测量矩阵扩展为2M×2N维，得到BCS算法随机测量矩阵Φr，利用BCS算法做脉冲压缩的过程表示如下:

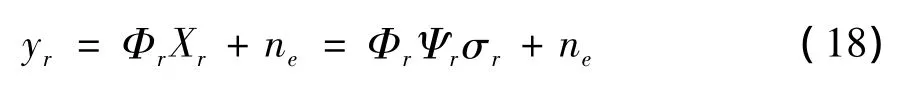
图3中后处理过程即将得到的一维散色系数转化为二维图像的过程，OMP和BCS算法的后处理过程可以表示如下:

4 仿真结果

假设雷达工作在正侧视模式下，场景中心到载机航线的垂直距离Rb=2000m，距离向欠采样率和方位向欠采样率分别为Dr和Da，距离分辨率和方位分辨率为1m，仿真中用到的雷达参数有:

信号带宽:150MHz 采样率:200MHz

脉冲宽度:0.5μs 脉冲重复频率:500Hz

载机速度:150m/s 载频:10GHz

图4 重构误差与方位向降采样率

本文首先分析了在距离向降采样率Dr=1/5，方位向降采样率与重构误差的关系，在15个点目标的场景区域，仿真结果如图4所示。

由图4可以看出，在图中降采样率情况下重构误差可以满足精确重构的要求，所以在后面的仿真中选用方位向将采样率Da=1/2，即半个合成孔径时间的数据。

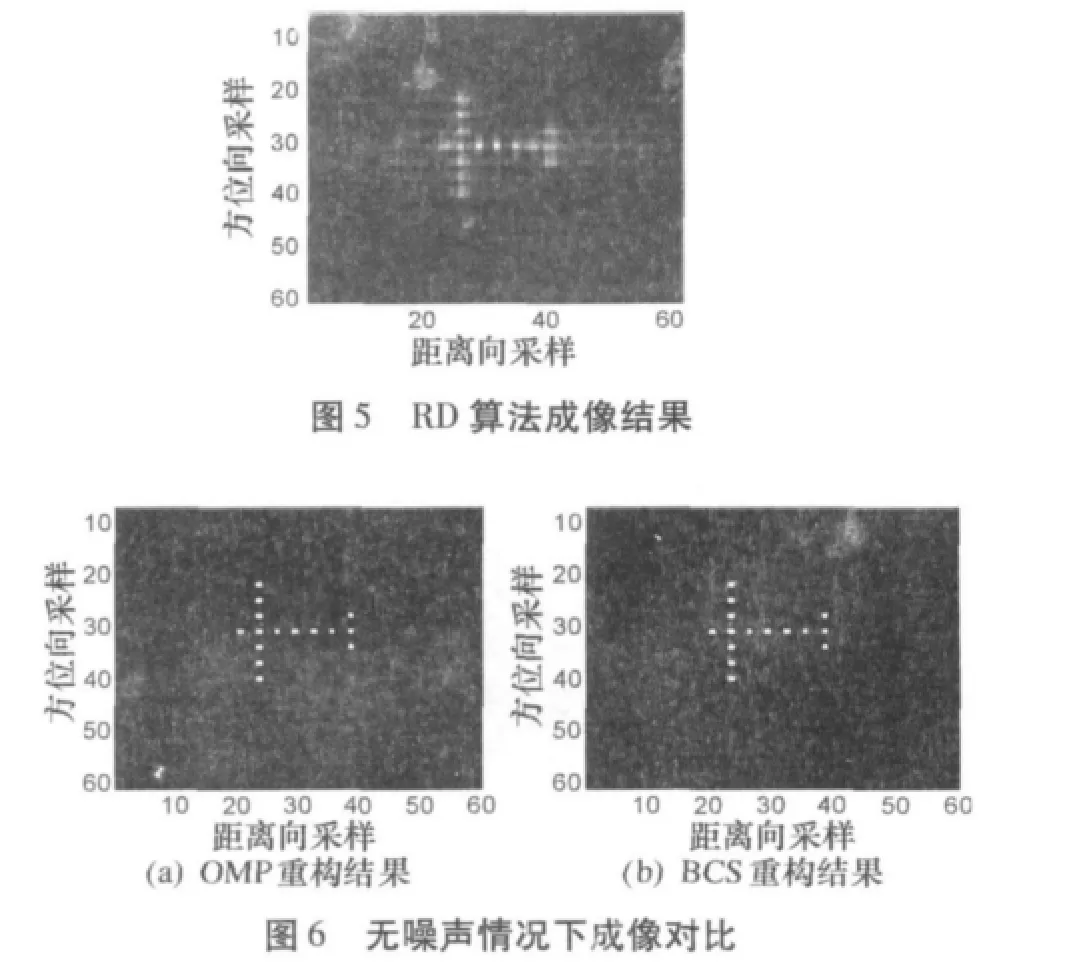
图5中显示的是在无噪声情况下传统的RD算法成像结果。图6为无噪声情况下压缩感知算法重构的目标场景区域，其中图6(a)是由OMP算法得到的成像结果，图6(b)是BCS算法的重构结果。可以看出CS算法在无噪声情况下可以完美的重建图像信息。

由于信噪比大小对RD算法成像的影响是我们所熟悉的，下面是在SNR不同情况下的仿真给出CS方法成像的结果，对应的RD算法成像效果与图5并无明显区别。

图7 SNR=5dB情况的成像结果

图7是在信噪比SNR=5dB情况下，对目标空间的重构结果。图7(a)和图7(b)分别是OMP算法和BCS算法的重构结果，从图中可以看出，出现了一些能量较弱的“假目标”。

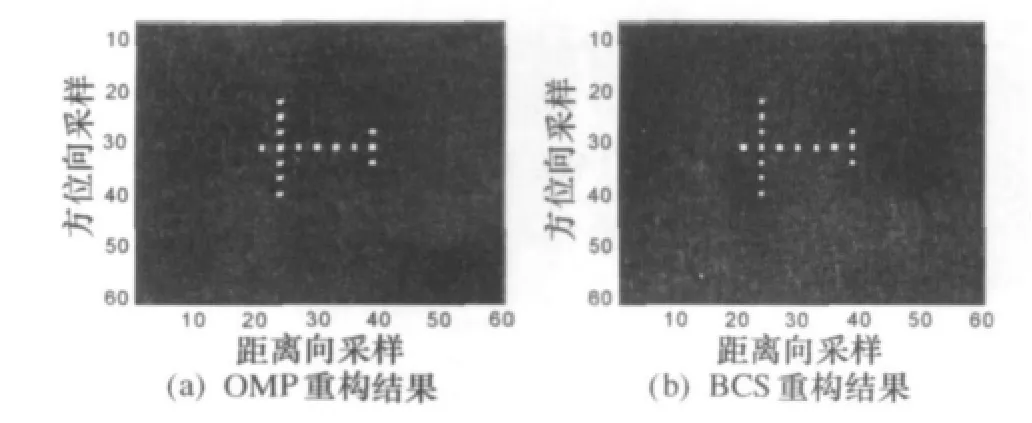
图8 SNR=25dB情况的成像结果

图8是在SNR=25dB情况下，OMP算法和BCS算法重构的二维场景，可以看出在25dB时，噪声对重构结果的影响很小，场景区域得到了正确的重建。

图9和图10是RD算法与CS算法在单个点目标下的三维图像，与图5和图6二维图相对应。

通常方位向采样数据的减少会直接降低方位向分辨率，由图6和图10与图5图9对比可知，本文提出的CS算法在降低方位向采样数据的情况下，不仅没有降低方位向的分辨率，并且该算法消除了目标旁瓣，提高了成像分辨率。

对上述信噪比不同情况下，OMP算法和BCS算法的重构结果进行定量的分析，通过重构误差、重构时间、重构信号的LSNR几个参量对重构图像进行评估。其中重构误差定义为:

定义重构信号的局部信噪比为LSNR[7]，用来反映图像的重构效果，计算公式如下:

通过对不同SNR条件下重构误差的计算，得到图11所示的曲线，可以看出，BCS和OMP算法的重构误差随着输入信噪比的增大，逐渐减少，并且逐渐趋近于零。

图11 重构误差与SNR的关系

在重构的过程中统计重构所需时间，得到图12中重构时间与SNR的关系，重构时间随着信噪比的增大逐渐减少，在30dB之后逐渐趋于稳定。由图12可以看出信噪比的大小对重构时间有较大的影响。

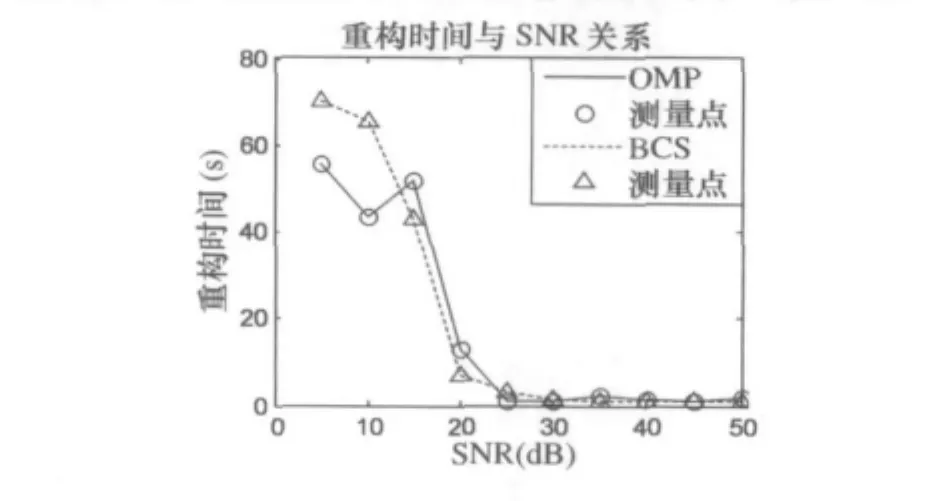
图12 重构时间与SNR的关系

图13表示了重构信号局部SNR和输入信号SNR的关系，LSNR与输入信号SNR成正比，并随着输入SNR增大而增大。图13中的曲线表明，随着输入SNR的增大，重构图像的效果就越好。由此可知，图11与图13的定量分析与上述成像的视觉效果相吻合。

图13 LSNR与SNR的关系

由以上仿真结果可以看出，在一个合成孔径时间内，传统的RD成像方法扫描的数据量为Na×Nr，CS方法仅使用了Na/2×Nr/5的数据量，大幅度的降低了数据量，同时仿真仅用了一个合成孔径时间内的前50%的数据，这等效于在1/2个合成孔径时间内获得的数据，因此缩短了数据获取时间，实现了快速成像。与传统SAR成像相比，CS成像算法消除了目标旁瓣，提高了成像的分辨率，并且有效的降低了成像系统的数据率。

5 结论

本文提出了一种深度欠采样快速SAR成像算法，在小于一个合成孔径时间里获得的数据进行测量，获取欠采样回波数据，然后利用CS脉冲压缩算法重构，实现了快速高分辨雷达二维成像。该算法能够有效地降低高分辨率雷达成像系统的数据率，减少硬件系统(特别是A/D转换器)的实现难度，消除了目标旁瓣，提高了成像的分辨率，同时缩短了成像时间。

[1]Sujit Bhattacharya，Thomas Blumensath，Bernard Mulgrew，et al.Fast encoding of synthetic aperture radar raw data using compressed sensing[J].IEEE Workshop on Statistical Signal Processing，2007:448－452.

[2]Gabriel Rilling，Mike davies and bernard mulgrew.Compressed sensing based compression of SAR raw data[C].Singnal Processing with A-daptive Sparse Structured Representations Workshop，Saint-Malo，France，2009.

[3]喻玲娟，谢晓春.压缩感知理论简介[J].数字视频，2008，32(12):16 －15.

[4]Baraniuk R and Steeghs P.Compressive radar imaging[C].IEEE Radar Conference，Boston，MA，USA，Apr.17－20，2007:128－133.

[5]Herman M and Strohmer T.Compressed sensing radar[C].IEEE International Conference on A-coustics，Speech and Signal Processing，Las Vegas，NV，USA，Mar.30 － Apr.4，2008:1509－1512.

[6]谢晓春，张云华.基于压缩感知的二位雷达成像算法[J].电子与信息学报，2010，32(5):1234－1238.

[7]谢晓春.压缩感知理论在雷达成像中的应用研究[D].中国科学院空间科学与应用研究中心，2010.

[8]Lei Zhang，Meng-dao Xing，Cheng-Wei Qiu，Jun Li，Jia-lian Sheng，Ya-chao Li，Zheng Bao.Resolution enhancement for inversed synthetic aperture radar imaging under low SNR via improved compressive sensing[J]，IEEE transactions on geosciences and remote sensing，2010，48(10):3824 －3838.

[9]Hongxian Wang，Yinghui Quan，Mengdao Xing，and Shouhong Zhang.ISAR imaging via sparse probing frequencies[J]，IEEE Transactions on Geosciences and Remote Sensing，2010，8(3):451－454.

[10]E Candès.The restricted isometry property and its implications for compressed sensing[J].Acadèmie des sciences，2006，346(I):598 －592.

[11]Tropp J A，Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit[J]..IEEE Transactions on Information Theory，2007，53(12):4655－4666.

[12]Ji S H，Xue Y，and Carin L.Bayesian compressive sensing[J].IEEE Transactions on Signal Processing，2008，56(6):2346 －2356.

[13]R Baraniuk.A lecture on compressive sensing[J].IEEE Signal Processing Magazine，2007，24(4):118－121.

[14]Sadegh Samadi，Müjdat Cetin，Mohammad Ali Masnadi-Shirazi.Sparse representation-based SAR imaging[J].IET Radar Sonar Nacig，2011，5(2):182 －193.