基于Matlab软件的伺服系统设计方法

高 栋 胡卫鹏

(西安电子工程研究所 西安 710100)

1 引言

传统的伺服系统设计建立在设计人员的工程经验和经典理论计算基础之上，缺乏系统的理论指导，往往在出现问题后不能对现有系统作出全面的分析从而发现问题的本质。此外，人工编写代码工作量大，且工作繁杂、易出错。因此，设计人员往往会选择较为简单的控制算法来完成伺服系统的设计工作，对于高性能要求的场合这种方法很难满足系统的指标要求。基于上述情况，如何将先进的现代控制理论与实际工程经验有机地结合起来，根据理论来指导工程设计，就成为现代伺服控制系统设计中面临的主要问题。

本文将Matlab软件中的各个组件，如Simulink、Parameter Estimation、Linear Analysys、SISO Tool、RTW Coder等有机地结合起来，从而形成一套从模型建立、参数辨识、系统仿真、控制器设计、产品级代码生成到效果验证的一系列完整的设计流程。

该设计方法不仅可以大大提高伺服系统的设计效率，使理论与工程实践紧密结合，而且可以更加便捷、有效地实现及验证各种类型的控制算法。

2 系统概述

本文研究的伺服系统为X－Y方向的二维系统，结构形式采用齿轮传动。系统采用典型的三环路控制结构，即电流环、速度环和位置环，其控制框图如图1下所示。

图1 控制系统原理框图

3 系统建模

3.1 电机模型的建立

本文选用永磁直流力矩电机，其模型可等效为电枢电阻和绕组电感的串联，即R－L串联结构。模型的建立主要参考二个重要的平衡方程，即电势平衡方程和转矩平衡方程。

其中，电势平衡方程为:

式中，Uq为电机电压;pn为磁极对数;ψr为磁链空间矢量;Rsiq为电枢压降;为电机绕组电压。

转矩平衡方程为:

式中，pn为磁极对数;ψr为磁链空间矢量;Td为负载转矩;J为转动惯量;p为微分算子。

将(1)、(2)进行拉普拉斯变换转化为方程组:

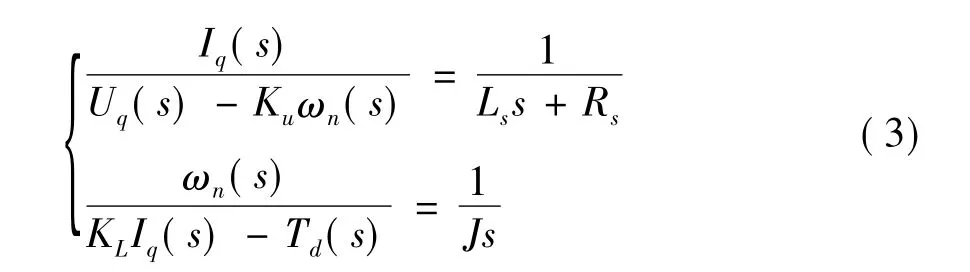
式中，Ku=KL=pnψr;Ku为电机的反感应电动势系数;KL为电机的转矩系数。

由该方程组可得电机的原理框图2。

图2 电机原理框图

根据该框图建立Simulink模型图3。

图3中，r为传动比;n为传动效率。考虑到控制信号饱和因素的影响，电机模型中增加饱和模块。

3.2 负载模型的建立

负载转矩折算到电机转轴上的转矩主要包括惯性力矩、干摩擦力矩和黏性摩擦力矩。由于本文采用齿轮传动，因此在建立负载模型时除了需要考虑上述因素外，还应考传动间隙和弹性形变的影响。其中，弹性形变的影响可以通过下述表达式给出:

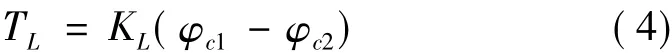
式中，KL为机构传动的弹性模量;φc1为电机轴的转角;φc2为负载轴的转角;TL为负载转矩。

式(4)计算出的负载转矩，除去干摩擦和黏性摩擦的消耗，最后转换为机构的惯性负载。根据上述理论可以建立起负载的Simulink模型，如图4所示。

在建立负载模型时，本文还考虑了齿轮传动间隙等非线性因素的影响。电机轴转角φd与系统输出轴转角φc之间的关系为:

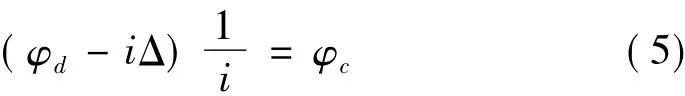
传动间隙的特性如图5所示，以电机轴为主动轴来表示，总间隙用2Δ表示，两边直线的斜率K相等，

图4 负载Simulink模型图

图5 机械间隙示意图

传动系统存在的间隙对伺服系统动、静态性能均有影响。为便于分析，将所有传动间隙集中在一处，并以执行电机轴为主动轴来进行分析。在Simulink中用DeadZone模块来模拟此间隙特性，并加在负载模型的角度输出端。

通过上述分析，最终将所有要考虑的负载力矩求和可得总的负载力矩，如下式:

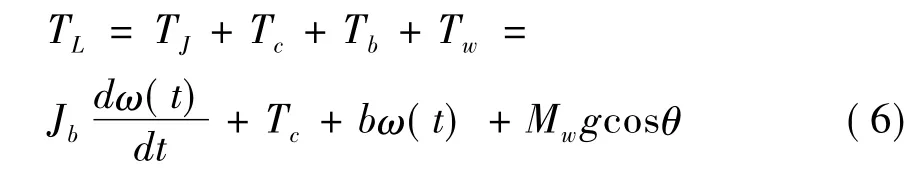
由于伺服系统中存在传动机构，因此在考虑传动比和传动效率后，得:

式中，i为传动比;η为传动效率。

3.3 传感器模型的建立

文中采用二维挠性陀螺来感知机构的旋转角速率，用电位计测量位置信息，用采样电阻求电机电流。在控制系统建模中，传感器的模型通常只考虑其量测误差。因此模型中利用随机信号针对测电流、测位置时的误差建立了相应的误差模型。而测角速度的挠性陀螺，需要考虑其二阶模型。利用陀螺自身所提供的阻尼比ξ、固有频率ω和标度因数n可以写出陀螺的传递函数模型:

4 模型参数辨识

通过上述理论分析，建立起电机和被控对象的模型。该模型的传递函数结构已经确定，但是某些关键参数还不准确。为了得到更加准确的模型，对被测平台进行PWM占空比测试。在不同的PWM占空比下，测试出机构的输出电流，转角和转速。通过分析试验数据，采用转速曲线对动摩擦系数、干摩擦力矩、电机的反电动势系数、电机的转矩系数以及传动轴的弹性模量这五个参数进行辨识。图6为实测的电机输出电压和机构转速的曲线图。

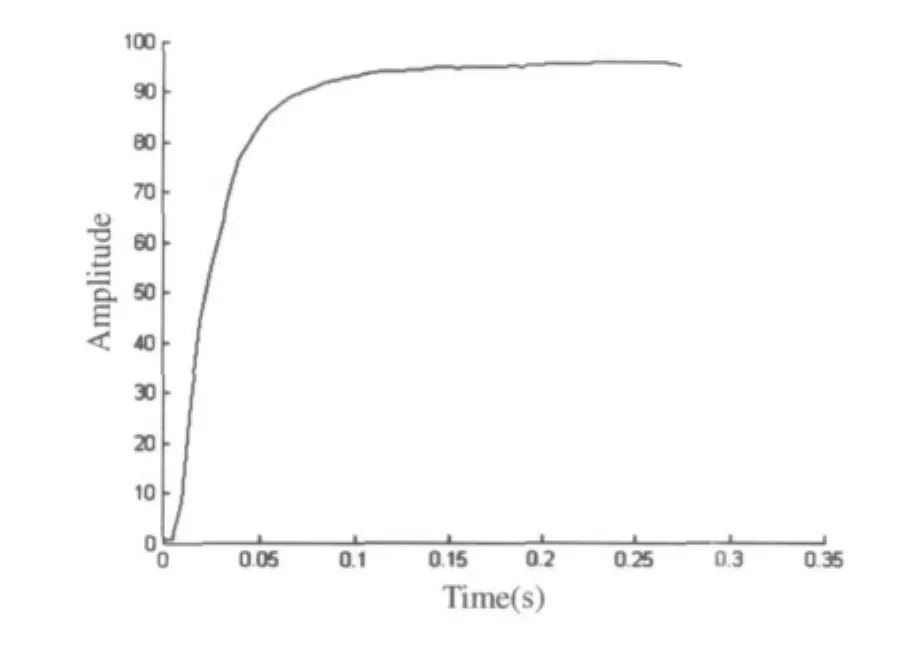
图6 开环阶跃响应曲线图

采用Simulink中的Parameter Estimation工具根据阶跃响应曲线数据，对上述5个参数进行辨识后，得到图7的辨识结果。由该图，可以看出辨识后的结果与实测曲线非常接近，拟合度很高。

图7 参数辨识结果图

5 控制器设计

经过参数辨识，得到该伺服系统中电机电势常数、电机转矩常数、摩擦力矩、黏性摩擦系数和传动系统弹性模量的准确数值。基于这些数据，本文利用Matlab中的SISO工具来进行控制器的设计。由于，现代控制理论是建立在线性系统的基础上。因此，在控制器设计之前需要利用Linear Anlysis工具对系统的开环通道进行线性化处理已得出各部分的开环传递函数。

图8 电流环补偿器设计根轨迹和伯德图

5.1 电流环设计

图9 电流环补偿器闭环阶跃响应

由根轨迹(图8)可知，开环传递函数有两个极点s=0，－527.7，不足以满足性能指标快速的要求，因此在左侧实轴上添加一个零点，再调整其位置和增益，所得闭环阶跃响应(图9，阶跃发生在t=1s)超调为2.6%，调解时间为1ms，幅值裕量为无穷大，相角裕量为87.9°，对应补偿器参数为a=－1000，Kp=126，即 C(s)=

5.2 速度环设计

加入电流环之后，使用simulink—linear analysis模块对速度环开环进行线性化，所得传递函数的zpk形式为:

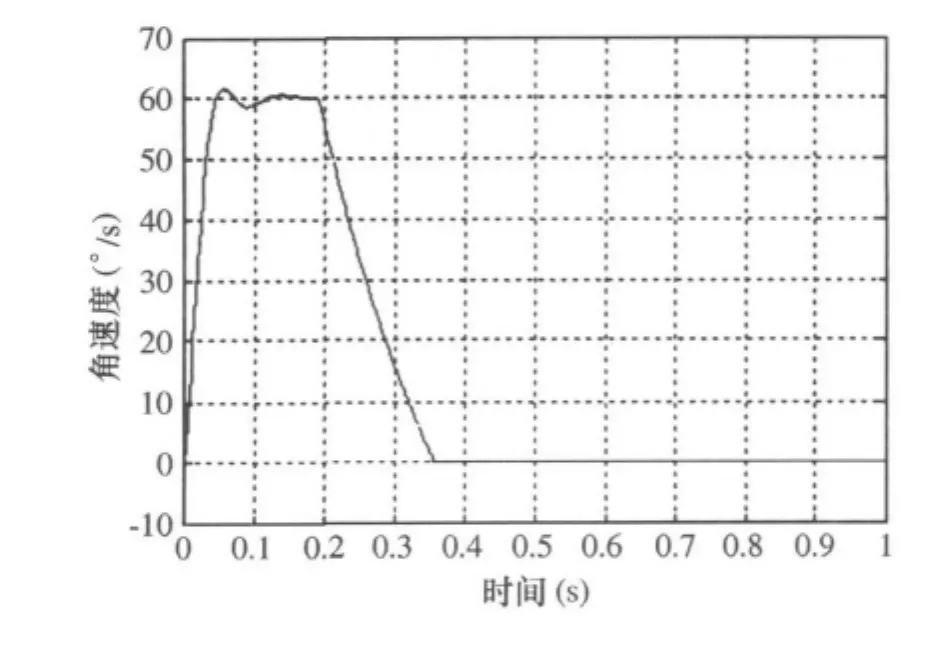
图10 速度环响应曲线(0.2s后为机构碰壁后的速度变化)

另外，电机转动角速度使用陀螺测量，其传递函数H(s)应在sisotool控制器设计结构中体现，

为了保证速度跟踪精度，加入积分环节，开环主导极点为(s=0，－1.837)，下一对极点为(－56.28±j83.26)，故设置零点吸引这两个主导极点向实轴左侧移动，调整增益使其中之一接近零点闭环响应可认为近似相消，另一个实极点幅值足够大从而提升闭环响应的速度。

5.3 位置环设计

加入电流环和速度环之后，使用simulink—linear analysis模块对位置环开环进行线性化，所得传递函数的为:

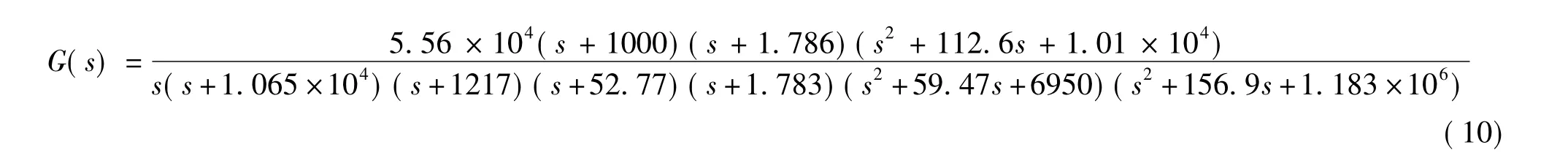
开环系统为I型系统，为了能够精确跟踪位置斜坡指令输入，加入积分器，闭环主导极点为s=0，－1.783，设计思路与速度环类似。

6 代码自动生成

在效果验证前需要完成代码生成，也就是将设计好的控制器变成可以在嵌入式平台上可执行的C语言程序。

6.1 环境构建

进行代码生成并不能在原有的仿真平台上，需要重新搭建专门用于代码生成的平台。该平台以控制算法为主体，配合输入输出接口和数据转换单位来实现，如图11所示。本文通过配置2000系列下的ert工具来完成针对TI公司TMS320LF2812芯片的代码自动生成。

6.2 代码报表生成

通过ert工具完成代码生成后可以自动完成代码报表如图12所示。该代码报表具有模型到代码、代码到模型的双向链接。

可点击模型中的某个模块来方便的查看该模块对应的代码，进而察看该段代码是否按照要求自动生成。

图11 代码生成平台

图12 自动生成的代码报表图

7 效果验证

效果验证是整个设计流程的最后一步，也是最关键的一步。在验证过程中，可将生成的控制算法代码添加到应用程序中对测试平台进行相应的控制。通过观测被测平台的响应效果、分析试验数据，可以验证并调整模型和控制算法，从而形成设计闭环。

图13 角度实测数据图

在本文的测试过程中，发现干摩擦力矩远小于原计算出的0.135N*m。因此，缩小干摩擦力矩的参数辨识范围后重新辨识，最终得出干摩擦力矩为0.01N*m。在新参数下重新调节控制器，得到了较为满意的控制效果，如图13所示。从图13中可以看出系统的响应速度很快，超调较小，定位精度可以控制在0.1°以内，基本满足设计要求。

8 影响伺服系统精度的分析

8.1 干摩擦力矩的影响

干摩擦力矩的大小对跟踪系统会产生不同的影响。例如，当施加 5°的阶跃信号时，按干摩擦0.1898或0得到的响应如图14所示。当阶跃值更小时，在同一组控制器参数下，会比较显著地延长响应的时间。

图14 位置环阶跃响应曲线

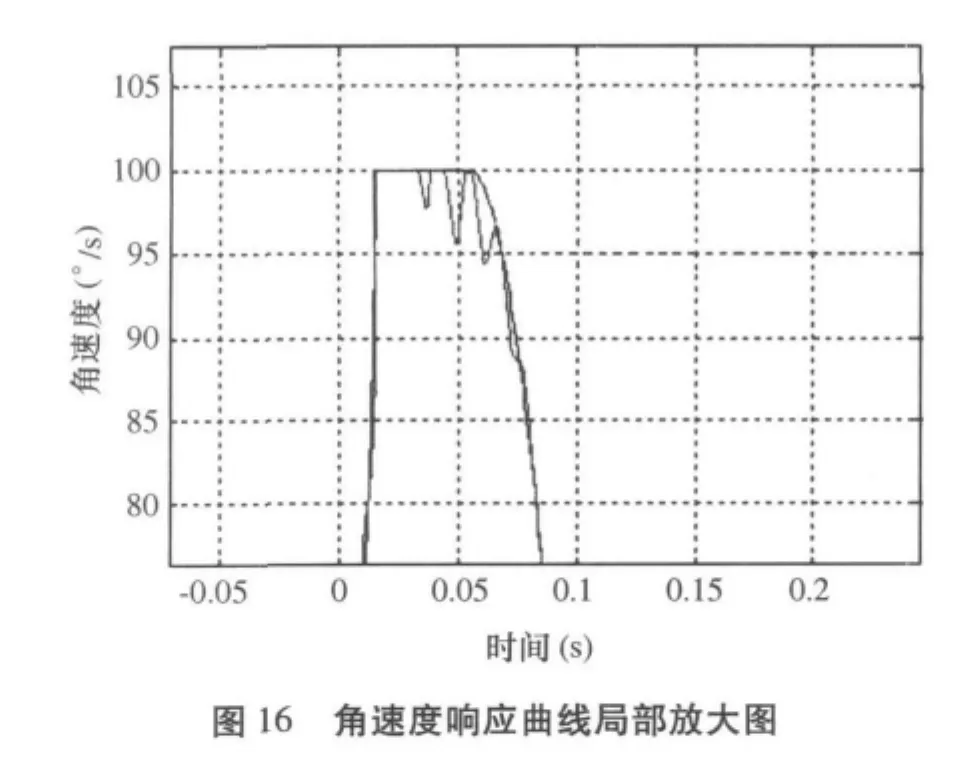
8.2 传动系统机械弹性的影响

图15说明了在弹性模量按参数估计出的182.781或取一个刚性不足50时在10°的阶跃输入下角速度响应图，可以看出传动系统刚性不足时，角速度响应偏慢;而刚性过强，则响应会有颤动。

8.3 传动间隙的影响

从图17可以看出，输入1°阶跃时，在2mrad传动间隙影响下的角度响应有0.0182s的延迟。

综上所述，系统中有各种影响因素，包括干摩擦力矩、传动系统的机械弹性和传动间隙，它们都会对控制系统的设计造成影响。可以采取两种措施来解决问题:a.从系统设计上将以上影响降到最小，如传动系统的刚性要足够、尽可能从结构设计上减小传动间隙等;b.从控制器设计上补偿，利用控制理论设计好控制器后，还需综合各种非线性环节的影响，不断调试控制器，直至达到满意的控制性能。

图17 角度响应曲线

9 结束语

该方法为设计师提供一个良好的理论转化为工程实践的验证窗口和测试平台。通过该方法可以不断地进行设计工作的闭环调整，不仅可以深入地挖掘控制理论，为伺服系统设计提供优越的控制方法，提高技术水平;而且可以更加清晰地了解控制对象，使设计目标更加明确，对问题的分析更加精准。

［1］廖晓钟.控制系统分析与设计［M］.北京:清华大学出版社，2008.

［2］戴忠达.自动控制理论基础［M］.北京:清华大学出版社，1991.

［3］薛定宇.基于Matlab/Simulink的系统仿真技术与应用［M］.北京:清华大学出版社，2002.