二次下变频实现宽带数字波束形成

任泽宇 罗丁利

(西安电子工程研究所 西安 710100)

1 引言

近年来人们研究了很多宽带数字波束形成算法[1～4]，传统的频域处理方法和时域处理方法都能有效实现波束形成，但数据量大，实现复杂，成本较高[5]。为降低计算量及处理复杂度，目前普遍采用的方法为，模拟域通过延时线结构补偿延时，利用去斜技术降低信号带宽，使数据量大为降低[1]。但仍存在只能延时整数倍采样单元、价格昂贵实现不灵活、后期处理需要补偿剩余分数延时等缺陷。

本文采用二次下变频技术:首先在模拟域进行混频，完成去斜工作，降低信号带宽;为消除时延造成的影响，各阵元进行独立的数字下变频;最后经相位补偿完成接收。本方法在有效降低数据量、实现延时精确补偿的同时，可有效降低成本且波束指向更改方便。

2 系统组成及理论分析

本文采用N元均匀线阵模型，在已知信号回波方向的跟踪模式下工作，发射线性调频信号，带宽500MHz，一维距离像分辨力为 0.3m[1]，线性调频信号形式为:

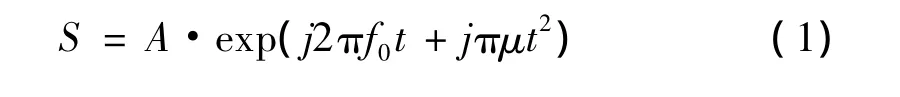
其中A为信号幅度;f0为起始频率;μ为调频斜率。如图1所示，光速c，对于阵元间距d，θin方向回波信号，到达相邻阵元之间的延时为:

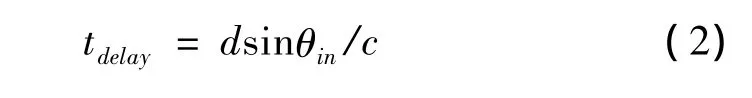
将引起复包络A·exp(jπμt2)的偏移[1]，类似于SAR中的距离徙动现象。

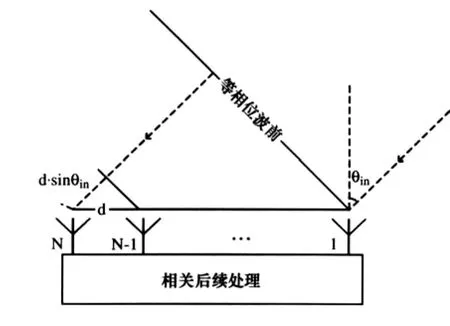
图1 相控阵天线模型

本方法与传统实现方式[1]不同之处为未使用模拟延时线结构。本方法在模拟域进行去斜处理，以降低数据量，为消除延时造成的影响，在数字域各路进行独立的二次下变频，各路数字本振(用DDS实现)频率根据波束指向实时调整而非固定值。本文实现框图如图3所示。

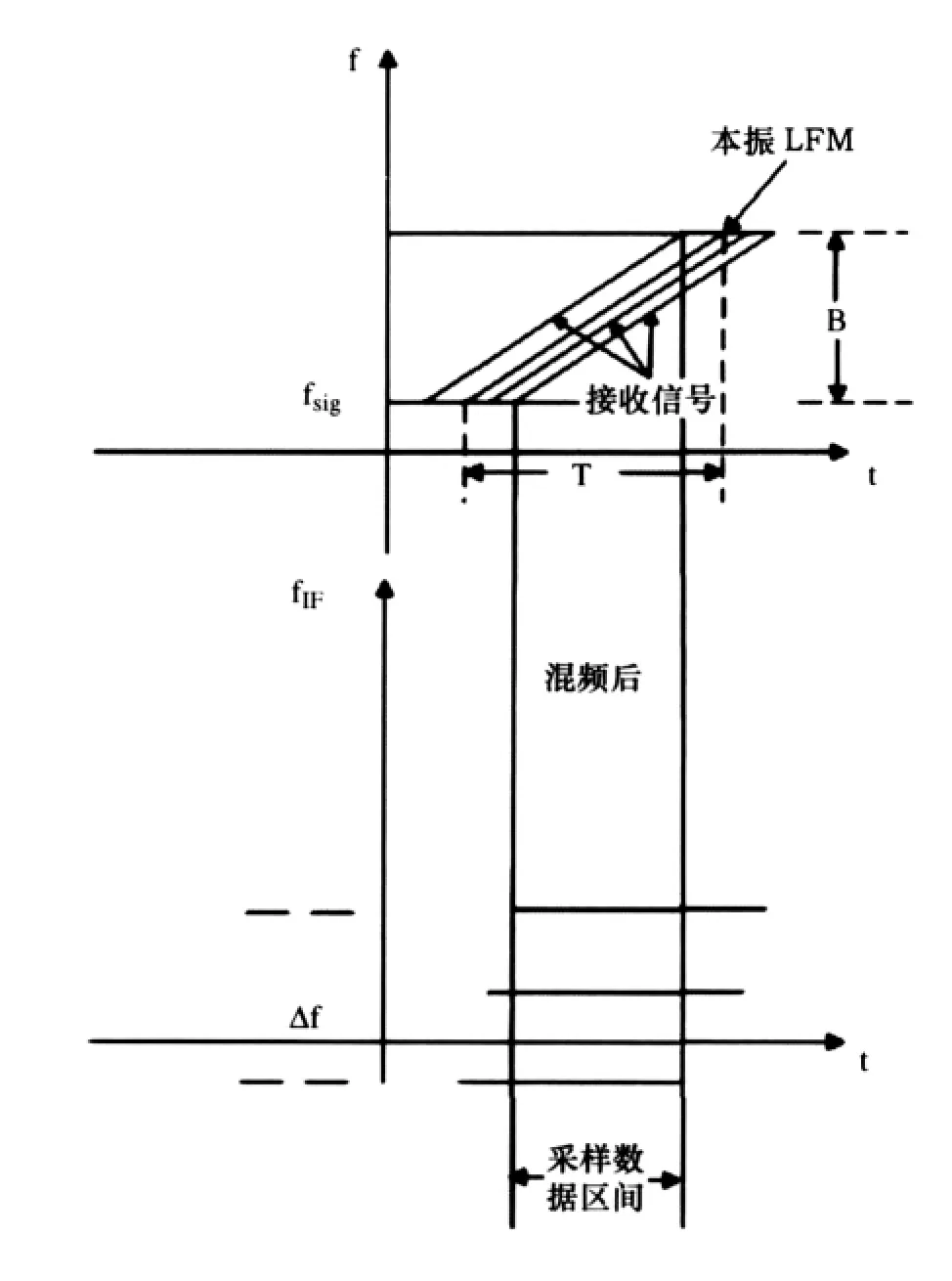
图2 模拟去斜原理[1]

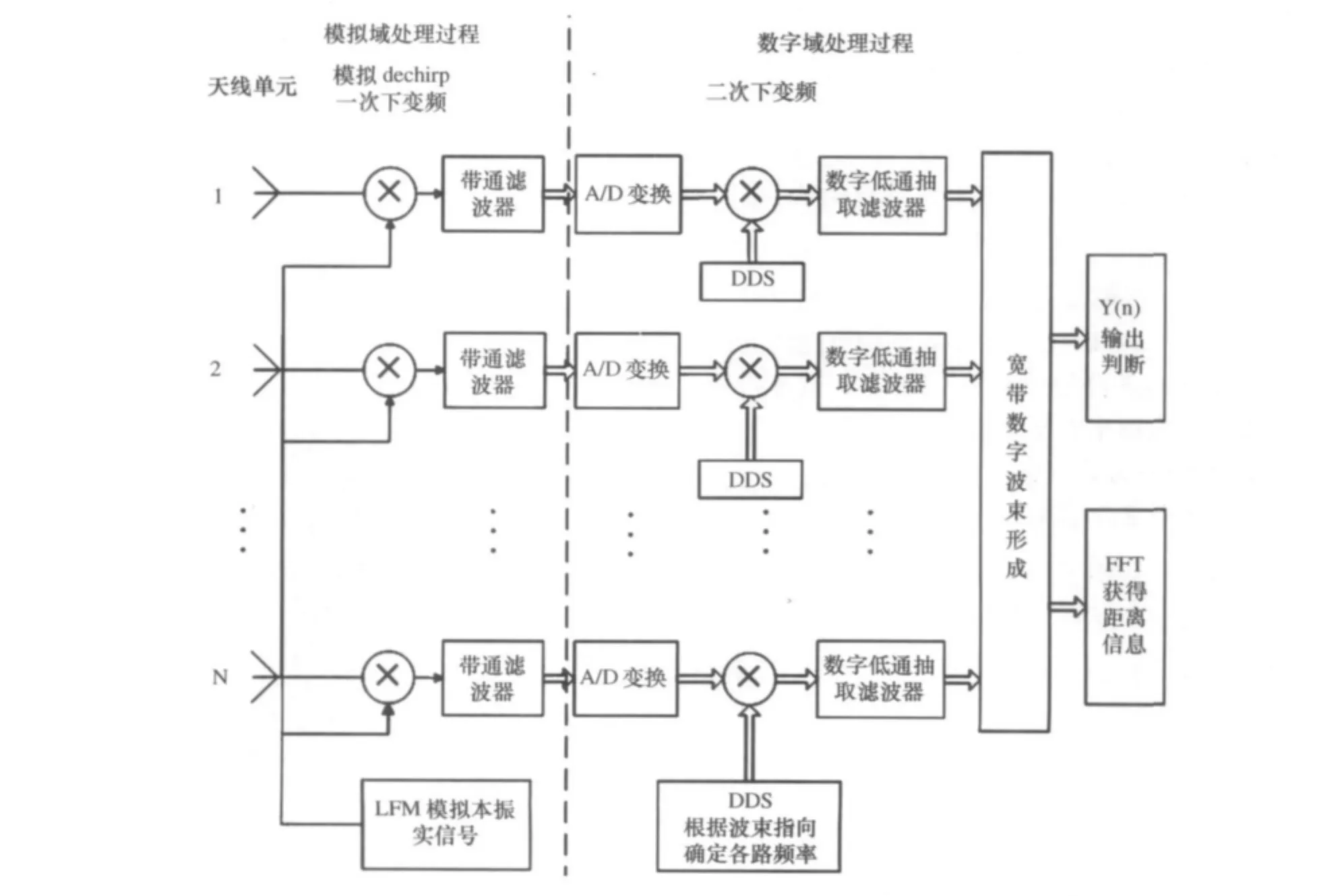
图3 系统实现框图

本文处理过程分析如下。

暂按接收复信号讨论，此时混频不会产生倍频分量，而实际处理中倍频分量会被滤波器滤除。根据(1)、(2)式，第m号阵元接收回波信号Srec形式为:

dt为散射点相对波门起始距离延时;(m－1)tdelay为第m号阵元相对于参考阵元延时。

模拟dechirp信号Sdec为:

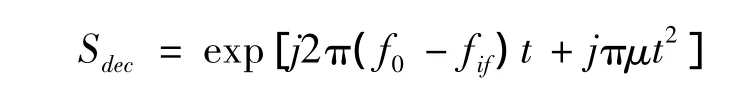
fif为中频频率。

模拟混频后中频信号Sa为:

本文实验条件下(3)式中 μ[2(m－1)tdelay·dt+((m －1)tdelay)2+dt2]很小(＜0.01)，影响很小可将其忽略。则

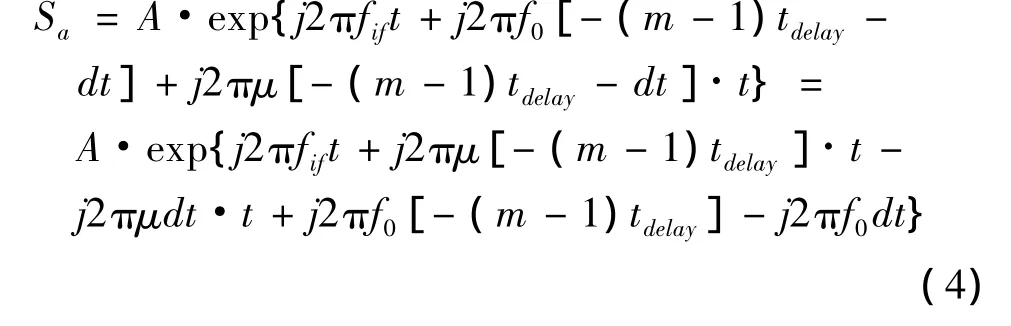
由(4)式可得模拟去斜后第m个阵元信号频率为:fif+ μ[－ (m － 1)tdelay]－ μdt，回波到达阵元间延时tdelay将导致各路信号频率不同。本文利用数字二次下变频消除频率差异从而消除延时影响。第m个阵元DDS频率为fif+μ·[－(m －1)tdelay]。

数字二次下变频后第m个阵元信号为:式中t'为经抽取后离散采样时刻。

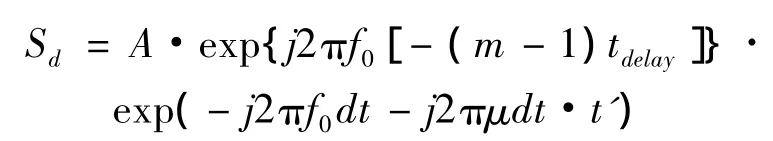
第m个阵元相位补偿权值为:w=exp[－j2πf0(m－1)tdelay]，经加权后波束形成结果为:

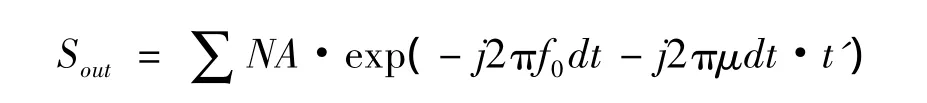
上式即为最终输出信号形式。不同散射点信息，对应上式中dt不同，波束形成后表现为信号频率不同，傅氏变换后便可获得散射点信息。

3 相关问题讨论

指向更改:当接收波束指向需要发生变化时，模拟混频信号Sdec不必更改，数字下变频更改DDS相应参数即可，权值更改tdelay即可。

调频斜率:模拟去斜后各路信号频率与调频斜率、入射角度、阵元间距等有关，为满足中频无损失接收，各路信号都应落入接收机带宽内，需满足|μ·dt|＜Bj及|(M －1)μdsin(θin)/c|＜ Bj，Bj为中频接收机带宽，根据系统约束设计μ。

结果正确性判定:完全理想情况下，各路接收信号经过二次下变频及相位补偿后，信号时域波形应完全重合，存在噪声时，起伏不会很大，利用某几路输出信号功率方差作为第一判决条件;输出波形为若干点频信号叠加，应呈现周期性变化，此为第二判决条件。

4 性能分析及仿真验证

仿真模型:均匀线阵64个阵元，阵元间距为4.62cm，回波形式为LFM实信号，带宽500MHz，雷达工作频率3GHz～3.5GHz，信号持续时间100μs，采样波门长度96μs，信噪比30dB，噪声为高斯白噪声，波束指向10°，中频频率60MHz，射频采样频率12GHz。

中频25抽取，中频采样率为480MHz，基带24抽取，基带采样率为20MHz。

理想情况(无噪声)下接收复包络如图4所示。

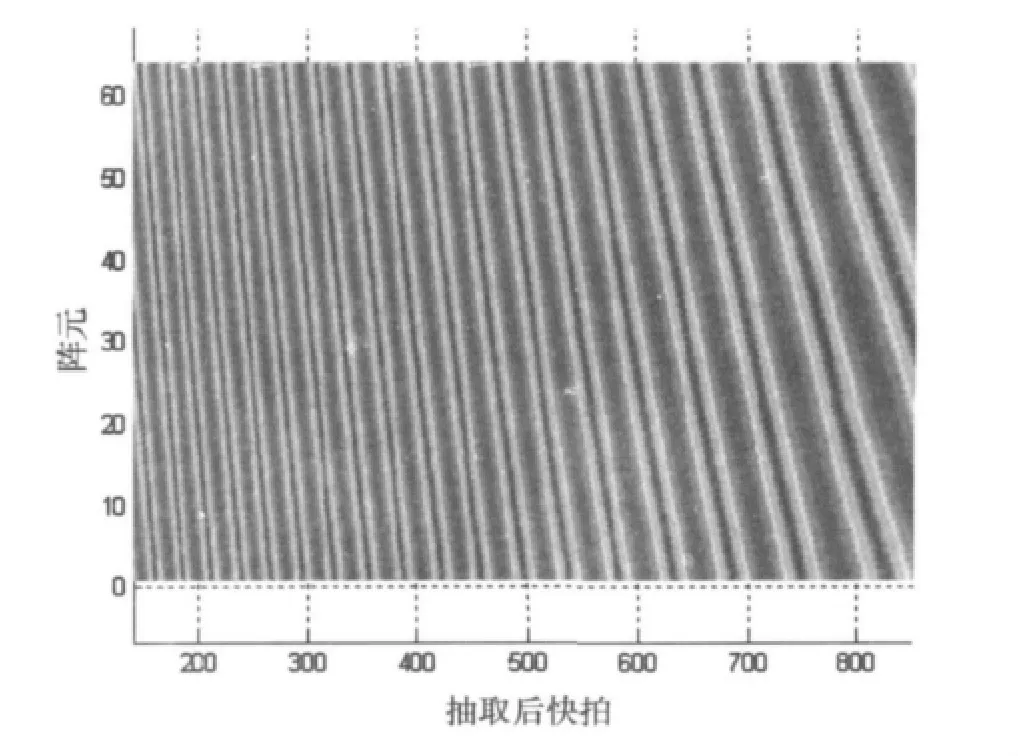
图4 接收信号复包络

图4与理论分析一致，非法线方向回波到达各阵元的延时引起复包络偏移。

仿真实验一:先进行线阵静止点目标即一个散射点情况讨论，散射点相对30km波门起始距离0m，我们关心±150m范围信息。

图5为经过本文方法处理，相位补偿后基带时域波形，根据此时假定的点目标位置，处理后基带各阵元信号都为直流信号。

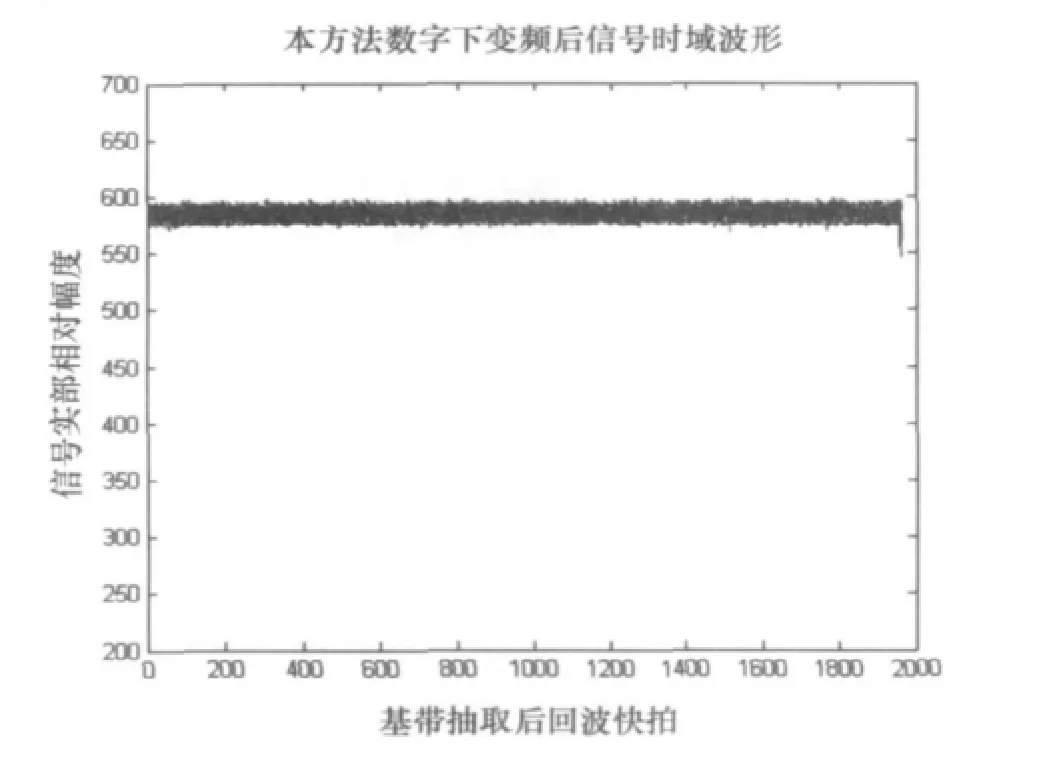
图5 采用本文方法基带输出信号时域波形

当二次下变频各路数字本振频率相同(DDS频率取为fif)时，相位补偿后时域输出波形如图6所示，与理论分析一致，各路信号频率不同。

图6 未采用本文方法基带输出信号时域波形

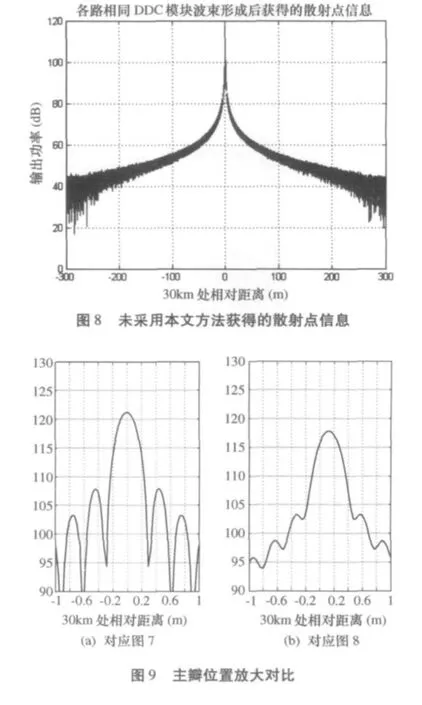
图7为图5中信号波束形成及傅氏变换后获得的散射点距离信息，距离估计为0.0000m。波束形成及FFT过程信号功率积累，信号的输出功率相应增加。

图7 采用本文方法获得的散射点信息

图6中各路信号频率较低且相差较小，波束形成及傅氏变换后将造成距离估计误差、主瓣展宽、频谱副瓣畸变等影响如图8所示，此时距离估计为0.1099m。图9为图7及图8的主瓣位置放大对比。

仿真实验二:进行线阵分布式目标即三个散射点情况讨论，信号相对波门起始距离－0.3m、0m、15m，其他条件同实验一，处理过程与一个散射点情况相同。

本方法将目标距离信息转化为频率信息，此时波束形成结果为三个不同频率点频信号叠加，输出信号时域波形如图10所示，各路信号基本重合且呈现周期性变化。

图11为图10中信号波束形成及傅氏变换后获得的散射点距离信息，距离估计为:－0.3662m、0.0732m、15.0000m。本方法可实现宽带波束形成并有效分辨多个散射点。与脉冲压缩处理相似，两个散射点间距离达到分辨力极限时，将导致距离估计误差[6]。

5 结论

本文提出了一种有效实现宽带信号接收的数字波束形成方法。通过数字域各路独立的下变频处理，可有效消除延时引起的影响，与传统方法相比可有效降低数据率、降低系统复杂度、降低成本，波束指向更改方便，易于工程实现。理论分析和仿真实验结果都论证了本方法的有效性。

[1]王德纯.宽带相控阵雷达[M].北京:国防工业出版社，2010.

[2]朱维杰，孙进才，曾向阳.宽带波束形成器的自适应综合[J].声学学报，2003，(3).

[3]Yang Yixin，Wan Chunru，Sun Chao.Adaptive design of FIR filter with applications in broadband beamforming[J].2004 IEEE Region 10 Conference.

[4]唐建生.时域宽带波束形成方法及实验研究[D].西安:西北工业大学硕士论文，2004.

[5]张灵珠，杨晓冬，刘枫.时域和频域宽带数字波束形成方法研究[J].系统仿真技术，2008，10.

[6]Bassem R.Mahafza著，罗群等译.雷达系统分析与设计(MATLAB版)[M].北京:电子工业出版社，2008.