基于模式空间的宽带DOA估计算法研究
刘春静
(中国电子科技集团公司第三十八研究所 合肥 230088)
1 引言
DOA估计是阵列信号处理领域的一个重要研究方向,而宽带信源的DOA估计又是其中的一个难点问题。与窄带测向不同的是,宽带情况下阵列输出的相位差不仅依赖于波达角的方位,而且与信号频率有关,因此窄带的估计方法就不适用了。
传统的宽带DOA估计方法如相干子空间(CSS,coherent signal subspace)[1,2]、双边相关变换(TCT,two - sided correlation transformation)[3]等都是通过构造聚焦矩阵的方法将不同频率上的信号空间聚焦到参考频率上,然后对聚焦后得到的单一频率协方差矩阵进行窄带处理。在该类算法中出于构造聚焦矩阵的需要,必须对信号波达角进行预估计,研究表明,预估角度的个数和取值大小对算法性能影响很大[4]。为了避免预估计结果对后续处理的影响,文献[5]根据阵列导向矢量的Jacobi-Anger展开式提出了基于模式空间分解的宽带DOA估计算法,其基本思想是将导向矢量中的频率信息和波达角信息分开后,再利用Bessel函数的衰减特性将其截断后构造协方差矩阵进行处理。本文将该算法扩展到任意几何结构的天线阵列,并详细分析了最优聚焦矩阵和参考频率的选择方法,最后验证了算法的有效性。
2 信号模型
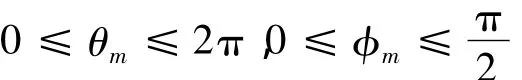

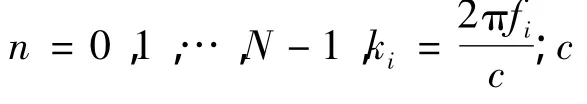


()H表示矩阵的复共轭转置,E[·]表示求期望运算。
3 模式空间处理算法
3.1 模式分解原理
在传统的宽带DOA算法中,为了减小聚焦变换误差,需要对信号到达角进行预估计,研究表明预估角度的准确性直接决定了最终估计方向的精度[4]。为避免预估算法性能的影响,我们可以通过模式空间分解的方法将阵列导向矢量中的频率变量和角度变量分离后再聚焦,根据Jacobi-Anger展开[6],得


考察球形Bessel函数Jl(x)的性质可知,对于给定的x,随着u的增大,Jl(x)逐渐趋近于0。因此对于孔径有限的天线阵列,且入射信号带宽有限时,导向矢量可用(5)式的有限项来表示,只要选择足够大的多项式阶数,就能保证足够小的误差。
3.2 聚焦矩阵的选择
将(5)式截断后保留前L项得


设Ti为第i个频点处的聚焦矩阵,文献[5]中提出了两种选择聚焦矩阵的方式:
a.不需要参考频率
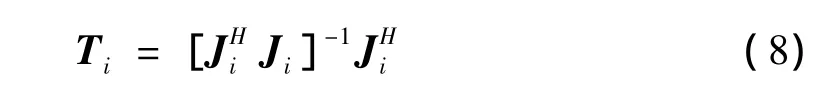
b.需要参考频率
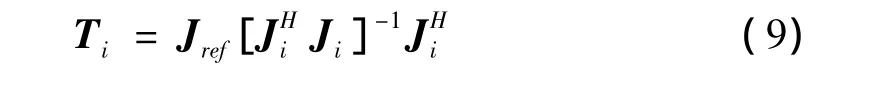
其中Jref为所选参考频率的Bessel函数截断矩阵。
采用(8)、(9)两式聚焦的缺点主要有以下两个方面:a.为了使JHiJi可逆,必须选择合适的天线阵元坐标位置,比如对于直线阵列来说,应该将阵列中心位置作为参考原点;b.聚焦矩阵的非酉特性使聚焦后的信噪比降低,即存在聚焦损失,这一点将在后面的仿真中予以证明。
为了克服以上两个缺点,使聚焦后的阵列流型与所选参考频点阵列流型间的误差最小,可以通过求解下式求得最优聚焦矩阵:

其中Aref为所选参考频率的导向矢量矩阵,‖·‖F为矩阵 Frobenius范数,I为单位矩阵。根据(6)式,(10)式可等价为:
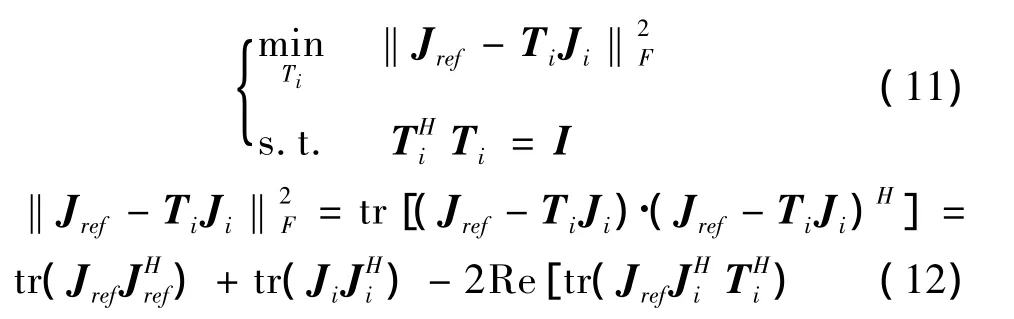
其中tr(·)表示求矩阵迹,Re(·)表示求实部运算。当截断长度L和参考频率一定时,(11)式等效为在Ti为酉矩阵的约束条件下使 Re[tr(Jref)]最大。

其中U和V分别为矩阵C的左右奇异向量矩阵;对角阵Σ =diag(σ11,…,σNN);σnn为C的第n个奇异值。因此,


当|Znn|=1时(15)式取等号,此时Ti的一个解为:

在白噪声情况下,宽带信号的协方差矩阵为:

其中K为划分的频点数,σ2i为噪声功率,聚焦变换后的协方差矩阵为:

定义聚焦损失因子为[7]:

将(16)式代入(19)式,根据矩阵迹的性质很容易求得g=1,即当Ti为酉阵时无聚焦损失。
3.3 最优参考频率
根据(11)式,以各频点处的拟合误差之和最小为准则,最优化表达式如下:

将(12)式代入(20)式中,得:

其中σn(·)表示矩阵的奇异值,当截断长度L和频

通过一维搜索即可求解出最优参考频率。
综上所述,只要根据(22)式和(16)式求出参考频率和聚焦矩阵,然后由(18)式计算RzT,最后采用MUSIC等窄带算法估计出信源方位。
4 仿真实验
实验1 仿真条件为18元均匀直线阵,三个等功率宽带信号分别从38°、42°和60°方向入射到该阵列上,信噪比为10dB,其中第二个信号为第一个信号的多径分量,时延为0.125s,第三个信号与前两个信号互不相关。信号中心频率均为100Hz,带宽为40Hz,处理频点数为33,采样点数为2112个快拍,Bessel函数的截断长度取14。图1~图3中的每个仿真点均是通过200次独立实验后取平均得到的。
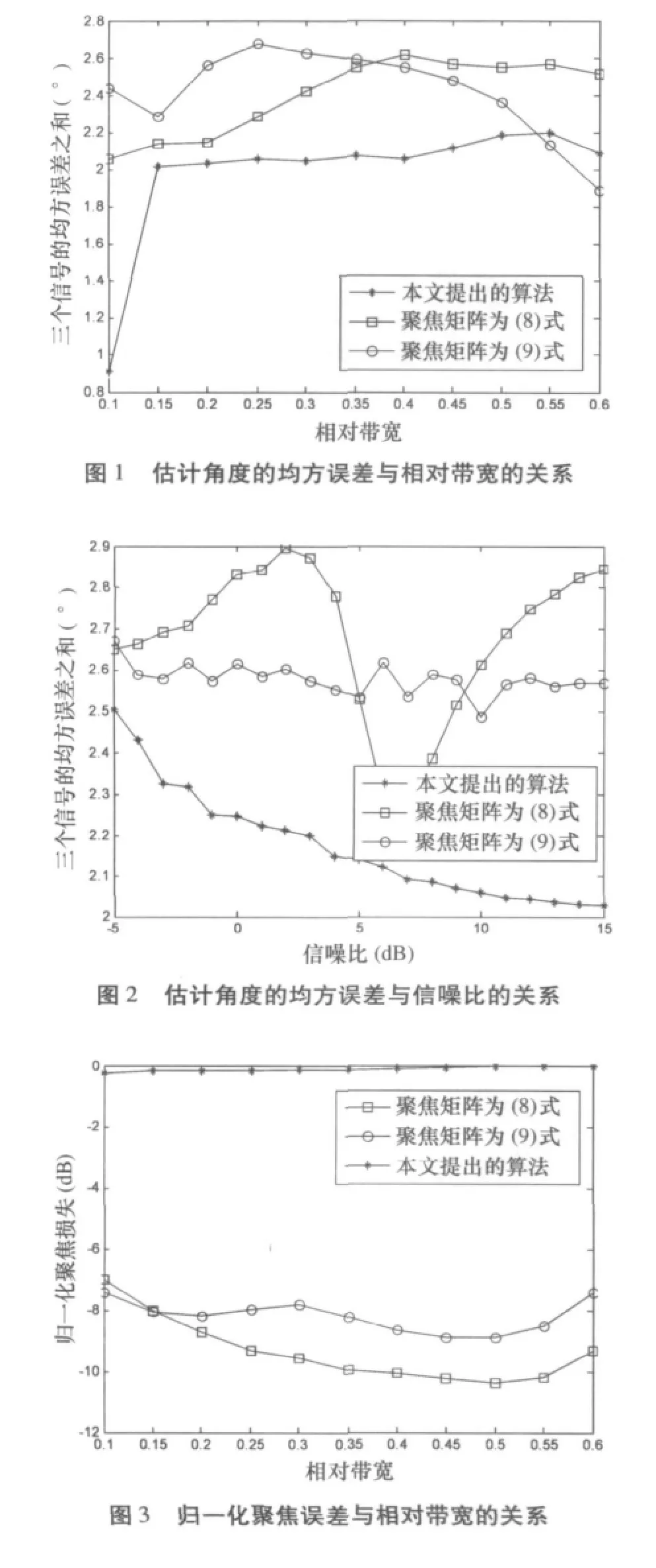
图1和图2分别为估计角度的均方误差之和与相对带宽和信噪比的关系(我们将本文提出的算法,即(16)式,称为算法一,将(8)、(9)式分别称为算法二和算法三)。随着入射信号带宽的增大,采用算法一得到的均方误差曲线波动很小,且误差值低于后两种算法,只是在部分高带宽区域略高于算法三;在图2中可以看到,算法一的均方误差曲线表现出很好的收敛特性,算法三的曲线则表现出明显的不稳定性。另外从图3中聚焦误差与相对带宽的关系曲线也可以看出,算法一最好,算法三次之,算法二的效果最差。
图4是典型的归一化拟合误差与频率的关系曲线图,通过搜索该曲线上的最小值就可以求出最优参考频率,从而验证了式(22)的正确性。

实验2下面验证模式空间算法在二维平面阵中波达角估计的有效性。假设阵列为8×6标准矩形阵[8],三个等功率宽带信号的入射俯仰角均为45°,方位角为40°、70°和 110°,且第三个信号为第二个信号的多径分量,时延为0.125s,第一个信号与其余两个信号互不相关。处理频点数为66,采样点数为4224个快拍,Bessel函数的截断长度取20,其余条件与实验一中相同。从图5的仿真结果中可以很清晰地看到三个明显的谱峰,正确分辨出了三个不同来向的入射信号。
5 结论
本文通过详细分析模式空间宽带DOA算法中最优聚焦矩阵和参考频率的选取方法,指出了提高算法性能的有效途径。但是值得注意的是,Bessel函数中截断阶数的选择也是制约算法性能的关键因素,因此有必要进一步讨论不同阵列结构、不同信号环境下截断阶数的取值问题,这也是算法实用化的重要步骤。
[1]Wang H.and Kaveh M.Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wide-band sources[J].IEEE Trans.on ASSP,1985,33(4):823-831.
[2]Mahata K.A subspace algorithm for wideband source localization without narrowband filtering[J].IEEE Trans.on SP,2011,59(7):3470-3475.
[3]Valaee S.and Kabal P.Wideband array processing using a two-sided correlation transformation [J].IEEE Trans.on SP,1995,43(1):160-172.
[4]Swingler D.and KROLIK J.Source location bias in the coherently focused high-resolution broadband beamformer[J].IEEE Trans.on ASSP,1989,37(1):143 -145.
[5]Abhayapala T.D.and Bhatta H.Coherent broadband source localization by modal space processing[C].IEEE 10thInternational Conference on Telecommunications,2003,1617-1623.
[6]Abhayapala T.D.Modal analysis and synthesis of broadband nearfield beamforming arrays[Z].Ph.D.dissertation,Research School of Information Sciences and Engineering,Australian National University,Canberra ACT,1999.
[7]Doron M.A.and Weiss A.J.On focusing matrices for wideband array processing[J].IEEE Tans.on SP,1992,40(6):1295 -1302.
[8]Trees H.L.V.Optimal array processing,Part IV of detection,estimation,and modulation theory [M]. Wiley - Interscience, New York,2002.

