有效追问 活力课堂——《异面直线》教学案例与点评

葛建华

（南通市如东高级中学，江苏 南通 226400）

课堂教学的本质是“对话”与“合作”，课堂提问作为师生课堂对话的主要形式，不仅可以检测学生的知识掌握情况，更重要的是能够引发学生对问题的思考，从而达到促进学生问题意识的形成和实践能力的发展，有利于后续教学活动的展开。有效追问，作为课堂提问的一种重要形式，能激活学生思维，引发学生深度思考，推动学生思维创新，有效追问就像一条不断延伸的纽带，使教学活动串成一个和谐整体，将课堂变成一个富有活力的对话阵地，能有效地吸引学生，引起学生的求知欲，激发学生去积极思维，主动探求知识。那么，在课堂教学中，如何实现有效追问呢？下面笔者拟结合苏教版数学必修二p25《异面直线》的公开课教学经历，谈谈自己的做法与体会，和同行共同探讨。

一、知识回顾后追问，引入教学话题

上课伊始，给出问题：前面我们学习了空间两直线的位置关系，请大家回顾一下，空间两直线有怎样的位置关系？

生：平行、相交、异面。

师：其中，异面直线是如何定义的？

生：我们把不同在任何一个平面内的两直线叫异面直线。

师：很好！（追问）异面直线对我们来说，是个“新生事物”。对这个“新生事物”，你有怎样的想法？或者说，你准备如何对它开展研究？

生：我想从如何判断两直线是否为异面直线开始研究。

[特级教师点评]通过追问引出课题，不仅仅是要让学生学习知识，更重要的是教给学生学习和研究问题的意识和方法。

二、通过追问，引导学生实现数学方法建构

问题情境：如何判定（证明）空间两直线是否为异面直线？

追问：通过前面的学习，你有哪些方法？

引导学生发现依据：①空间直线的位置关系分类：不平行、不相交（排除法）。②异面直线的定义。结合具体的例子让学生思考如何操作：

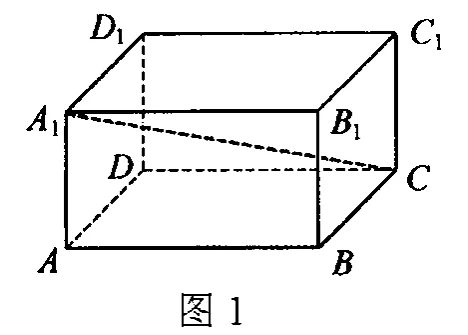
问题：在长方体中ABCD-A1B1C1D1，哪些棱所在直线与直线A1C是异面直线？

生：显然所有的棱都与直线A1C不平行，因此只需剔除与直线A1C相交的棱，即剔除过点A1和C的6条，剩下的都是。

师（追问）：以棱为例，我们已经得到直线与异面，如何证明？

学生发现可以用排除法，即排除平行和相交的情形。此时，进一步追问：还有没有其他方法？

学生发现还可以用异面直线定义来证明。

此时追问：异面直线的定义是“不同在任何一个平面内的两直线”，如何证明直线AB与A1C不同在任何一个平面内？

引导学生提炼出反证法的基本步骤：反设→归谬→得出正确结论，并利用反证法证明该问题。

得出异面直线判定定理之后，再请学生依据判定定理在图1中寻找与BD1异面的直线。

学生得出答案后，再次追问：解题的关键是什么？学生发现寻找合适的基础平面α是关键。

[特级教师点评]通过追问，引导学生发现并提炼解决问题的方法，能洞察问题的本质，让学生的思维活动有深度、有广度，有效活化学生思维，课堂因此变得更具活力。

三、通过追问，让学生体验数学知识的形成过程

师：给出两直线是异面直线，对它们之间的关系能否进一步刻画？

要求学生用两只笔摆成异面直线形状，并通过位置变化（仍保持为异面直线）探求其内部关系。

通过模型显示，学生发现两条异面直线也可形成大小不同的“角”，两条异面直线也可以形成不同的“距离”，此时追问：如何寻找一个合适的几何量来刻划两条异面直线之间的倾斜程度和远近程度呢?让我们先考虑异面直线的“角”。

学生意识到转化为平面角（降维方法，化归思想），从而生成异面直线所成角的定义：如图3，为异面直线，经过空间任一点，作a′∥a，b′∥b，我们把直线a′和b′所成角（锐角或直角）叫做异面直线a，b所成角。

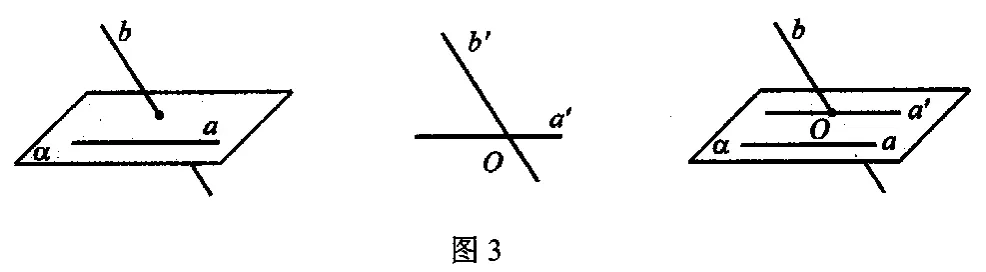
追问：异面直线所成角定义中点O是任意选取的，能保证角的大小唯一吗？

学生发现利用等角定理即可说明。

二次追问：根据定义，异面直线所成角应在怎样的范围内？[0°，90°]。

再次追问：一般地，如何求两异面直线所成角？平移直线。

拓展追问：在平面几何中，我们是如何定义两直线垂直的？作为异面直线，你认为它们有可能垂直吗？如果可以，怎样定义合理？

[特级教师点评]“学成于思，思源于疑”。通过追问，引发学生的认知冲突，让学生始终处于愤悱状态，让学生在解决问题的过程中体验知识的形成过程，在潜移默化中掌握数学思想方法。

知能训练，给出问题：已知ABCD-A1B1C1D1是棱长为a的正方体（图4）。

①正方体内哪些棱所在直线与直线BC1是异面直线？

②求异面直线AA1与BC1所成角。

③求异面直线BC1与AC所成角。

学生练习，巡视指导。在学生给出答案后，再追问：你能给出异面直线所成角的求角步骤吗？学生发现需经历作→证→算→结论的过程。其中，异面直线所成角的平面角是如何作出的？引导学生发现点的选择是关键，通常在其中一直线上或利用中点（中位线）来作。

最后，通过设问让学生进行课堂小结：通过本节课的学习，你掌握了哪些知识和数学思想方法？

知识：①异面直线判定（证明）方法；②异面直线所成角；③思想方法：化归思想、排除法、反证法。

拓展延伸（追问）通过本节课的学习，大家对异面直线的判定和异面直线所成角有了清晰的认识。在学习中，我们发现异面直线间的位置刻画除了“角”，还有“距离”，那么，异面直线间的距离又该如何刻画呢？这个问题留给大家作为研究性学习课题。

[特级教师点评]卢梭曾经说过：“问题不在于告诉他一个真理，而在于教他怎样去发现真理。”有效的数学教学应当是教师启发（追问）与学生探究相统一的过程。追问的时机是学生处于“愤与悱”的心理状态，追问的目标是“举一反三”，追问的原则是“道而弗牵，强而弗抑，开而弗达”，从而使学生处于主动地位（学生主动思考到“愤”与“悱”的状态），而不是被动地位（学生被教师的一系列问题所牵制）。教师追问的问题应当体现数学知识的本质特征，要“淡化形式，注重实质”，揭示探索的思考过程，将数学的学术形态转变为教育形态。通观本堂课，教者以思维训练为主线，以知识延展为手段，渗透数学思想方法，通过追问的形式，有效激发学生活力，有效地提升学生的数学学科素养。

[1]何明.心智 在一题多解中激活[J].中学数学教学参考，2007（11）.

[2]王晓东.有效提问：本真数学课堂教学的深层追问[J].教学月刊中学版，2009（6）.

[3]缪林.浅析数学课堂中的一题多变[J].中学数学月刊，2008（7）.

[4]陈唐明.和谐互动 教学相长[J].数学通报，2009（10）.