如何引导学生从“操作工”到“探究者”——以“圆的周长”为例，谈学习方式的改进

李继军

（上海市松江区教师进修学院，上海 200000）

“动手实践”作为新课程倡导的重要学习方式之一，它越来越受到广大数学教师的重视。实践表明，动手操作和实践过程能刺激学生的知觉，丰富学生的感性认识与表象，能促进学生在做中主动探索知识，从而感悟与建构数学知识。但在引导学生通过动手操作进行建构知识和探究规律的过程中，还存在着一些认识和实践上的偏差。其中一个突出的问题是，学生的动手操作活动往往只是按照教师的“指令”行动，缺少应有的数学思考和实践反思。这样的操作活动，正如我国著名特级教师顾汝佐先生所称的——学生只是做了“操作工”，往往是动手不动脑，“活动了身体而休息了大脑”，在很大程度上是一种“假探究”。下面以“圆的周长”教学的三个片断为例，谈谈如何引导学生从单纯的“操作工”成为真正的“探究者”。

一、从“教师直接发出操作具体指令”到“先让学生提出操作活动设想”

【片断描述】

对于如何引导学生进行探究活动，该教师分为两个层次加以引导：一是圆的周长的长短与什么因素有关？教师出示3个直径不同的圆（图略），提问：①你认为哪个圆的周长最长？哪个最短？②你认为圆的周长取决于圆的什么？通过学生的回答老师归结引导为“圆的周长与它的直径有关。直径长，该圆的周长就长；直径短，该圆的周长就短。”二是圆的周长与直径之间究竟有何关系？教师请各小组拿出事先准备好的硬币、铁环、圆瓶盖和圆形厚纸片，选择合适的方法测量出它们的周长和直径，填在相应的“学习单”中（见下表1前3列内容要求），为下一环节引导学生观察、发现规律作好准备。

【问题探讨】

引领学生经历圆的周长计算公式的探究过程，是本课教学的一个重要目标。教师根据教学内容的特点采用探究学习的方式，符合规则学习的内在要求。本教学片断中有两点值得肯定：一是教师通过有层次的引导明确探究的问题指向，即圆的周长与直径直接相关。这一教学法处理体现了数学的研究意识。二是“学习单”的使用，为学生通过动手测量活动所直接获取的数据，提供了比较恰当的载体，便于学生下一步的观察与发现。但该教学中存在着一个较大的缺陷：即探究圆的周长与直径之间究竟有何关系，是教师直接发出了操作的具体“指令”，学生只是根据相关“指令”进行圆形物体的周长与直径的测量。这种操作活动没有学生的探究需要和预先的实践思考，学生仅仅是按照教师的指令“操作”而已。显然，这样的操作活动往往只是停留在形式上，学生更多表现的是“操作工”角色，而不是动手实践活动中的积极“思考者”和“探究者”。

【教学重建】

改进的关键就是促进动手操作活动成为学生探究“圆的周长与直径之间的关系”所需，来自于观察与发现所依赖的研究数据所需。当老师提出“圆的周长与直径之间究竟有何关系”这一探究性问题以后，教师要给予学生一定的思考时间，重在引导学生自己提出研究的设想：要研究两者之间的关系，我们可以选择几个直径不等的圆，测量出它们的周长和直径，看看它们之间到底有何规律。只有真正引发了学生进行数学思考的实践活动，退一步讲，即使学生没有提出操作活动的设想，那也是有教学价值的，至少学生经历了适度的挫折，引发了必要的反思。在此基础上，教师再进行一定的引导：为了便于测量，大家可以使用圆形的物体，把测量的结果填在相应的“学习单”中。可见，从“教师直接发出操作具体指令”到“先让学生提出操作活动设想”，凸显了操作活动的目的，促进了学生学习角色的转变，成为探究活动的主动参与者。

二、从“教师直接告知观察的视点”到“提升观察与发现规律的空间”

【片断描述】

当学生按照教师的要求完成测量后，教师向学生提醒道：“别忘了把周长除以直径得到的商填在表格中，得数可以保留两位小数。观察这些数据，你有何发现？”当然，一部分学生已根据“学习单”上的提示完成填表，剩下的同学在教师的提醒下完成。经过反馈交流，教师选择了四个具体物品数据填写在下面表格（如表1），并引导学生观察发现：“你们发现周长与直径有何关系？”通过小组交流，大家的意见趋于一致：圆的周长总是直径的3倍多一点。在此共识下，教师引出圆周率这一概念以及简要介绍我国古代数学家祖冲之的贡献，顺利推导出圆周长的计算公式：圆周长=圆周率×直径，并用字母表示为c=仔d或c=2仔r。

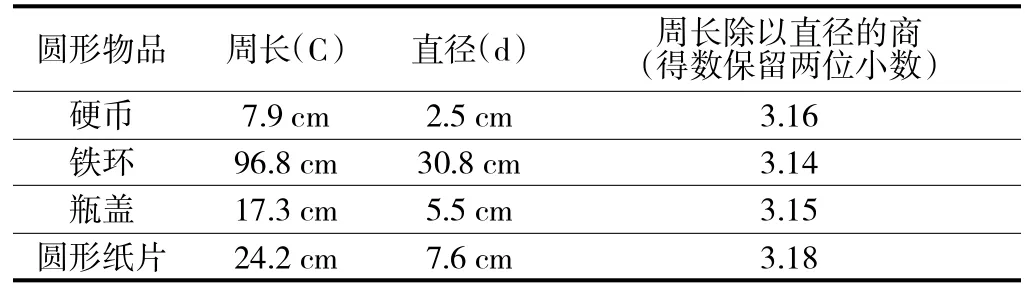
表1

【问题探讨】

面对学生测量获得的数据，教师在“学习单”中所给予的直接提示，随后当学生在完成测量后又进行及时提醒。其目的就是把观察的视点及时告知学生，使学生能顺利地发现圆的周长与直径之间的内在关系：“圆的周长总是直径的3倍多一点”，从而推导出圆周长的计算公式。但是，在发现规律和推导公式的过程中，很大程度上学生成了形式上的发现者和探究者,还是缺少主动思考和真正发现的探究历程和体验。严格来说，其学习方式还是被动的接受式学习。

【教学重建】

根据以上的分析，本教学环节可以作这样的改进：应去掉“学习单”中给予的直接提示和随后进行的及时提醒，如学习单中以“两者之间有何关系？”为提示语。这样，既旨在提升学生思考和探究的空间，又暗示发现规律所涉及的关键因素，明确思考与发现的范围。教学中，如果学生还是不能发现规律，这时教师再给予提醒：“把周长除以直径。观察得到的商，你有何发现？”有了这样的思考与相应的动手操作活动，即使学生没有成功，那也是具有宝贵的教学价值的，至少学生经历了观察、操作、猜想和验证等一系列数学认识活动。据此“学习单”可以作这样的改进（如表2）

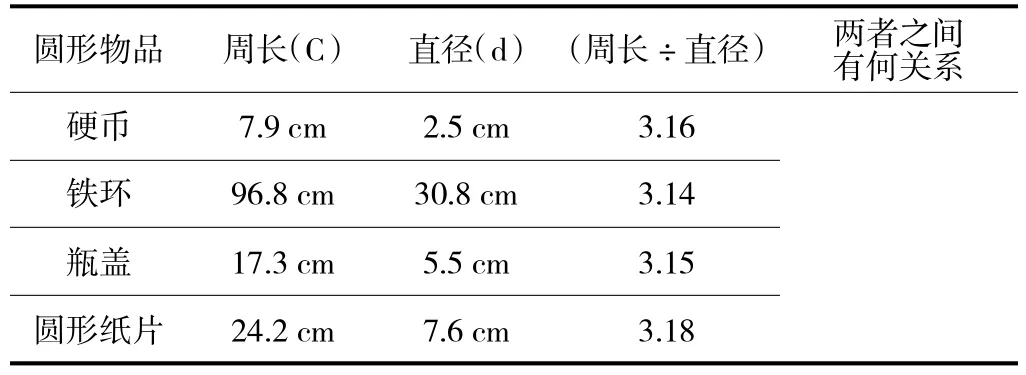
表2

三、从“让学生单纯的实践应用”到“引领学生经历高认知的思维活动”

【片断描述】

巩固知识阶段，教师设计了实践活动作业：拿出一张边长是5 cm的正方形纸，请学生在图中画出一个最大的圆，并求出圆的周长。对于这项实践性作业，根据已有的数学活动经验，绝大多数学生能正确画出草图（如图A），并能正确计算：c=3.14×5=15.7（cm）。教师反馈评讲后，又追问图中正方形周长是多少，学生同样给予正确解答：c=4×5=20（cm）。

【问题探讨】

应该说，教师在巩固知识阶段设计实践性作业，既能巩固所学知识又能促进学生的动手能力和空间观念的培养，值得称道。但本题所蕴涵的潜在的教学价值，该教师没有进行深度挖掘和有效利用：借助图与计算结果，学生可以根据数学活动经验，判断出圆的周长小于正方形的周长，再比较它们的算式，可以说明圆周率一定小于4。继而教师可以提出一个挑战性的任务：谁能设计一个问题解决方案——说明圆周率一定大于某数，就比如大于3，引发学生的积极思考和主动探究。其改进设想的教学价值有两点：一是改进设想其实体现了数学研究中的构造性思想，它是一种高认知的思维活动。即使学生无法达到设想要求，那也是值得肯定的，至少在教师的启发引导下，学生经历了这种高认知思维的过程。二是从设计活动所期望体现的结果看，足以展现猜测和估计活动对数学研究和探究活动的价值，能对圆的周长计算公式探究活动起到锦上添花之作用。同时对后面圆的面积计算公式的探究学习有着很好的启示。

图A

【教学重建】

该怎样开发和利用本题所蕴涵的教学价值？以及如何引导学生经历高认知的数学思维活动呢？教师首先可以结合图与算式，引导学生从比较中得出圆的周长小于正方形的周长，从而说明圆周率一定小于4。在此基础上教师提出一个挑战性的任务：谁能设计一个方案说明圆周率一定大于某数，就比如大于3，引导学生进行相关设计。学生受上面图示的启发以及自身的数学活动经验，可能提出这样的设想：

当然，图B-1和图B-2，用学生现有数学知识无法得出圆的直径与正三角形和正方形边的关系，因而学生无法解答与说明。对此，教师对其设计思路应给予肯定，不应作全盘否定，学生至少经历了数学思考和操作活动。图B-3则可用学生现有的知识和经验加以简要推理说明：圆的周长大于正六边形的周长。设圆的直径为d，圆周长=仔d；由于正六边形分割后的6个图形都是相同的等边三角形，边长为d，则正六边形的周长为3d。因而说明圆周率一定大于3。从中我们得出圆周率介于3～4之间。这样，通过构造图形从估算角度进一步验证圆周率的数值范围，引领学生体验数学探究与发现的一种常用思想和策略。这种构造性思想方法及其探究关系的分析、推理活动，对六年级学生来说无疑是高认知的思维活动。

总之，“数学教学是数学活动的教学”，重视教学过程的活动化设计，这是改善教与学方式的有效策略之一。加强动手操作活动是改进教学、提高教学有效性的重要策略。需指出的是，“数学操作活动”不是指单纯的肢体运动，而是指观察、实验、操作、归纳、类比、猜想、推理、验证、交流、反思等一系列的数学认识活动。数学思维应当是数学操作活动之“灵魂”。只有引导学生经历思维、经历发现、经历解决过程的实践操作和自主探究，才是有效的教学，学生才能成为真正的探究者。

[1]顾汝佐.不要让学生做“操作工”[J].小学数学教师，2001（9）.

[2]吴相会.合作学习中课程资源的有效运用[J].小学教学参考（数学版），2010（5）.

[3]李继军.从关注教学细节入手改进教学行为例谈[J].中小学教师培训，2009（5）.