变速多移动质量耦合作用下柔性梁系统振动响应分析
王颖泽,张小兵
(1.江苏大学 能源与动力工程学院,江苏 镇江 212013;2.南京理工大学 动力工程学院,南京 210094)
在车辆通过桥梁及弹丸飞离身管的过程中,车辆及弹丸的高速运动产生的惯性载荷将分别引起桥梁及身管的弹性振动,对桥梁的结构设计[1]及弹丸的射击精度[2]产生重大影响,为此对于此类移动质量作用下柔性梁的振动响应分析一直受到国内外学者的重视。对于此类问题的分析求解,由于涉及到移动质量的刚性运动与柔性梁弹性振动的耦合作用而变得十分复杂,特别是随着移动质量数目的增加且作变速运动时,移动质量之间的相互影响及加速度产生的动力学效应使得问题的求解更加困难。目前国内外对这类问题的研究主要集中在单个移动质量作用下柔性梁系统的振动响应分析,且大多是在不计移动质量的惯性效应或者移动速度为匀速的前提下进行分析求解的[3-8],对于全面考虑包括移动质量数目,运动形式,惯性效应,变速产生的Coriolis惯性力、离心惯性力及相对惯性力等因素在内的系统分析还很少见,其中文献[9,10]分别对单个移动质量作用下各种惯性效应对梁振动的影响进行了较为全面的分析。由于在工程实际中,同时作用于桥梁或者身管的移动质量往往不只一个[11],其相互间的耦合作用产生的振动效应不同于单个移动质量的作用效果,对梁整体的振动特性产生较大影响。为此本文结合柔性梁振动理论,在全面考虑各种因素影响的基础上,建立了多移动质量耦合作用下柔性梁系统的振动方程,通过数值求解对多移动质量以各种运动形式作用下柔性梁系统的振动特性进行系统分析,给出了多移动质量作用下柔性梁系统振动响应规律,为桥梁-车辆系统及身管-弹丸系统的整体设计及精度优化提供了必要的理论参考。
1 柔性梁系统振动方程
1.1 振动方程的建立

图1 多移动质量-梁系统振动模型Fig.1 Vibration model of the Multi-moving masses-beam
考虑如图1所示简支梁模型,其上作用质量为mi,速度为vi,加速度为ai的多个运动物体,令t时刻梁上x处的挠度为w(x,t),根据柔性梁振动理论可得多移动质量作用下梁的振动方程为:

式中:EI为梁的抗弯刚度,ρ为梁的单位长度质量密度,A为梁的截面积,δ为 Dirac函数,,,,分别为移动质量变速运动时产生的牵连惯性力、Coriolis力、向心力及相对惯性力。
1.2 振动方程的解耦
选取简支梁的振型函数为模态函数,采用模态叠加法对方程进行坐标变换,其变换形式为:

将式(2)代入式(1)进行模态展开:

上式两端分别乘以φk(x)并沿0到L积分,根据模态函数的正交性化简可得:

式中:

由此得到可数值求解的二阶时变微分方程组:

式中:

2 柔性梁振动响应分析
对于解耦获得的二阶时变微分方程组,采用降阶的方法将其转化为一阶代数-微分方程组,选取变步长四阶Runge_Kutta法进行数值求解可得到q(t)的分布规律,将其带入式(2)中即可获得w(x,t)的分布规律。
2.1 算例验证
为了验证本文求解模型的正确性,选取文献[12]提供的计算实例进行求解分析。相关的计算参数如表1所示。

表1 计算参数Tab.1 Calculation parameters
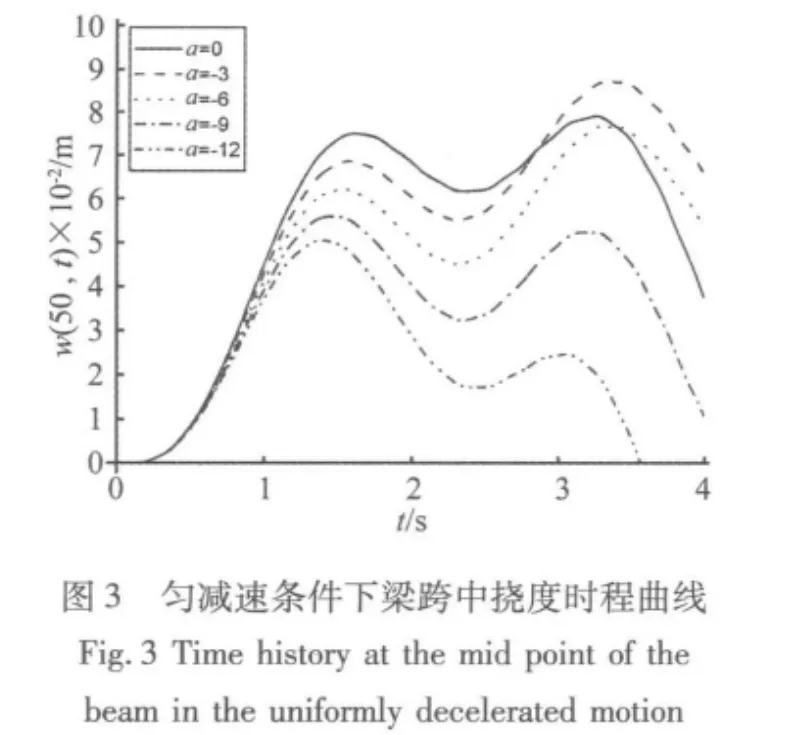
取移动质量数N=3,分别对初速为20 m/s条件下作匀加速和匀减速的情况计算求解得到如图(2)、图(3)所示结果,通过对比可知本文计算结果同文献[12]结果十分吻合,从而验证了本文计算模型的正确性。
2.2 柔性梁振动响应求解分析
由于移动质量数目的增多,其相互间运动形式也相应变得复杂,不失一般性文本选取两个移动质量分别对其在同向和相向运动条件下的变速运动进行分析,进而系统阐述柔性梁在多移动质量作用下的振动响应。
2.2.1 同向运动求解分析

选取移动质量mi=3.06×104kg,其他计算参数同上。分别对不同初速、不同加速度条件下的梁振动情况进行数值求解可得:
(1)从图4给出的不同初速条件下移动质量以相同加速度作匀变速运动时梁跨中处挠度的分布曲线中可以看到,在多移动质量作用下梁跨中处的挠度呈现波动现象,且挠度的振幅随着变速的形式和大小的不同而不同:当作匀加速运动时,挠度的最大峰值随着加速度的增大而增大,而作匀减速运动时,挠度的最大峰值随着加速度绝对值的增大而减小。通过与图2和图3对比可知,在多移动质量作同向运动时,梁跨中处的挠度分布规律同单移动质量作用下的挠度分布规律相似,但由于多个载荷相互间的影响使得挠度的波动性更加剧烈。
(2)从图5给出的加速度不同条件下移动质量以相同初速作变速运动时梁跨中处挠度的分布曲线中可以看到,当移动质量均作变速运动时,挠度的振幅随着初速的增大而增加,且最大幅值增加的幅度随着初速的增加而减小,随着初速的增大波动逐渐趋向等振幅波动。通过对比图5(a)和图5(b)可以看到,当移动质量间加速度同向与反向时,对梁跨中处挠度的影响随着速度的增大而逐渐减小。
(3)图6给出了初速不同条件下移动质量以相同加速度作匀变速运动时不同时刻梁挠度沿轴向的分布曲线。从图中可以看到,随着移动质量的不断向前运动,挠度的最大峰值点不断向移动质量前进的方向移动,且最大峰值并不是随着运动的进行而单调增大而是呈现先增后减的变化规律,究其原因是由于挠度是由弯矩产生的,而移动质量运动产生的弯矩并不是随着运动的进行而单调增大,因而呈现了挠度分布的波动效应。

图4 初速不同、加速度相同条件下梁跨中挠度分布曲线(v01=20 m/s,v02=40 m/s)Fig.4 Deflection at the mid piont of the beam in the different initial velocity and equal acceleration

图5 初速相同、加速度不同条件下梁跨中挠度分布曲线Fig.5 Deflection at the mid piont of the beam in the different acceleration and equal initial velocity

图6 初速不同、加速度相同条件下梁挠度轴向分布曲线(v01=20 m/s,v02=40 m/s)Fig.6 Axial distribution of the deflection of the beam in the different initial velocity and equal acceleration
2.2.2 相向运动求解分析
当移动质量分别以不同的初速或者不同的加速度相向运动时,由于其中一个运动方向与坐标轴反向,为了表述清晰,下面的分析中移动质量的速度及加速度均以各自前进的方向为正。
图7给出了移动质量分别以初速为20 m/s和40 m/s从梁的两端以相同的加速度变速运动时梁跨中处挠度分布曲线。通过对比图4可知,梁跨中处挠度在相向运动与同向运动情况下分布规律是一致的,究其原因是尽管移动质量之间运动形式的不同产生不同的弯矩,但是其合弯矩在跨中处是一致的,因此产生的挠度也是相同的。但是在其他位置处由于合弯矩的不同其挠度分布也相应的不同,为了能够明显体现运动形式不同对挠度的影响差别,图8给出了L/4处同向运动与相向运动时挠度差值随时间的分布曲线。从图中可以清楚地看到移动质量间运动形式的不同导致梁挠度分布产生较大的差异,其分布在运动开始阶段呈现剧烈的波动,随着运动的不断进行波动现象逐渐平缓趋于等振幅波动。通过对比图8(a)和图8(b)可以得到:当作加速运动时随着加速度值的增大挠度最大差异值不断增大;当作减速运动时随着加速度绝对值的增大挠度最大差异值不断减小,其变化规律同变速对挠度峰值的影响是一致的。
图9给出了移动质量分别以初速为20 m/s和40 m/s从梁的两端以相同的加速度变速运动时不同时刻梁挠度沿轴向的分布曲线。通过与图6对比可知,由于移动质量之间作相向运动导致挠度的最大峰值点在梁两端不同移动,这与同向运动时挠度的峰值点向移动质量前进的方向移动是相区别的。随着运动的进行挠度最大峰值依然呈现波动现象,这与同向运动时是相类似的。

图7 匀变速条件下梁跨中挠度分布曲线(v01=20 m/s,v02=40 m/s)Fig.7 Deflection at the mid point of the beam in the uniformly variable motion

图8 匀变速条件下梁L/4挠度差值分布曲线(v01=20 m/s,v02=40 m/s)Fig.8 Deflection at the L/4 of the beam in the uniformly variable motion

图9 匀变速条件下梁挠度沿轴向分布曲线(v01=20 m/s,v02=40 m/s)Fig.9 Axial distribution of the deflection of the beam in the uniformly variable motion
2.2.3 耦合影响分析
随着移动质量数目的增多,由于梁振动方程的非线性,移动质量运动对梁产生的整体振动效应并不是简单的线性叠加,其相互间的运动将影响各自对梁的作用效果。为了能够系统阐述相互间运动产生的耦合影响,本文分别计算了单个移动质量以初速为20 m/s和40 m/s,加速度值为3 m/s2作匀加速和匀加速运动时梁的振动响应,将得到的结果进行线性叠加与同向运动和相向运动条件下的计算结果进行对比分析可得:
(1)图10给出了不同运动形式下梁挠度沿轴向的分布曲线。从图中可以看到移动质量间的相互运动对梁振动产生的整体效应与单个移动质量作用的线性叠加在挠度的峰值、峰值点的位置都有差别,为了能够显著地突出多移动质量耦合作用与单个质量作用的线性叠加对梁振动的整体影响差别,将同向运动及相向运动得到的结果同线性叠加结果进行差值比较得到图11所示的梁挠度差值三维分布曲线,从中可以清楚地看到不同运动形式对梁振动的影响效果,其中同向运动的耦合效应在运动初始阶段并不明显而是到了运动的后半段才逐渐显现出来,而相对运动的耦合效应则在运动的整个过程中都很明显。
(2)图12给出了不同运动形式下梁挠度差值沿轴向的分布曲线。从图中可以看到初速及加速度的不同对移动质量间相互运动耦合效应的影响情况:同向运动时,移动质量间的相互影响随着加速度的增大而增加,随着初速的增加先减小后增大;相向运动时,移动质量间的相互影响随着加速度的增大而减小,随着初速的增加先减小后增大。



3 结论
本文以车辆过桥梁及弹丸飞离身管过程中,由于车辆及弹丸的变速运动对桥梁及身管产生的振动响应为工程背景,建立了多移动质量耦合作用下柔性梁振动响应模型,采用模态叠加法对模型进行解耦分析得到便于数值求解的二阶时变系统方程组,通过对不同运动形式下柔性梁振动响应的求解分析可得到以下结论:
(1)多移动质量运动形式的不同对梁的振动效果不同。在同向运动条件下,当多移动质量作变速运动时,梁各点处的挠度峰值随着移动质量初速、加速形式及大小的不同而不同:当作加速运动时,各点处挠度峰值随着加速度值的增大而增大;当作减速运动时,各点处挠度峰值随着加速度绝对值的增大而减小;当移动质量初速变化时,各点处挠度的峰值随着初速的增大而增大,但增大的幅度随着初速的增大而减小。在相向运动条件下,其对梁的振动效应与同向运动相似,只是幅度有所不同。
(2)多移动质量共同作用下相互间的运动会影响各自对梁的作用效果,其耦合作用随着相互间运动形式的不同而不同:多移动质量同时作用时其对梁的整体振动效应要大于单个移动质量作用的叠加效果;同向运动时,多移动质量相互间的耦合作用随着加速度的增大而增大,随着初速的增大先减小后增大;相向运动时,多移动质量相互间的耦合作用随着加速度的增大而减小,随着初速的增大先减小后增大。
[1]陈上有,夏 禾,战家旺,等.变速移动荷载作用下简支梁的动力响应分析[J].中国铁道科学,2007,28(6):41-46.
[2]彭 献,张 普,刘子建.基座运动情况下弹炮系统的振动分析[J].振动与冲击,2009,28(3):23 -26,58.
[3]Ichikawa M,Miyakawa Y,Matsuda A.Vibration analysis of the continuous beam subjected to a moving mass[J].Journal of Sound and Vibration,2000,230(3):493 -506.
[4]Michaltsos G T.The influence of centripetal and coriolis forces on the dynamic response of light bridges under moving vehicles [J].Journal of Sound and Vibration,2001,247(2):261-277.
[5]Michaltsos G T.Dynamic behaviour of a single-span beam subjected to loads moving with variable speeds[J].Jounral of Sound and Vibration,2002,258(2):359 -372.
[6]Wu J J.Dynamic analysis of an inclined beam due to moving loads.Journal of Sound and Vibration,2005,288(1 -2):107-131.
[7]何万龙,任伟新,吴建基.柔性梁上高速移动质量动力响应分析[J].振动与冲击,1998,17(1):67-74.
[8]Yau J D,Yang Y B.Vertical accelerations of simple beams due to successive loads traveling at resonant speeds[J].Journal of Sound and Vibration,2006,289(1 - 2):210-228.
[9]Yau J D,Fr ba L.Response of suspended beams due to moving loads and vertical seismic ground excitations[J].Engineering Structures,2007,29(12):3255 -3262.
[10]姜 末.移动质量载荷在梁中激起的振动[J].力学与实践,2002,24(6):44 -47.
[11]王颖泽,张小兵,袁亚雄.基于膨胀波新发射机理的身管振动响应分析[J].振动与冲击,2009,28(8):144 -148.
[12]彭 献,刘子建,洪家旺.匀变速移动质量与简支梁耦合系统的振动分析[J].工程力学,2006,23(6):25-29.

