含运动副间隙的轮转机刀式折页机构的动态响应特性

袁英才 ，刘义伦，王仪明

(1. 中南大学 机电工程学院，湖南长沙，410083；2. 北京印刷学院 机电系，北京，102600)

由于相接触两构件产生相对运动，装配、制造误差以及在运转过程中产生磨损，因而，在机械系统中运动副产生间隙不可避免。在低速状态下，运动副间隙对机械系统的影响可以忽略。但是，在高速状态下，虽然运动副间隙对机械的运动轨迹影响很小，但其对机械的动力精度和机械动力学性能有重要影响，会产生冲击载荷，引起机械振动和噪声[1]。国内外研究者对由运动副间隙产生的机械系统非线性振动现象进行了大量研究，如：Dubowsky等[2]对含间隙机械系统进行了动力学分析；Morita等[3-5]对含间隙四杆机构动力学及混沌现象进行了研究，Bauchau等[6-7]对多体机械系统中运动副间隙进行了建模分析；Chen等[8-9]对运动副间隙进行了非线性动力学分析；常宗瑜等[10-11]对运动副间隙引起的混沌现象及其稳定性进行了研究；郭鹏飞等[12-13]对含间隙机构的运动精度和误差进行了研究。轮转机是印刷机械中运行速度最高的大型设备，在书刊、报纸的印刷中应用广泛。轮转机的折页系统在高速状态下，由运动副间隙引起的非线性振动现象对折页的精度影响十分明显，严重制约轮转机的印刷速度。目前，国内对刀式折页机构的动态特性分析都是以理想转动副有前提进行的[14-15]，没有考虑运动副间隙的影响，因此，有必要定量研究运动副间隙对轮转机刀式折页机构动态特性的影响。

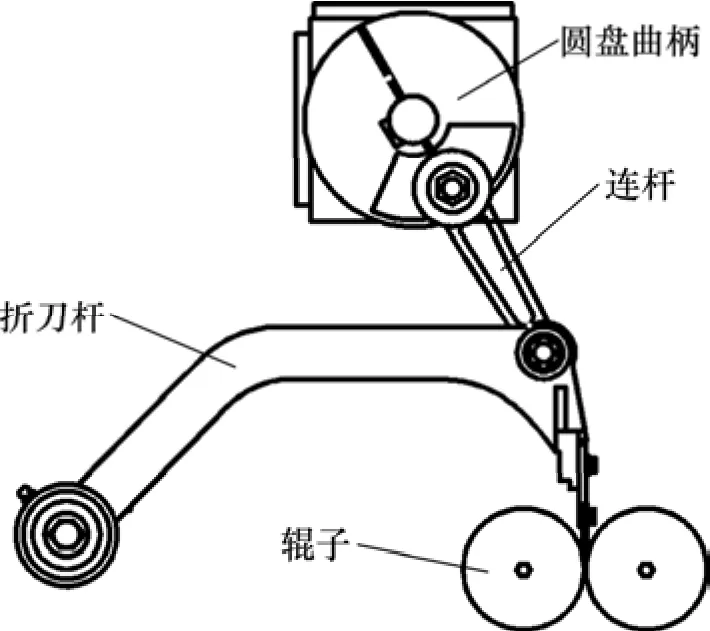
图1 刀式折页机构Fig.1 Folder mechanism

图2 折页机构运动简图Fig.2 Kinematic sketch of fold mechanism

1 轮转机刀式折页机构运动学分析

轮转机刀式折页机构基本结构如图1所示，它是通过刀头进入两辊子之间，完成纸张的折页动作。为分析运动副间隙，建立刀式折页机构运动简图及坐标系，如图2所示，各杆长分别为l1，l2，l3，l4和l5。折刀装在杆5上，折刀杆由杆5与杆4固接在一起形成，其夹角为β，质量为m4，转动惯量为JS4，质心距端点距离为ls4。连杆与曲柄的质量分别为m2和m3，转动惯量分别为JS2和JS3；质心距端点距离分别为ls2和ls3。曲柄、摇杆、折刀杆与x轴的夹角分别为θ2，θ3和 θ4；质心的坐标为(xs2，ys2)，(xs3，ys3)，(xs4，ys4)。

运动副间隙很小，且有阻尼存在，销与轴套之间分离和碰撞时间很短，因而，可以认为组成运动副的销轴与轴套之间保持连续接触，采用连续接触假设，即将间隙假设成长度等于间隙量的无质量刚性杆。若r1， r2，r3和 r4为各运动副间隙，α1，α2，α3和 α4为各间隙角，则折页机构变成八杆机构，有5个自由度。采用曲柄转角 θ2和间隙角 α1，α2，α3和 α4这 5 个运动参数作为广义坐标，则 θ3和 θ4是广义坐标 q=(θ2，α1，α2，α3，α4)的函数。各杆转角关系如图1所示，折页机构向x和y轴方向上投影，可得其运动关系方程：

将式(2)代入式(1)中第2式，可得：

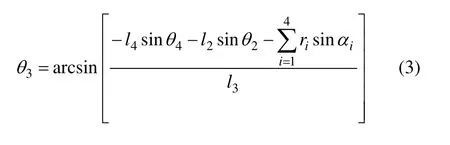
θ3和 θ4是 θ2，α1，α2，α3和 α4的函数，将其对时间求导可得角速度和角加速度：

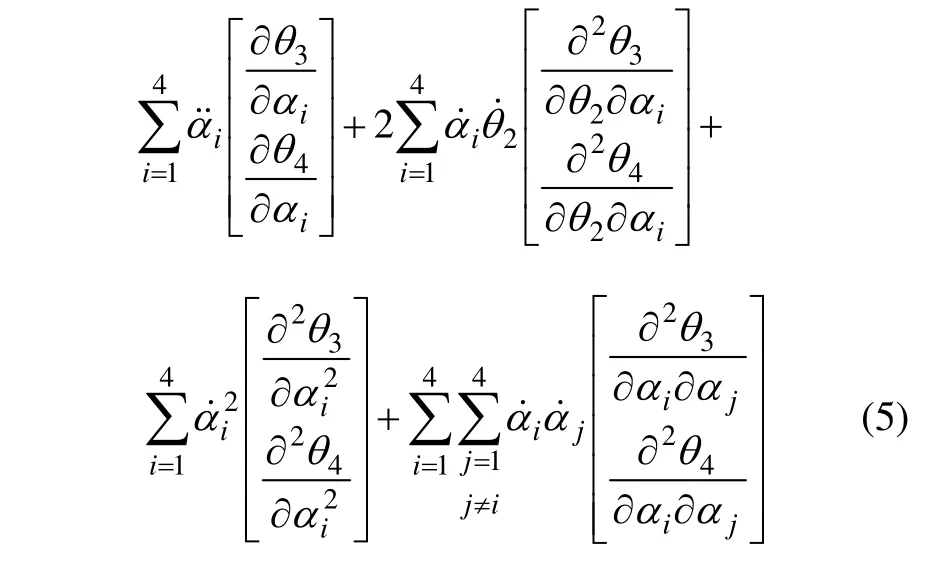
2 动力学分析

采用耗散函数的拉格朗日方程式，对折页机构建立如下动力学方程：

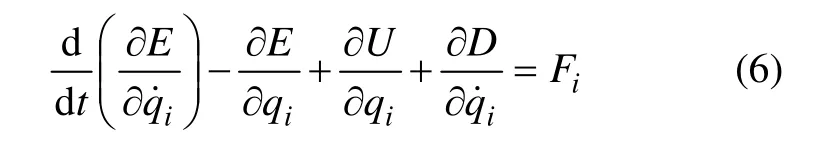
式中：qi为广义坐标，即qi=[θ2,α1,α2,α3,α4]；E，U和D分别为系统的动能、势能和耗散能；Fi为广义外力。动能、势能和耗散能分别为：

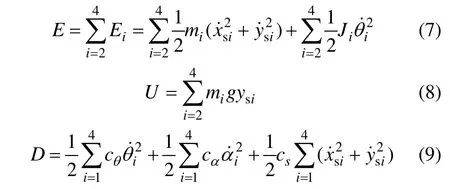
式中：cθ为转角阻尼系数；cα为间隙角阻尼系数；cs为线位移阻尼系数。

折页机构曲柄转速θ˙2在工作状态下恒定，即=ω2，则θ2= ω2t 。对运动副间隙接触角 α1，α2，α3和α4，各广义坐标的动力学方程可以写为：

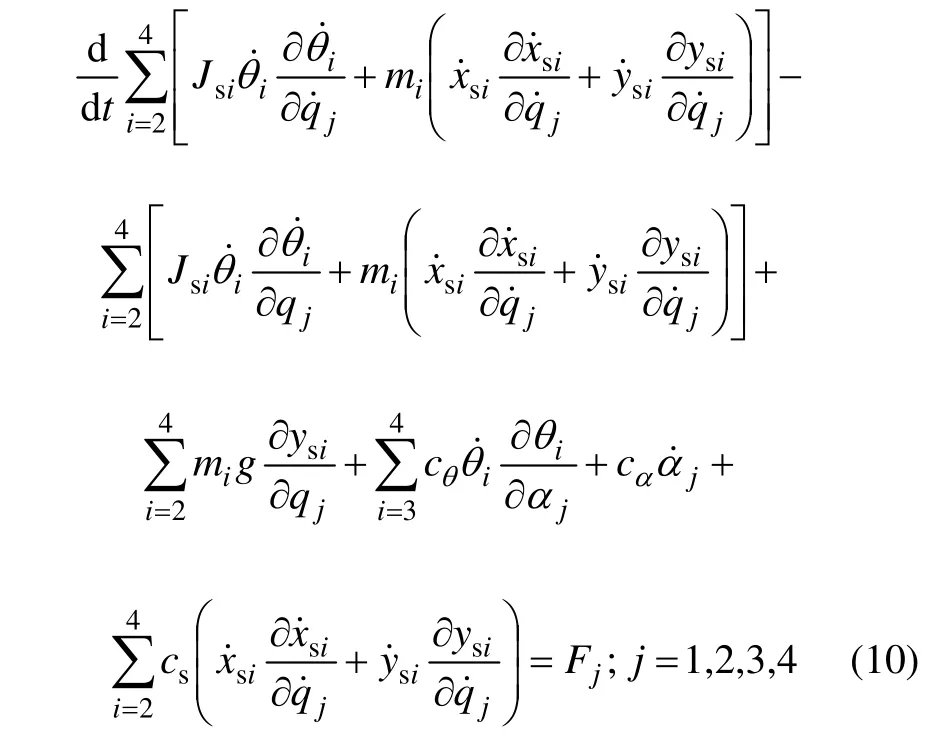
式(10)简化为：

式(11)为二阶偏微分非线性方程组，可以用数值解法求出各间隙角的角加速度和，进而求出和。由式(2)~(5)可求出折刀的角位移、角速度和角加速度。

3 刀式折页机构动态特性分析

某刀式折页机构的结构参数如表1所示。在转速为28 800 r/h，运动副间隙为0.2 mm，阻尼系数cθ=0.1 N·s/rad，cα=0.1 N·s/rad，忽略 cs时，折刀的加速度动态响应曲线如图3所示。从图3可见：由于考虑运动副间隙，销轴与轴套之间发生了碰撞，使折刀的加速度动态响应表现出明显的非线性特征。

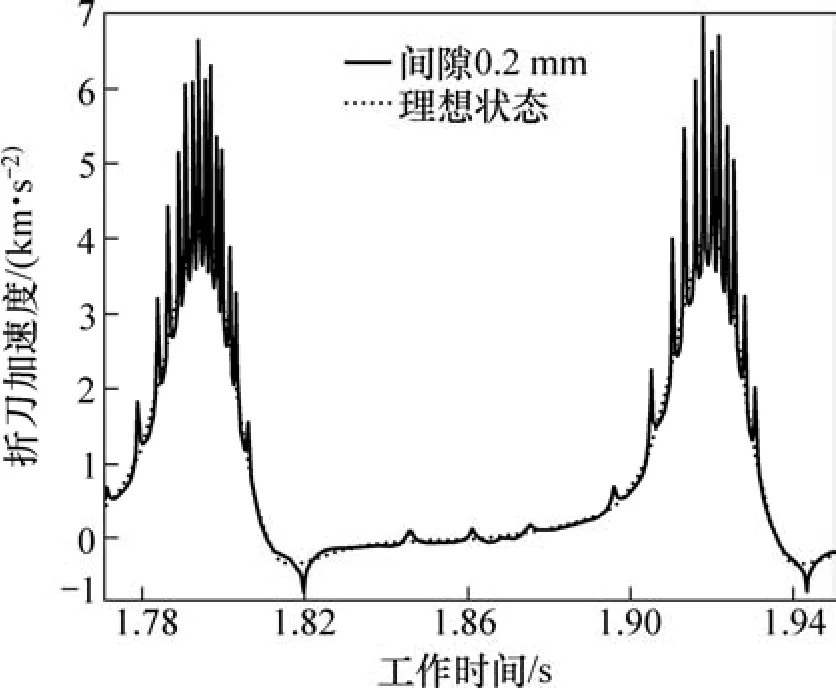
图3 加速度动态响应曲线Fig.3 Acceleration curves of dynamic response

为了进一步研究运动副间隙对折刀动态响应特性的影响，模拟了不同转速、不同运动副间隙条件下，折刀加速度动态响应的情况。在各种运动副间隙状态下，折刀加速度峰值随机构运动速度变化如图4所示。从图4可见：折刀的加速度随着曲柄转速上升呈非线性增长。在转速小于10 000 r/h时，运动副间隙对折刀加速度影响很小，但是，随着转速上升，运动副间隙量对折刀加速度峰值的影响非常显著。这种加速度的急剧上升和变化引起折刀出现强烈振动现象，从而影响了折页的精度。为了更好地反映刀式折页机构的加速度动态响应特性，引入冲击动载系数Kd。Kd为加速度动态响应曲线中加速度最大的5个峰值的平均值与理想状态下加速度的峰值之比。冲击动载系数 Kd见表2。由表2可见：刀式折页机构的冲击动载系数并不完全随着曲柄转速的上升而增大，存在一定的波动性，但是，动载系数随着运动副间隙r增大而显著上升；当运动副间隙为 0.01 mm时，Kd基本稳定在1.100 0左右，刀式折页机构能够很好地运转；当运动副间隙量达到0.10 mm时，Kd在1.400 0~1.500 0之间波动，此时，折页机构随着曲柄转速的上升，折刀的非线性动态特性比较明显；当折页机构运动速度达到32 400 r/h时，折刀的加速度峰值达7.0 km/s2，折页机构的稳定性无法保证，已不能达到折页精度的要求；当运动副间隙为0.20 mm时，Kd在1.700 0~2.100 0之间波动，为保证折页精度，机构的运转速度只能在28 000 r/h以下；此外，刀式折页机构必须进行维修。

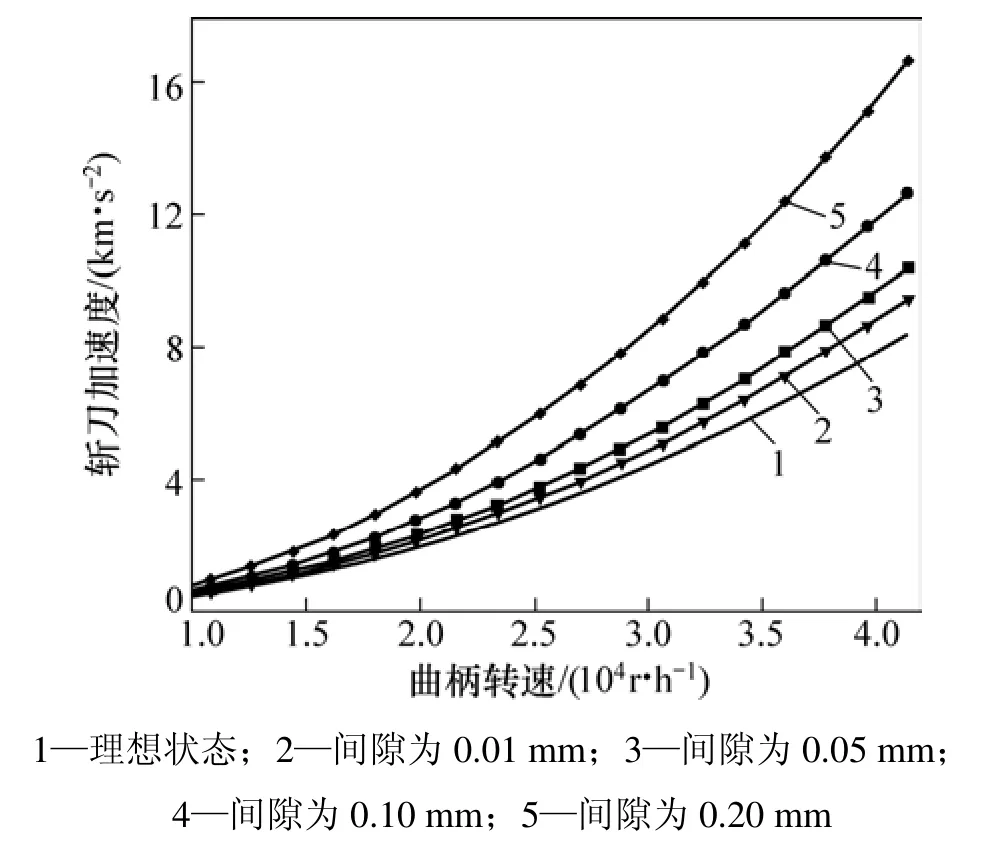
图4 加速度峰值曲线Fig.4 Peak acceleration curves

表1 刀式折页机构主要结构参数Table1 Main structural parameters of fold mechanism

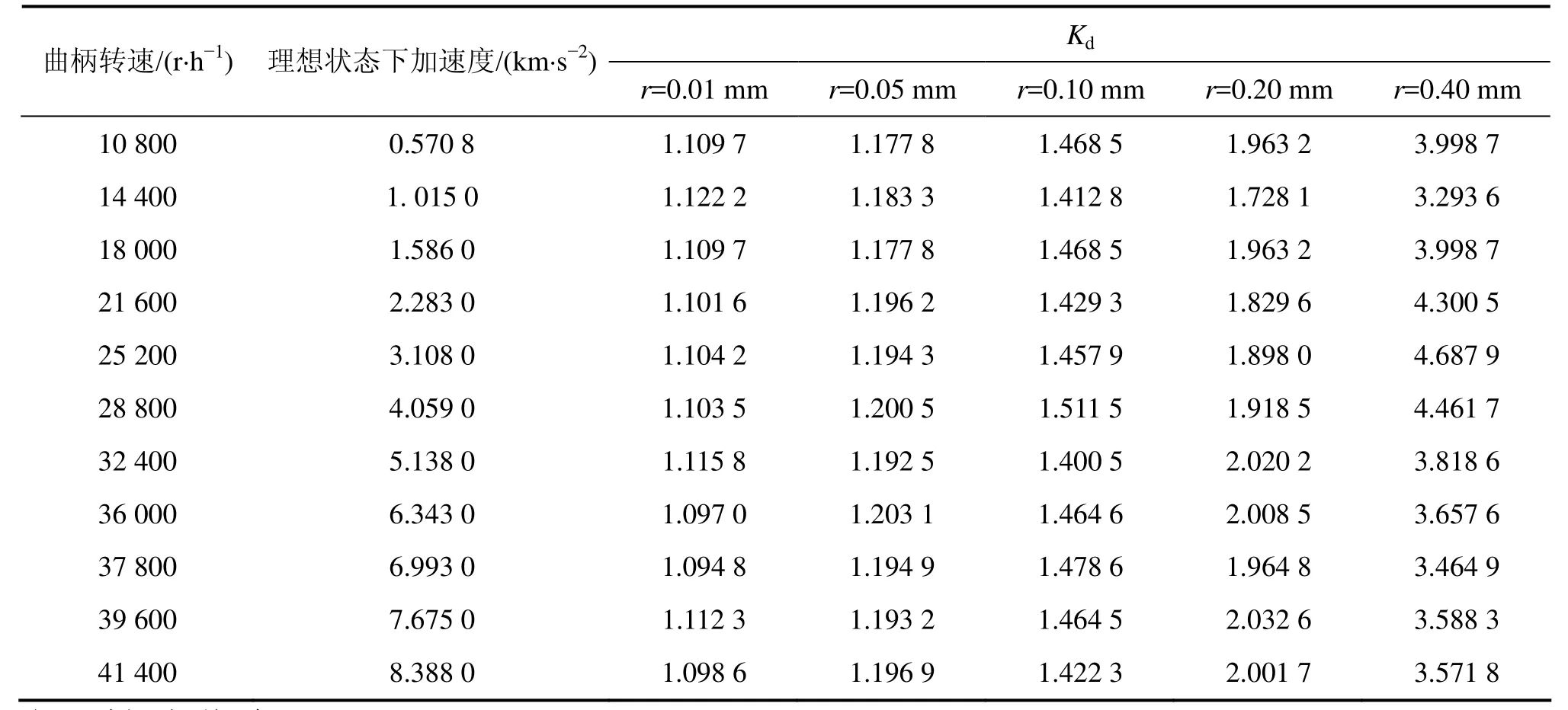
表2 冲击动载系数KdTable2 Impact dynamic load coefficients Kd

4 结论

(1) 在高速状态下，由于运动副间隙的存在，轮转机刀式折页机构动态响应表现出明显的非线性特征，机构运转的平稳性和精度将随之下降。

(2) 运动副间隙量是影响轮转机刀式折页机构动态特性的关键因素。当折页机构运动副间隙达到 0.1 mm以上时，机构的非线性动态特性十分明显，机构的冲击振动现象加剧，折页精度下降。因此，为了保证轮转机刀式折页机折页的精度和运转平稳性，在进行设计和装配时，要严格控制各运动副间隙；在使用过程中，要使机构处于良好润滑状态，防止运动副过快磨损，造成机构精度下降，运动副间隙扩大。

[1] 杨义勇, 金德闻. 机械系统动力学[M]. 北京: 清华大学出版社, 2009: 210-211.

YANG Yi-yong, JIN De-wen. Mechanical system dynamics[M].Beijing: Tsinghua University Press, 2009: 210-211.

[2] Dubowsky S, Freudenstein F. Dynamic analysis of mechanical systems with clearances. Part I and II[J]. Journal of Engineering for Industry, 1987, 93(13): 305-316.

[3] Morita N, Furuhashi T. Research on Dynamics of four-bar linkage with clearances at turning pairs[J]. Bulletin of the JSME,1978, 158(21): 1292-1298.

[4] Grant S J, Fawcett J N. Effects of clearance at coupler-rocker bearing of 4-bar linkage[J].Mechanism and Machine Theory,1979, 14(3): 99-110.

[5] Seneviratne L D, Earles S W. Chaotic behavior exhibited during contactless in clearance joint of four-bar mechanism[J]. Machine and Material Technology, 1992, 178(3): 307-321.

[6] Bauchau O A, Rodriguez J. Modeling of joints with clearance in flexible multibody systems[J]. International Journal of Solids and Structures, 2002, 39(3): 41-63.

[7] Flores P, Ambrósio J. Revolute joints with clearance in multibody systems[J]. Computers and Structures, 2004, 82(6):1359-1369.

[8] CHEN Yu-shu, MENG Quan. Bifurcation in nonlinear rotor-bearing system[J]. Journal of Vibration Engineering, 1995,15(3): 266-275.

[9] 李哲. 考虑运动副间隙和构件弹性的平面连杆机构动力学研究[D]. 北京: 北京工业大学机械工程学院, 1991: 21-50.

LI Zhe. Dynamic research of the planar linkage thinking about the pair clearances and component elasticity[D]. Beijing: Beijing University of Technology. Department of Mechanical Engineering, 1991: 21-50.

[10] 常宗瑜, 王玉新, 张策, 等. 含间隙机构中的混沌现象[J]. 机械科学与技术, 1998, 17(3): 345-347.

CHANG Zong-yu, WANG Yu-xin, ZHANG Ce, et al. Chaotic behavior in Linkage with a clearance[J]. Mechanical Science And Technology, 1998, 17(3): 345-347.

[11] 常宗瑜, 张策. 含间隙机械系统的稳定性分析[J]. 机械科学与技术, 2000, 19(1): 4-5.

CHANG Zong-yu, ZHANG Ce. Stability analysis on mechanical system with clearance[J]. Mechanical Science And Technology,2000, 19(1): 4-5.

[12] 郭鹏飞, 阎绍泽. 含间隙四连杆机构运动误差的Monte Carlo模拟[J]. 清华大学学报: 自然科学版, 2007, 47(11): 1989-1993.

GUO Peng-fei, YAN Shao-ze. Monte Carlo simulation of motion errors for four-bar linkage with clearances[J]. Journal of Tsinghua University: Science and Technology, 2007, 47(11):1989-1993.

[13] 程强, 师忠秀, 杨倩. 含间隙平面连杆机构的运动精度概率分析[J]. 青岛大学学报, 2005, 20(2): 67-70.

CHENG Qiang, SHI Zhong-xiu, YANG Qian. Kinetic accuracy analysis for planar four-bar linkage with multiple clearances at turning pairs[J]. Journal of Qingdao University, 2005, 20(2):67-70.

[14] 王轶平, 李艳, 臧勇. 轮转机刀式折页机构优化研究[J]. 机械设计与研究, 2006, 22(6): 112-115.

WANG Yi-ping, LI Yan, ZANG Yong. Study and optimization of web press fold mechanism[J]. Machine Design and Research,2006, 22(6): 112-115.

[15] 施向东, 卢能才. 基于 ADAMS的十六开折页机构优化设计[J]. 包装工程, 2006, 27(6): 175-179.

SHI Xiang-dong, LU Neng-cai. Optimization design of the 16K folders based on ADAMS[J]. Packing Engineering, 2006, 27(6):175-179.