一种三滑块驱动平面并联手及其工作空间与位移特性分析

沈惠平 王 玮 邓嘉鸣 骆敏舟 马正华 杨廷力

1.常州大学,常州,213016 2.常州先进制造技术研究所,常州,213164

0 引言

大型工件数控加工时,往往由于刀具的运动范围较小而需要借助于工作台来改变大型工件的位置和姿态,以提高生产效率和加工精度。另外,若要在一般输送设备的输送过程中用人工改变被输送物的姿态,不仅费力,且不能保证每次操作的准确性;而采用机械手,将增加生产线的复杂程度及成本。若使用一种输送装置,在完成长、短距离输送的同时,能改变被输送物的姿态,则能更好地满足生产的需要。

此外,在线检测 LCD液晶面板、太阳能模组等大幅面光电产品的表面缺陷,必须从不同的方位和角度,辅以灯光照明才能检出,若能选择一种能改变位置和姿态的机构用于光电产品的检测,则可实现检测的自动化。

并联机构与串联机构相比,由于其具有刚度大、结构稳定、承载能力大、微动精度高、运动负荷小等优点,目前已在诸多领域开始得到广泛应用并成为机构学研究的热点之一。近年来,三自由度并联机器人也成为了研究的重点：Arakelian等[1]通过对对称型平面3-RRR三自由度并联机构动力学模型的研究,使作用在机架上的力和力矩为零;Gao等[2]给出了对称型平面3-RRR三自由度并联机构的工作空间形状和构件尺寸之间的关系;Kucuk[3]运用遗传算法对7种平面二支链三自由度并联机构的灵巧度进行分析比较,分析了一种灵巧度最优的构型;韩旭炤等[4]提出了一种非对称型平面三导轨3-PRR并联机构,对其进行了奇异性分析和工作空间分析;钱永明等[5]提出了一种同一导轨2-PRR+RPR平面并联机构,并将其应用于平面虚拟轴机床;杨建新等[6]在一种非对称二导轨3-PRR平面非冗余并联机构的基础上,对三种冗余并联机构的驱动奇异性进行了分析。

本文提出并研究一种非对称型三滑块分布在两个平行导轨上的三自由度平面并联机构[7],它与文献[6]介绍的3-PRR非冗余并联机构的不同之处在于,该机构包含的五杆单回路机构中的二滑块位于同一导轨上或同一铅垂面内的二个导轨上,工作空间更大。当三滑块沿平行导轨分别作往复直线运动时,工作台可改变位置和姿态,可广泛用于数控加工或操作时工件不同位姿的精确定位。

1 机构创新设计与运动学模型

1.1 机构创新设计

本文提出并设计的三滑块平面型并联数控操作平台如图 1所示,它包括三个滑块A、B、C,三个连杆1、2、3,以及工件板4。工件板4的两端分别以转动副D连接连杆3的一端,以复合转动副E连接连杆1、2的一端,而连杆1、2、3的另一端分别以转动副连接导轨1(K′)的滑块A、B和导轨2(K)上的滑块C,导轨 K、K′平行。易知,该机构自由度为3,且结构简单、制造容易、定位精度高。

图1 三自由度并联操作平台简图

1.2 运动学正解

建立直角坐标系Oxy,如图1所示,其中,A、B、C、D、E分别表示机构中的5个铰链;Si(i=1,2,3)分别表示三滑块A、B、C在导轨上的x方向的位移;设P(xP、yP)为末端执行平台4的中点位置,θ表示其与x轴正向夹角,Li(i=1,2,3)分别为1、2、3杆的杆长,L为执行平台4的长度;设θi(i=1,2,3)分别表示连杆1、2、3与x轴正向夹角;H表示两平行导轨之间的距离。

已知 S1、S2、S3,求执行平台 4的位姿(xP,yP,θ)。

由矢量法,易知机构运动学矢量方程：

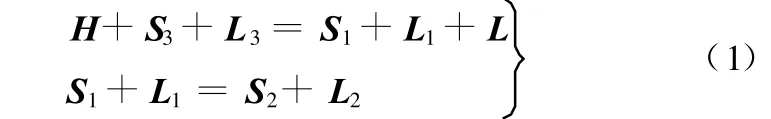
分别向 x轴、y轴投影,即有

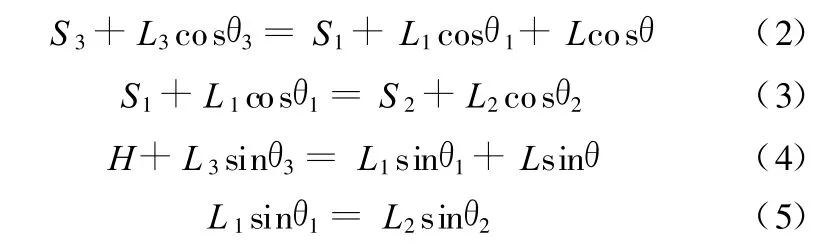
由式(3)、式(5)消去θ2,并化简得

由式(3)、式(5)消去θ1,并化简得

由式(2)、式(4)消去θ,并化简得

由上式可知,末端执行器 P的位置(xP,yP)及姿态θ均与滑块A 、B、C的位移S1、S2、S3有关,因此,该机构为非解耦。

1.3 运动学反解

已知平台 4 的位姿(xP,yP,θ),求 S1、S2、S3。由式(12)得

将式(14)代入式(5)得

将式(14)代入式(4)得

由式(11)得

由位置方程(式(17))对时间进行一次求导,即可得到速度反解方程：

2 工作空间分析

2.1 某种位置下摆角θ的最大变化范围

如图2所示,当连杆1、2拉直共线时,转动副E落在导轨上,此时滑块C左右移动时,对应工作台4呈现不同的姿态,工作台4在图2b和图2e状态下与x轴正向夹角分别呈现最大和最小值,则工作台4的最大摆角为

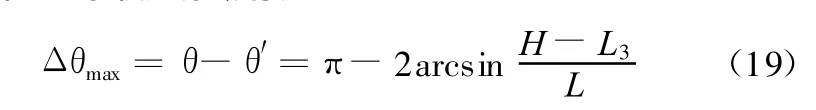
式(19)表明,H减小,L、L3增大可增大工作台4的摆角范围。

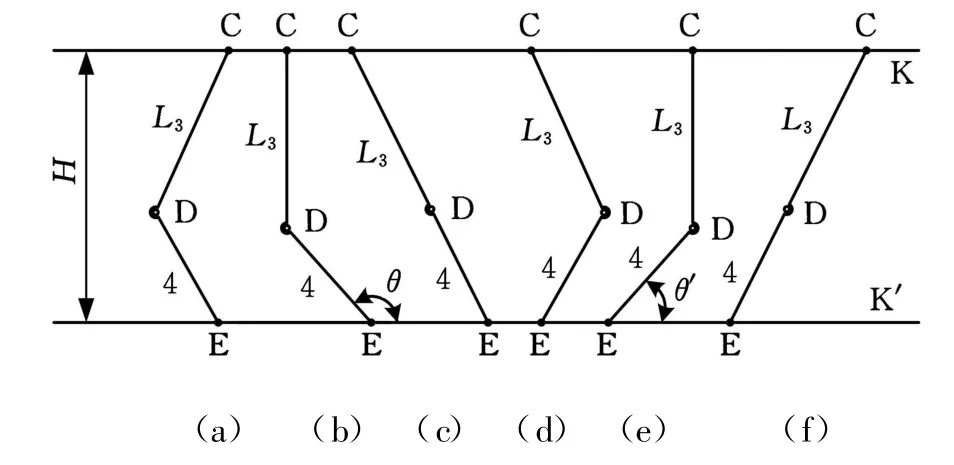
图2 L1、L2与水平导轨重合时,工作台4的不同姿态

如图3所示,若L1＜L 2,且不与水平导轨重合,当连杆1、2其中较短的一根杆垂直于导轨时,此时滑块C左右移动,对应工作台4呈现不同的位姿,显然,当连杆1垂直于平行导轨时,对应工作台4在图3b和图3f状态下与 x轴正向夹角分别呈现最大和最小值,这里讨论L1+L3＞H的情况,工作台4的最大摆角为

式(20)表明,H、L减小,L1、L 3增大可增大工作台4的摆角。

本文实验装置取连杆1、2的杆长L1=L2=500mm,平台4的长度 L=500mm,H=1000mm,在 L3的长度由 500mm逐渐变化到1000mm的过程中,对应工作台4的最大摆角如图4所示。

图3 L1＜L2时工作台4的不同姿态

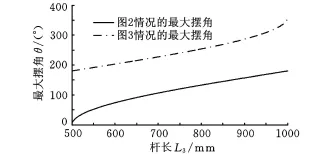
图4 L3取不同值时对应的最大摆角

2.2 某种姿态下位置(x,y)的最大变化范围

为了分析方便,仅以L1=L2=L 3=L 0的情况进行讨论,工作台4与x轴的正方向的夹角θ不变,L K为导轨长度,讨论工作台的中点P的工作空间。

图5c所示的状态下,L 0取得最大值,L max=H-L sinθ,此时,P点也无法作上下运动,仅能沿着导轨的水平方向作直线移动。

如图6所示,当杆长L 0满足L min＜L0＜L mid时,P点的工作空间S1=(L 0-L0 cosα)(L KL0 sinα-L cosθ),其中,α=arccos[(H-L sinθ-L0)/L0]。

如图7所示,当杆长L0满足L mid＜L0＜L max时,P点的工作空间S2=(L0-L 0sinβ)(L KL cosθ+L0sinα),其中,β为滑块C 位于最左端时L3与导轨的夹角。

由图6、图7比较可得,当L mid＜L0＜L max时,P点的工作空间较大。

图5 杆长的极限状态

图6 L min＜L0＜L mid时P点的工作空间

图7 L mid＜L 0＜L max时 P点的工作空间

3 应用实例研究及样机研制

现以图1所示的机构操作点P匀速行走,实现如图8所示的由直线、圆等构成的组合工艺曲线(曲线上的一些特征点的坐标已在图中标出),则所需三滑块的位移曲线规律如图9所示。

图8 曲线轨迹

该三自由度平面并联操作手的虚拟样机如图10所示,物理样机正在研制中。

4 结论

(1)发明并研究了一种三滑块驱动的平面并联机构,该机构结构简单、制造成本低、定位精度高、操作方便、具有解析的运动学正反解,易于实现实时控制,可应用于数控加工、变姿态运输、光电产品检测等需要变姿态的工业操作场合。

图9 三滑块位移变化规律

图10 并联操作手的虚拟样机

(2)推导了该机构运动学正反解解析公式,分析了该机构的工作空间,即在给定位置时工作台的最大转角和给定姿态时末端执行器的最大工作范围。

(3)运用MATLAB仿真分析了工作台在给定姿态的情况下,末端操作点沿给定组合曲线运动时,三滑块所应有的位置的变化规律,也给出了该三自由度并联操作手的虚拟样机,为其精确控制、设计制造奠定了基础。

(4)若在末端执行器上加Z方向的直线移动或A、B轴转动,即可构成四、五、六轴操作手,因此,本装置可应用于平面或空间的数控加工、工件运输、产品检验等。

[1] Arakelian V H,Smith M R.Design of Planar 3-DOF 3-RRR Reactionless Parallel Manipulators[J].Mechatronics,2008,18(10)：601-606.

[2] Gao Feng,Liu Xinjun,Chen Xu.The Relationships Between the Shapes of the Workspaces and the Link Lengths of 3-DOF Symmetrical Planar Parallel Manipulators[J].Mechanism and Machine Theory,2001,36(2)：205-220.

[3] Kucuk S.A Dexterity Comparison for 3-DOF Planar Parallel Manipulators with Two Kinematic Chains Using Genetic Algorithms[J].Mechatronics,2009,19(6)：868-877.

[4] 韩旭炤,黄玉美,陈纯,等.一种新型三自由度平面并联机构的运动学解析[J].西安理工大学学报,2009,25(1)：23-27.

[5] 钱永明,曹清林.一种三自由度平面并联机构的分析[J].机械设计与制造工程,2001,30(6)：29-33.

[6] 杨建新,余跃庆.平面三自由度冗余并联机构的驱动奇异性分析[J].中国机械工程,2006,17(6)：629-632.

[7] 沈惠平,李菊,王玮,等.一种三滑块平面型并联数控操作平台：中国,201010256966.3[P].2010-08