有均匀平均流的圆环管道声模态及其应用

柳占新 黄其柏

1.华中科技大学数字制造装备与技术国家重点实验室,武汉,430074 2.中国船舶重工集团710研究所,宜昌,443003

0 引言

气动声学是一门研究气体运动产生声音以及声音在运动气体中的传播过程的一门科学。由于气动声学方程复杂,要解析地描述复杂几何形体的气动声学场(包括声的辐射与传播)几乎是一件不可能的事。计算气动声学(computational aeroacoustics,CAA)的出现为打开气动声学的神秘大门提供了神奇的钥匙。一些简单几何形体的气动声学问题,相对较容易求出解析解或者进行实验验证,这类问题对验证CAA方法的准确性提供了素材,如CAA的一系列基准问题[1]。有平均流的圆环管道中的声传播问题就属于这类相对简单的问题,引起了大量学者的兴趣[2-5]。有平均流的圆环管道中的声传播的研究意义不仅在于给CAA提供论据,更重要的是它为研究更复杂的问题提供了思路。如人们用圆(环)管道近似代替涡扇发动机进气道,然后研究吸声材料添加方法[4,6-8]。本文将由线性欧拉方程出发,推导有均匀平均流的情况下圆环管道内的声传播、声功率的解析表达式,利用单个声模态来模拟涡扇发动机进气道的声传播现象。

1 有平均流的管道声模态

圆环管道的模型如图1所示,假定其轴向无限长,内外径分别为D i和D o,管壁都是刚性硬壁,管道内的平均流场均匀,其马赫数为Ma。对于圆环管道,自然坐标应该选用柱坐标,本文以(x,r,φ)代表柱坐标在轴向、径向和旋转方向上的分量。管道内声波的控制方程为线性欧拉方程,表述为

式中,ρ、u、v、w、p分别为流体(气体)的密度、x方向速度、r方向速度、φ方向速度、压力;γ为气体绝热指数;撇号“′”表示声学扰动量,上横线表示平均流。

图1 固壁圆环管道模型示意图

为了便于计算,所有变量都采用以下基准进行量纲一处理：长度基准为管壁外径D(即图1中的D o);速度基准为管道中的音速a0;密度基准为管道中空气密度 ρ0。时间为D/a0,故压力为 ρ0a20。

量纲一处理后,管道的外径为1。用σ代表圆环管道内外径之比,即σ=D i/D o,从而管道的内径Di=σ。所以管道外半径Ro=1/2,内半径Ri=σ/2。

由等熵关系知

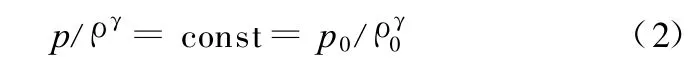
式(2)可以改写为

将p看成是ρ的函数,然后式(3)两边同时对ρ求导可得

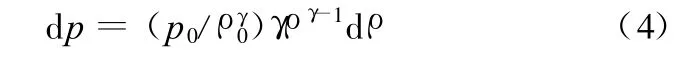
由于d p和dρ表示密度变化的小量——声学扰动量,所以 p′=d p,ρ′=dρ。同时 ,

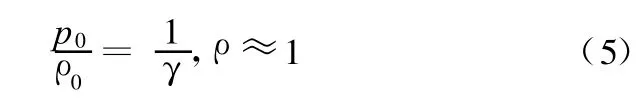
将式(5)代入式(4),可得

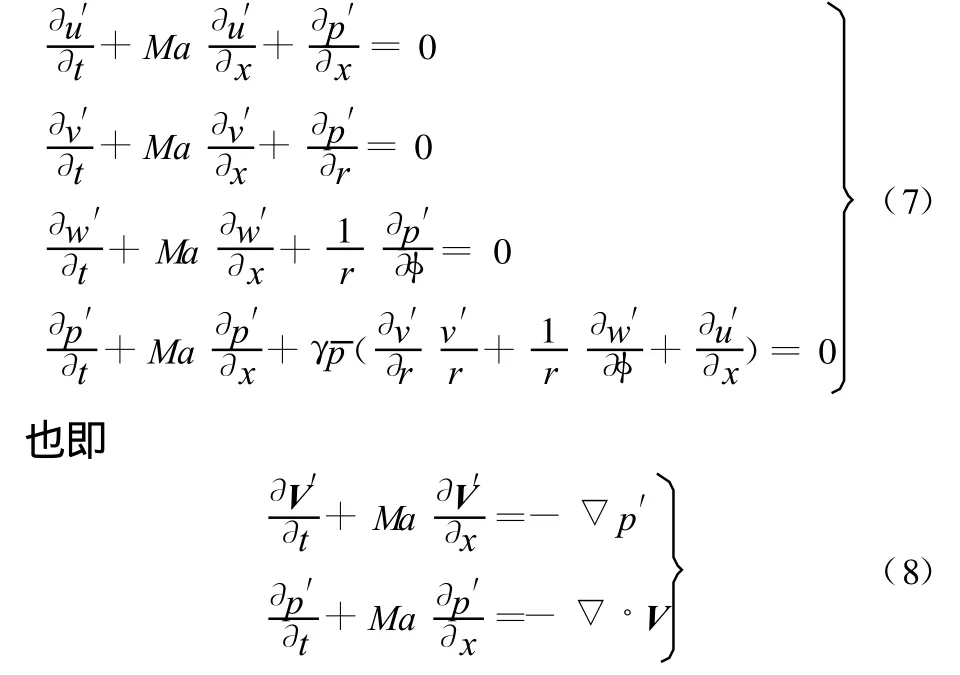
其中V=(u,v,w)为速度矢量。消去式(8)中的速度矢量,可得

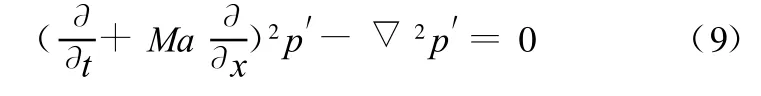
或者展开写成

式(9)或式(10)就是有平均流的情况下圆环管道的声传播控制方程。为了得到式(10)的解,还需添加适当的边界条件。对于刚性壁,应该添加无穿透边界条件,即

对于圆环管道里传播的声音,可以认为其由很多个Fourier模态组成,而单个Fourier模态的形式为

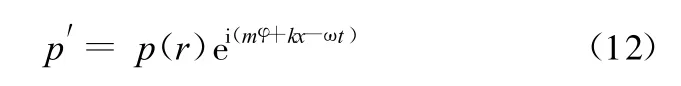
式中,p(r)为实数;m为周向模数(为整数);k为轴向波数;ω为角速度。

而对于其他流体变量,也可以作相似的假设。将式(12)代入式(10)可得

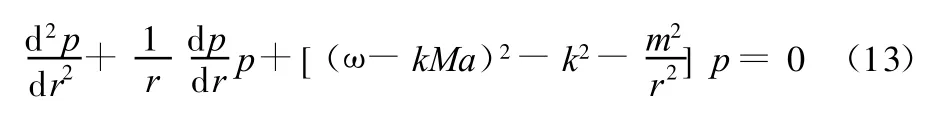
式(13)是一个典型的贝塞尔方程,其通解为

式中,A、B为常数;Jm、Ym分别为m阶的第一类和第二类贝塞尔函数;下标n为径向模数。

从式(13)可以看出,如果βmr为其解,那么-βmn也是其解,因此可以只考虑非负的βmn。从而在式(14)中,m和βmn有以下几种组合方式：

(1)m=βmn=0。由于第二类贝塞尔函数在0处趋于-∞,为了保证解有界必有B=0,此时解退化为一个常数,也就是p=A,这个解就是平面波。

(2)m ＞0且βmn=0。此时p为零,我们只关注非零解,所以可以排除此类情况。

(3)m ≥0且βmn＞0。此时根据边界条件式(11)可得

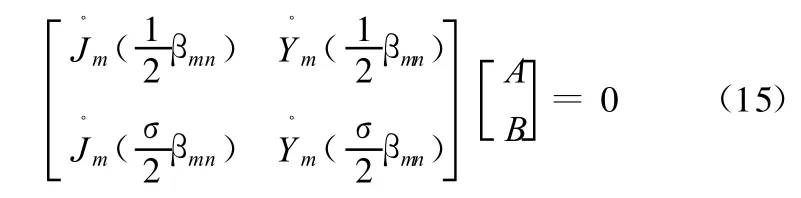
式(15)中,为了使A和B有解,必须让左边矩阵的行列式等于零,即

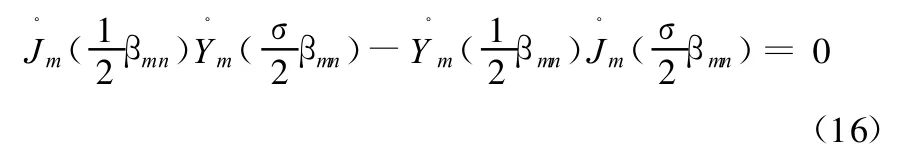
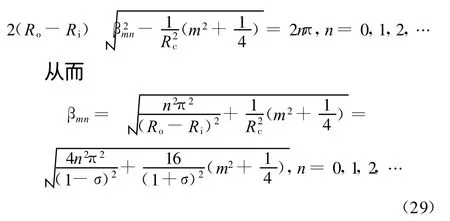
式(16)就是圆环管道内声波的色散关系式,求βmn的根的方法将在下一节讨论。找出了 βmn的值,也就确立了波数k和角速度ω的关系。将β2mn=(ω-kMa)2-k2改写为

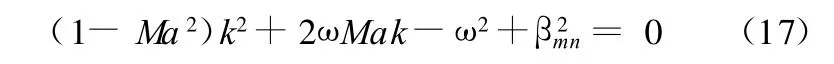
从而

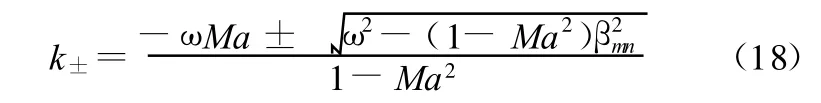
式中,k+、k-分别为声波向下(游)和上(游)传播。

声波在传播过程中应该既不被衰减也不被放大,因此 k必须为实数,并且必须有ω2≥(1-Ma2)β2mn。ω2=(1-Ma2)β2mn对应的频率称为截止频率,ω2＞(1-Ma2)β2mn对应的声模态称为传播声模态,ω2＜(1-Ma2)β2mn对应的声模态称为截止声模态。

在式(18)中,声波的角速度ω一般为已知数,也可以通过声波的频率求得,即 ω=2πf。但需要注意的是,由于这里所有物理量都是量纲一单位,频率也应该为量纲一单位。频率为 f 0(Hz)的声波对应的量纲一频率为

通过式(16)求得βmn,ω也已知,则可通过式(18)求得波数k,从而式(14)中声压的解变为

式中,Amn为声压幅值,由声功率决定。

将式(20)代入式(12)可得

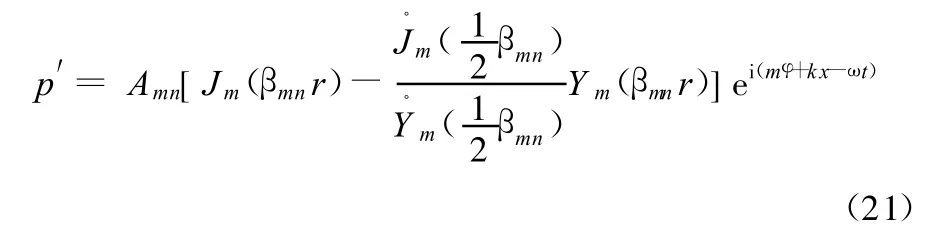
将式(21)代入式(7)中,可以得到声波各个变量的表达式：

2 求解βmn的方法

为了求解圆环管道中的声模态,必须首先通过式(16)才能得到βmm。然而,此方程为超越方程,不可能得到简单的解析解,所以需要利用数值解法,如牛顿迭代法求解。在利用牛顿迭代法求解的过程中,需要给定初值。为了得到这些初值,可用薄管近似方法。假定非常小,然后用R c代替式(13)中的r,可得

令 p=eλr,则式(23)变为

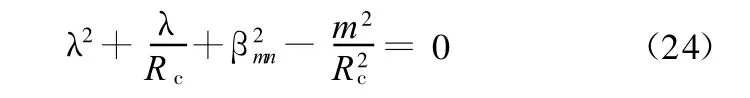
从而

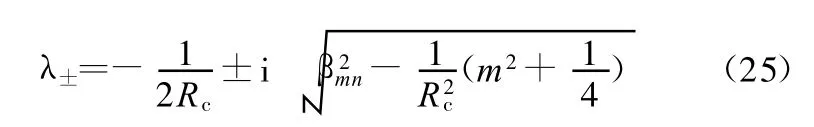
式(23)的解为

将边界条件式(11)代入式(26),可得

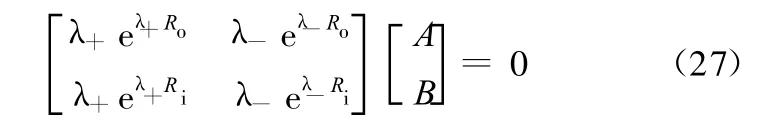
为了得到非零解,式(27)中系数矩阵的行列式必须为零,即

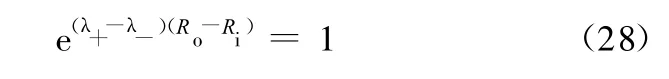
将式(25)代入式(28)可得

当管道内外径之比σ比较大的时候,这种薄管近似给出的初始值比较精确。然而当σ比较小的时候,圆环管道和薄管有很大的差异,如果用式(29)估计初值,则会产生根的排列混乱和丢根的情况。此时可以采用多次薄管近似逐渐逼近的方法或者二分法来估计初值。设函数

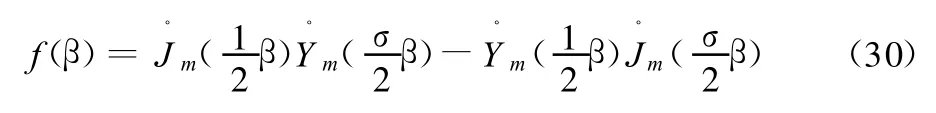
则式 (16)的根就是由式(30)确定的函数f(β)的零点。m=22且σ=0.4时,f随β变化的曲线如图2所示。根据函数图像的形状,完全可以用二分法求根的初值或者直接求根。

图2 m=22且σ=0.4时 f(β)的函数曲线图

3 管道中的声功率

式(22)中与声学变量幅值相关的常数Amn由声功率决定。如果声功率为P,则声功率级定义为

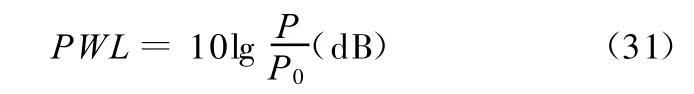
其中P0为基准声功率,P0=10-12W。令P为量纲一单位的声功率,则

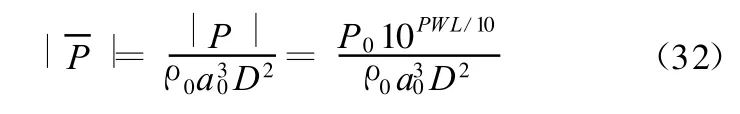
另一方面,平均流的声强为[9]

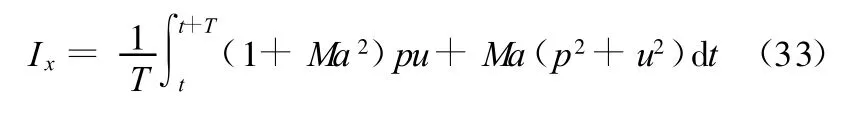
式中,p、u分别为声扰动的压力和速度的实部。

对单个的声模态有

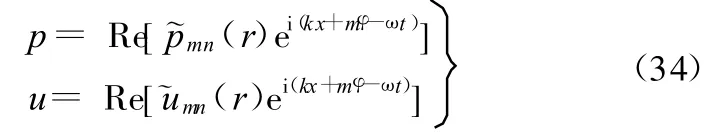
所以管道中的声功率为

不难证明,当T→∞时,对于任意复数C和G有

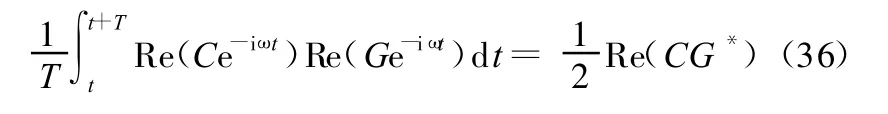
式中,G*为G的共轭。

因此

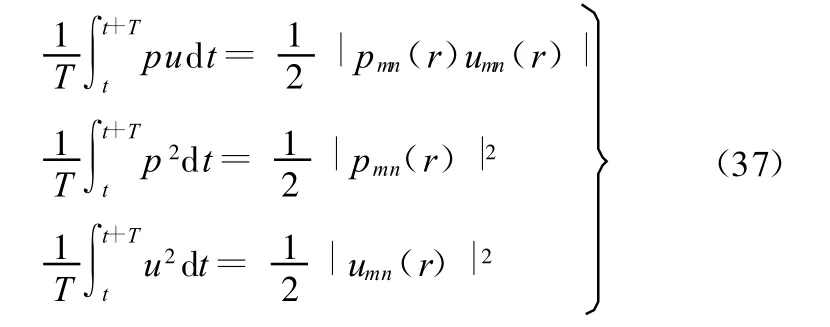
将式(37)和式(35)代入式(33)可得单个声模态的声功率：

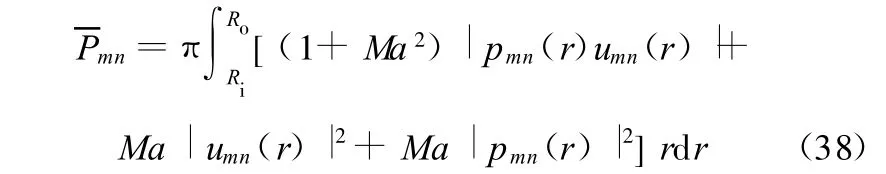
将式(22)代入式(38),可得

至此,如果给定单个声模态的声功率、频率、周向模态m以及平均流的马赫数Ma,则可以完全确定圆环管道中声波各个变量的解析表达式。

4 算例

下面利用有平均流的圆管声模态来模拟涡扇发动机进气道的噪声传播过程。某发动机进气道的结构如图3所示,其中 x代表进气道的轴向,r代表进气道的半径方向(计算将在柱坐标中进行)。发动机工作时风扇将气体由进气道吸入到内外涵道。风扇产生的噪声是发动机的一个主要噪声源,这些噪声可以沿着气流或者逆着气流传播。这里仅研究风扇噪声逆着气流在进气道传播的过程。为了便于计算,作如下简化：①整个进气道关于x轴对称;②将圆环管道中单个声模态作为输入的风扇噪声。从图3可以看出,这个进气管道在

图3 涡扇发动机进气道结构图

风扇面附近近似为一个圆环形的管道,因此可以认为,风扇产生的噪声是由无数个圆环管道声模态叠加而成的。假定其中的单个声模态在周向解析(m已知,为输入参数),从而所有的声学量都可以写成如下形式：

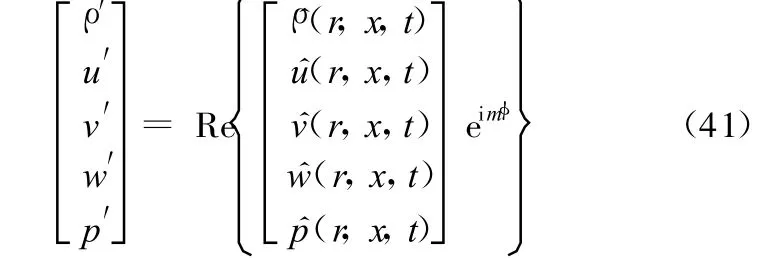
其中带有上尖括号的量均为复数。

在以上简化下,控制方程变为

从而将一个三维问题转化为二维问题。计算中先利用保形映射方法将物理空间(x-r)中转子和机匣的壁面曲线映射到计算空间(ζ-η)中的两条相互平行的直线上,如图4所示。由于进气道满足轴对称条件,所有计算只需要在第二象限进行,所以图4中仅显示转子和机匣在第二象限中的像。映射后转子和机匣的像之间的距离为h。计算时首先在计算平面中设计网格,然后再将网格逆变换到物理空间中。考虑到计算需求和效率,计算区域在计算平面中的大小选为6h×4h,这个区域对应在物理坐标中的范围如图5所示。

图4 转子和机匣壁面曲线在计算空间中的像

图5 物理空间中的计算区域图

计算中时间和空间离散采用多网格尺度 -多时间步色散关系保持(DRP)方法[10]进行。计算中采用如下边界条件：①A-B-C-D边界采用辐射边界条件[11],使声波能无反射地穿过计算区间;②A-K采用轴对称边界;③机匣和转子壁面上采用滑移边界条件,利用外伸点(ghost point)法[12]实施;④风扇表面(E-H)采用理想匹配层(PML)边界[13]输入声波并吸收反射声波,保持数值稳定。

作为模拟算例,这里仅计算输入频率为1614Hz,声功率级为120dB,周向模数m=22时n=1和n=4两种情况。在计算声场之前,先计算平均流场,使得风扇表面的马赫数为0.3。计算后的瞬时声压云图如图6和图7所示,可以看出,风扇面输入的不同声模态在进气道以及进气道附近的区域传播过程差别较大,这也正是众多学者研究进气道噪声传播机理的原因。

5 结论

(1)声波在平均流中的传播的控制方程为线性欧拉方程,在均匀流的圆环管道中,平均流只沿着轴向方向流动,从而可以使方程大大简化。

(2)传播中的声波可以看成是多个Fourier模态的组合。对于圆环管道中的单个Fourier模态,其轴向波数k、周向模数m、角速度ω以及平均流的马赫数Ma等必须满足色散关系式。

(3)在其他条件给定时,圆环管道中的声波存在一个截止频率,大于截止频率的声模态可以在管中传播,而小于截止频率的声模态则不能在管中传播。

(4)给定了声功率级,平均流的马赫数,入射声波的频率、旋转模数、径向模数和管的几何尺寸以后,便唯一确定了单个Fourier模态的声波的解析表达式。

(5)可利用圆环管道的声模态作为风扇产生的噪声来研究涡扇发动机进气到噪声传播规律,非均匀流场对不同声波模态的散射效果不同。

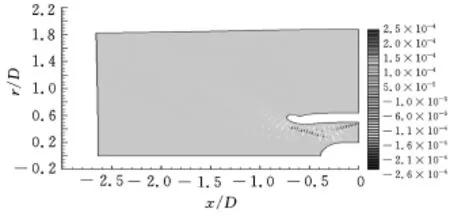
图6 输入声波m=22,n=1,PWL=120d B时的瞬时声压图

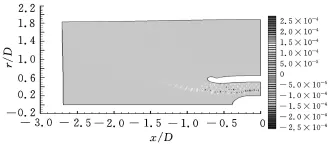
图7 输入声波m=22,n=4,PWL=120d B时的瞬时声压图

[1] Dahl M D,Envia D,Huff D,et al.Fourth Computational Aeroacoustics(CAA)Workshop on Benchmark Problems[C]//Brook Park,Ohio：NASA Conference Publication,2004：212954.

[2] Rienstra S W.A Classification of Duct M odes Based on Surface Waves[J].Wave Motion,2003,37(2)：119-135.

[3] Ayub M,Tiwana M H,Mann A B.Propagation of Sound in a Duct with Mean Flow[J].Communications in Nonlinear Science and Numerical Simulation,2009,14(9/10)：3578-3590.

[4] Tam C K W,Ju H,Chien EW.Scattering of Acoustic Duct Modes by Axial Liner Splices[J].Journal of Sound and Vibration,2008,310(4/5)：1014-1035.

[5] Gabard G,Astley R J.A Computational Modematching Approach for Sound Propagation in Three-dimensional Ducts with f low[J].Journal of Sound and Vibration,2008,315(4/5)：1103-1124.

[6] Yang B,Wang T Q.Investigation of the Influenceof Liner Hard-splices on Duct Radiation/Propagation and Mode Scattering[J].Journal of Sound and Vibration,2008,315(4/5)：1016-1034.

[7] McAlpine A,Astley R J,Hii V J T,et al.Acoustic Scattering by an Axially-segmented Turbofan Inlet Duct Liner at Supersonic Fan Speeds[J].Journal of Sound and Vibration,2006,294(4)：780-806.

[8] Brun C,Goossens T.3D Coherent Vortices in the Turbulent Near Wake of a Square Cylinder[J].Comptes Rendus Mcanique,2008,336(4)：363-369.[9] Atassi O V.Computing the Sound Power in Nonuniform Flow[J].Journal of Sound and Vibration,2003,266(1)：75-92.

[10] Tam C K W,Kurbatskii K A.Multi-size-mesh Multi-time-step Dispersion-relation-preserving Scheme for Multiple-scales Aeroacoustics Problems[J].International Journal of Computational Fluid Dynamics,2003,17：119-132.

[11] Tam C K W,Webb JC.Dispersion-relation-preserving Finite Difference Schemes for Computational Acoustics[J].Journal of Computational Physics,1993,107(2)：262-281.

[12] Tam C K W,Dong Z.Wall Boundary Conditions for High-order Finite-difference Schemes in Computational Aeroacoustics[J].Theoretical and Computational Fluid Dynamics,1994,6(5/6)：303-322.

[13] Hu F Q.Development of PML Absorbing Boundary Conditions for Computational Aeroacoustics：A Progress Review[J].Computers and Fluids,2008,37(4)：336-348.