子阵级相控阵差波束旁瓣抑制新方法

邱朝阳 雷丽丽 胡 航 董 晔

(1.中航雷达与电子设备研究院航空电子系统射频综合仿真航空科技重点实验室， 江苏 无锡 214063；2.哈尔滨工业大学电子与信息工程学院，黑龙江 哈尔滨 150001)

1. 引 言

在相控阵雷达特别是多功能相控阵雷达中，阵列常常包含数千个阵元，因而,通常采用子阵结构[1-2]，只能得到子阵的数字化输出。此时需要采用子阵级阵列处理技术。如相控阵雷达应用自适应数字波束形成(Adaptive Digital Beamforming，即ADBF)时，需要采用子阵级ADBF；此时阵元级模拟加权用于抑制静态方向图的旁瓣，而子阵级数字加权用于进行自适应[3]。

很多相控阵雷达采用单脉冲技术测角，此时必须同时形成和、差波束，并对和、差波束的旁瓣进行抑制。若在阵元上采用两种形式的模拟加权，即和波束的Taylor加权及差波束的Bayliss加权[4]，则对包含成千上万阵元的阵列来说，需要高昂的成本。

根据子阵级相控阵的结构及组成特点，可在阵元级只用Taylor加权抑制和波束的旁瓣，而抑制差波束旁瓣的任务由子阵级数字加权完成[5]。由于用数字加权取代了模拟(Bayliss)加权，从而大大降低了硬件成本与复杂度，并充分利用了数字处理的灵活性。

提出利用遗传算法优化子阵级加权，以得到良好的旁瓣抑制效果。遗传算法是模拟生物遗传和进化过程的优化概率搜索算法，能够在搜索过程中自动获取和积累有关的搜索空间信息，并自适应地控制搜索过程以求得最优解。它提供了求解复杂优化问题的通用框架，可得到全局最优解，且不受求解问题的约束，有很强的鲁棒性；尤其适用于传统优化方法解决不了的复杂非线性问题[6]。

为用遗传算法优化子阵级加权，构造了两种适应度函数：加权向量和方向图参数。为提高旁瓣抑制性能并改善优化效率，对常规的只使用一种适应度函数的遗传方法进行了改进，提出将优化过程分为两个阶段，且分别使用加权向量和方向图参数作为适应度函数。

仿真结果表明，与常规遗传方法相比，本文的改进遗传方法不仅大大提高了优化效率，且得到了更好的旁瓣抑制效果。

2. 基于改进遗传算法的子阵级加权的优化

2.1 阵列模型

设由M个全向阵元组成的平面阵位于xoy平面上，其中第1个阵元位于坐标原点为参考阵元，第m(m=1，…，M)个阵元的坐标为(xm，ym)。用(θ，φ)表示俯仰角和方位角，设阵列波束指向为(θ0，φ0)；阵元采用Taylor加权，且设第m个阵元的权值为wm；波束指向由移相器控制。设阵列被划分为L个子阵，其子阵转换矩阵T为M×L维矩阵，它是描述子阵级相控阵的主要参数，决定了其组成与结构。子阵转换矩阵由阵元数、阵元分布、子阵数、子阵结构、阵元级加权及移相等共同决定:

T=Φ0WT0

(1)

式中：W=diag(wm)m=1，2，…，M；Φ0=diag[φm(θ0，φ0)]m=1，…，M，其中φm(θ，φ)=exp{-j2π[xmsinθcosφ+ymsinθsinφ]/λ}；T0为M×L维子阵形成矩阵：在其第l(1≤l≤L)列的所有元素中，只有与第l个子阵的阵元序号相对应的元素值为1，其余均为0(非重叠子阵情况下，T0的列向量相互正交)[7]。

在波束指向处的子阵级导向向量为

asub(θ0，φ0)=THa(θ0，φ0)

(2)

式中

a(θ0，φ0)= [φ1(θ0，φ0)，…，φm(θ0，φ0)，…，

φM(θ0，φ0)]T

令u=sinθcosφ、v=sinθsinφ分别表示(θ，φ)方向的单位向量在x和y方向的投影，用wsub_Δ表示用于抑制差波束旁瓣的L维子阵级权向量，则子阵级差波束的方向性函数为

fΔ(u，v)= (wsub_Δ)H[asub(u，v)∘

asub(-u0，-v0)]

(3)

式中,“∘”表示Hadamard积。

2.2 基于遗传算法的子阵级加权的优化

为抑制差波束旁瓣，常规考虑是在阵元上采用Bayliss加权。然而，根据相控阵的结构及特点，可采用子阵级数字加权。

遗传算法是一种高效的优化技术，广泛应用于阵列处理[8-11]。利用遗传算法优化子阵级加权。为此需要解决两个问题：一是优化目标的编解码方法，二是适应度函数的选择。

2.2.1 编码方法

采用实数编码方案。与二进制编码相比，其可快速收敛并避免优化过程陷入局部最优解。它避免了将二进制转换为十进制的运算，降低了运算代价；且具有较好的收敛性能。

设种群大小即染色体个数为Msub，它由阵元数和子阵数决定。种群中每个染色体对应一个子阵级权向量，用xsub_j表示其第j(j=1，2，…，Msub)个染色体；用xsub_j_l表示第j个染色体中的第l个基因，它是第l个子阵的权值；则

xsub_j={xsub_j_1，…，xsub_j_l，…，xsub_j_L}

(4)

2.2.2 适应度函数

在用遗传算法优化子阵级加权的过程中，适应度函数的选取对旁瓣抑制效果有很大影响；其选择不当可能影响全局优化性能，甚至收敛于局部最优解。

基于不同优化目的，构造以下两种适应度函数。

1)使子阵级加权等效的阵元级加权在最小均方误差意义下逼近Bayliss加权。

此时将适应度函数表示为fweight，则

(5)

式中,‖‖2表示2范数。

2)使子阵级加权得到的方向图的旁瓣电平尽可能低

将子阵级加权得到的方向图的旁瓣电平作为适应度函数，从物理意义上更为直观。但是，此时适应度函数中不应只考虑旁瓣电平，还要在特定方向形成差波束的凹口且保证足够的零深；同时要使波束展宽限制在一定范围内。

因而，描述差波束方向图特性的参数应包括旁瓣电平、主瓣宽度及凹口零深3个参数。将所期望的旁瓣电平、波束宽度和零深分别用SLLdes、BWdes和NDdes表示，将用遗传算法优化后的旁瓣电平、波束宽度和零深分别用SLL、BW和ND表示；且令

ΔSLL=SLL-SLLdes

ΔBW=BW-BWdes

ΔND=ND-NDdes

(6)

从而，基于方向图参数的适应度函数fpatt为

fpatt=KSLL(ΔSLL)2+KBW(ΔBW)2+KND(ΔND)2

(7)

式中，KSLL、KBW及KND为权重。

2.2.3 优化过程

为用遗传算法对子阵级加权进行优化，可选择fweight或fpatt作为适应度函数。其实现过程是：首先对子阵级加权进行编码，产生初始种群并根据适应度函数计算初始的适应度值，然后进行选择、交叉及变异，再计算适应度值，判断适应度值或遗传代数是否满足条件；若是则进行解码并退出优化过程，否则重复上述过程，直到满足条件为止。

2.3 基于分阶段、多适应度函数的改进遗传算法的子阵级加权优化

对于目前的各种遗传算法，在每个独立的优化空间内均只使用一种适应度函数。如上述的子阵级加权的优化过程中，适应度函数可选择fweight或fpatt。本文称其为常规的基于遗传算法的子阵级加权优化方法，简称常规方法。

常规方法中，选择不同适应度函数时优化效果不同。采用fweight的特点是：1)运算效率高，收敛速度快。这是因为遗传算法的运算时间在很大程度上受适应度函数复杂度的影响，而fweight具有较为简单的形式。2)旁瓣抑制效果不理想，其原因是此时优化对象只是加权向量。

而采用fpatt作为适应度函数的特点是：1)直接对旁瓣电平进行优化，旁瓣抑制效果明显优于fweight；2)适应度函数中包含多种参数，相当于增加了约束条件(零深)，从而导致算法稳定性较差且容易陷入局部最优解；同时运算效率低，收敛缓慢。因而，对常规方法不论采用哪种适应度函数，都具有较大的局限。

为此，对常规方法进行改进，提出将优化过程分为2个阶段，且每个阶段分别采用不同的适应度函数，并称其为改进方法。其中第1阶段用于对旁瓣电平进行初步优化，第2阶段在第1阶段的基础上，进一步改善旁瓣抑制效果。

改进方法中，要求两个适应度函数既相互独立又相互关联。其中相互独立是指二者彼此不受影响和制约；而相互关联是指二者具有相关性，即第1个适应度函数的优化能够为后续的第2个适应度函数的优化缩小搜索范围，以使其能够更快收敛。

改进方法的实现过程为：第1阶段使用fweight作为适应度函数进行遗传优化，得到最优解后，停止本阶段运算。第2阶段中，先将第1阶段的优化结果按适应度值由大到小进行排列，并选择一定比例的优良子代组成新种群；然后以fpatt作为适应度函数进行优化，当达到一定代数后退出遗传过程。

选择fweight作为第1阶段的适应度函数的原因是其实现简单，可有效提高运算效率。因而第1阶段完成后，可大大减小第2阶段fpatt作为适应度函数的最优解的搜索范围，使其仅用很少的遗传代数就可得到较好的优化效果，且避免陷入局部最优解。

图1给出了利用改进遗传方法进行子阵级加权优化的流程图。其中，在完成第1阶段优化过程后，

需要进行适应度函数的转换并重新计算新的初始适应度值，再进入第2阶段。

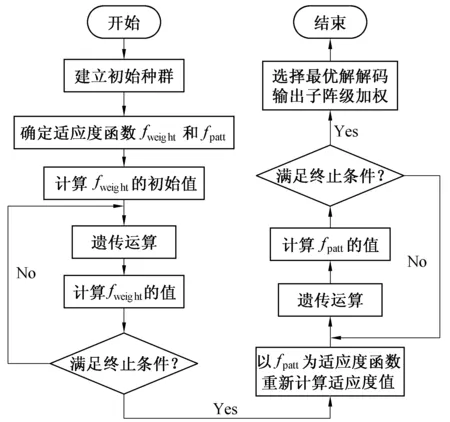
图1 基于改进遗传算法的子阵级加权的优化流程

3. 仿真结果

3.1 仿真参数

设平面阵包含30×30个全向阵元，放置在xoy平面的矩形网格上，x和y方向的阵元间距均为d=λ/2。阵元在x和y方向均采用-40 dB Taylor加权，波束指向为(0°，0°)。阵列被划分为10×10个非重叠子阵，且各子阵均为矩形阵。

子阵级加权用于逼近-30 dB Bayliss加权。在常规遗传算法中，初始种群大小设为100，遗传代数取为1300；采用10进制编码，且取值范围为[-5，5]。

期望的差波束旁瓣电平设为-30 dB，高于和波束的旁瓣(-40 dB)，其原因是差波束用于目标跟踪，即使具有较高的旁瓣也不会导致由杂波等引起的虚警；而且旁瓣过低将导致差波束其它性能的下降(如主瓣展宽及零深减小)。

3.2 优化结果

图2(看202页)给出了由常规遗传算法及改进遗传方法得到的差波束方向图；为便于比较，图中同时给出了不采用子阵级加权时的方向图。图中，各方向图的旁瓣电平如表1所示。由图2可见，与不采用子阵级加权相比，常规方法可对旁瓣进行一定抑制：由表1可见，其旁瓣抑制了6.92 dB。由图2可见，改进方法与常规方法相比，旁瓣抑制效果得到较大改善，同时保持了主瓣宽度。由表1可见，改进方法与常规方法相比，旁瓣改善了3.44 dB。

表1 不同方法得到的旁瓣电平/dB

3.3 收敛性能

图3给出两种遗传方法的优化曲线，即适应度函数值随遗传代数的变化关系。其中图3(a)是常规方法中，在1300代的遗传过程中fweight解的变化曲线；图3(b)是改进方法的第2阶段中，在20代遗传过程中fpatt解的变化曲线。由图可见，不论是fweight还是fpatt作为适应度函数，优化过程均收敛，表明这两种遗传优化方法均有效。

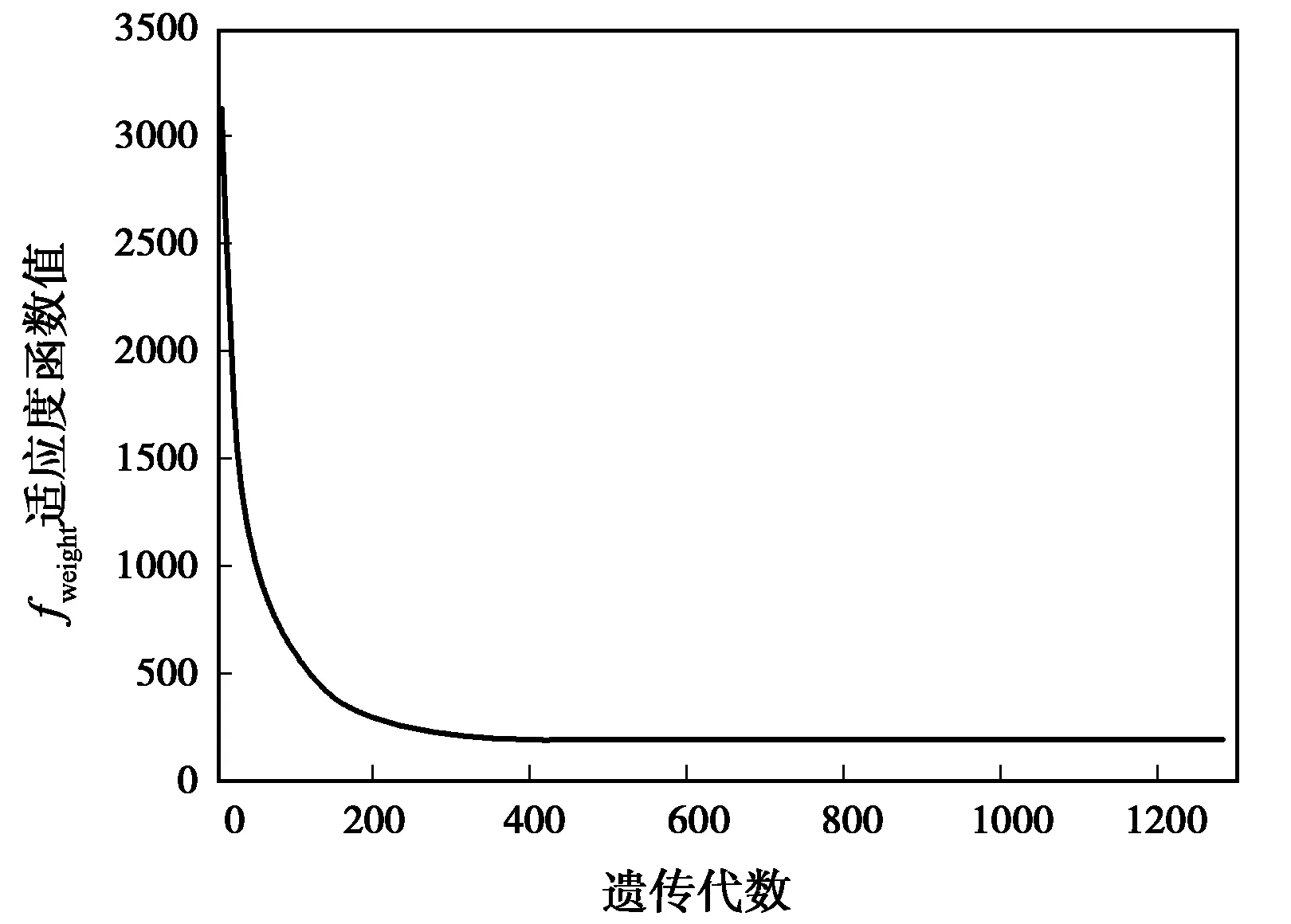
(a)常规fweight解

(b)改进方法：fpatt图3 两种方法的遗传优化曲线

与常规方法相比，改进方法大大节省了运算时间：在第1阶段中，1300代遗传运算的耗时只有195.7 s；而在相同条件下，第2阶段中每1代遗传运算的耗时就约为150 s；即第1阶段的全部运行时间与第2阶段中每1代的运算时间基本相当。对于改进方法，由于预先进行了第1阶段的优化，因而大大减少了第2阶段的遗传代数，使其至少节省了200代运算，从而大大提高了优化效率。

4.结 论

1)利用遗传算法得到的子阵级加权可有效抑制相控阵的差波束旁瓣。

2)本文提出的将优化过程分为两个阶段、且分别使用加权向量及方向图参数作为适应度函数的方法较好地解决了优化过程的稳定性问题，提高了优化效率，且改善了旁瓣抑制效果。

3)分阶段、多适应度函数的处理思想可推广到其它遗传优化问题中。

[1] NICKEL U. Subarray configurations for digital beamforming with low sidelobes and adaptive interference suppression[C]//Proc. IEEE International Radar Conference. USA, 1995: 714-719.

[2] LOMBARDO P, CARDINALI R, PASTINA D, et al. Array optimization and adaptive processing for sub-array based thinned arrays[C]//Proc. International Conference on Radar. Adelaide Australia, 2008: 197-202.

[3] BURGER W, NICKEL U. Space-time adaptive detection for airborne multifunction radar[C]// Proc. IEEE International Radar Conference. Rome Italy, 2008: 635-640.

[4] SKOLNIK M I. Radar handbook[M]. 2nd ed. New York: McGraw-Hill, 1990.

[6] 周 明, 孙树栋. 遗传算法原理及应用[M]. 北京: 国防工业出版社, 2002.

[7] 胡 航, 刘伟会. 一种有效的子阵级波束扫描旁瓣抑制方法[J].电波科学学报, 2009, 24(4): 593-597.

HU Hang, LIU Weihui. A kind of effective side lobe suppression approach for beam scanning at sub-array level[J]. Chinese Journal of radio science, 2009, 24(4): 593-597. (in Chinese)

[8] HAUPT R L. Phase-only adaptive nulling with a genetic algorithm[J]. IEEE Trans. on AP, 1997, 45(7): 1009-1015.

[9] JONES E A, JOINES W T. Genetic design of linear antenna array[J]. IEEE Antennas and Propagation Magazine, 2000, 42(3): 1009-1015.

[10] WEILE D S. The control of adaptive antenna array with genetic algorithms using dominance and diploidy[J]. IEEE Trans. on AP, 2001, 49(10): 1424-1433.

[11] YEO B K, LU Y. Array failure correction with a genetic algorithm[J]. IEEE Trans. on AP, 1999, 47(5): 823-828.