时域有限差分法分析混响室中场的均匀性

黄 华 牛中奇 白 冰

(西安电子科技大学电子工程学院,陕西 西安710071)

1.引 言

从众多研究者的工作可知,混响室可采用多种数值方法进行仿真分析：矩量法(MOM)[1];时域有限差分法(FDTD)[2-6];有限元法(FEM)[7-8];FDTD与MOM混合法[9];FEM与FDTD混合法[10];平面波积分表示法[11];传输线矩阵法(TLM)[12]等。在经典的仿真分析中,建立的混响室模型一般由混响室的内部空间、搅拌器及天线三部分组成[13]。图1所示即为混响室测试示意图。

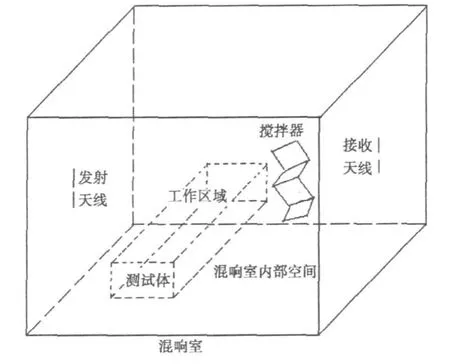
图1 混响室测试示意图

通常,仿真计算中耗费的时间与混响室的体积、六个壁面所用导体的电导率、电磁波的频率范围以及受试设备自身的特性有关,然而这会使得计算量很大,因而十分耗时,有时要用微机实现仿真几乎是不可能的。为克服这一困难,Franco Moglie把重叠平面波理论[14]用到了该问题的处理之中,其基本思路是,用重叠平面电磁波替代经典仿真分析中当搅拌器转动时产生的向不同方向传播的电磁波,用在计算程序中设置的对源于不同方位的重叠波的重复计算次数等效经典仿真分析方法中的搅拌器的离散步进次数,而在相应的模型中只保留受试对象,如图2所示。这样便可模拟混响室内真实的电磁环境。然而,在该文献中并没有分析重叠入射波数目与混响室内场分布之间的相互关系,基于此,本文将对该问题进行研究,寻求其中的规律性以便为工程实践提供理论指导。

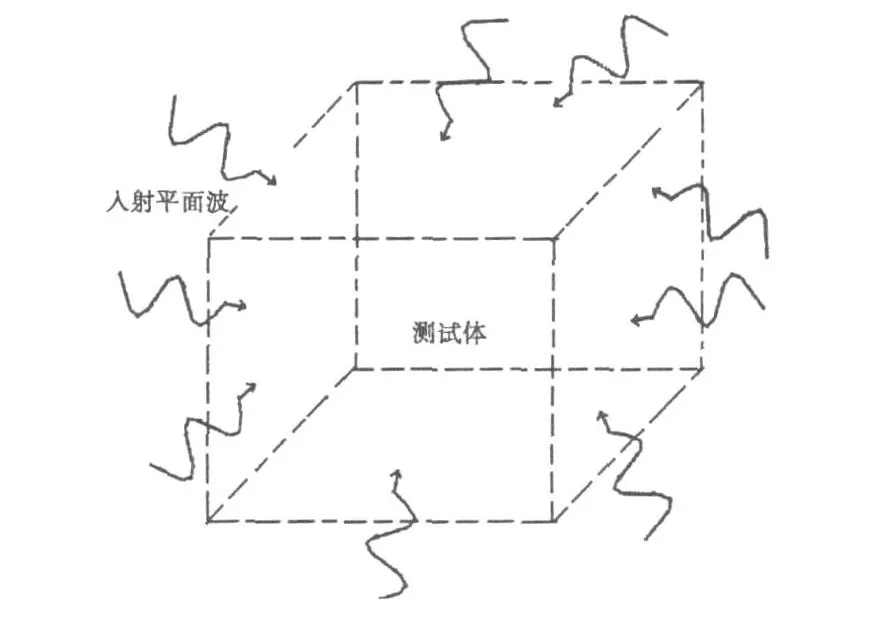
图2 随机重叠入射平面波

2.方法简介

2.1 随机平面电磁波的生成

要把重叠平面波理论用于混响室内场的仿真分析,解决的关键问题是重叠平面波的生成。注意到搅拌器转动时所产生的电磁波的传播方向是随机变化的这一特征,本文用所处方位是随机的一组等效源产生的所谓随机平面电磁波对其进行模拟。又由于本文将采用FDTD法对混响室内的场进行仿真计算,而在FDTD法中,入射波源是设置在总场区与散射场区的分界面即所谓的连接边界面上的,因而,上述的一组等效源设置的具体位置应在连接边界上。同时,构成这一组源的各个子等效源的位置参数及各个子等效源辐射的电磁参数在FDTD程序中应被设定,在每一暂态的迭代过程中只需调用即可。这些参数包括,每个子等效源在球坐标系中的坐标r、θ和φ以及由它们辐射出的电磁波的极化角α,即平面波的电场矢量与x轴的夹角,如图3所示。图中P点为一个子等效源所在点,E、H和n分别为由该等效源所产生的电磁波的电场、磁场和传播方向的单位矢。为了模拟搅拌器转动时所产生的电磁波的随机性,设置在球坐标系中的一组等效源的分布方位亦应是随机的,也就是说,一系列子波源设置点的方位角θ和φ是随机的。但值得注意的是,θ和φ的随机性要受到球坐标中坐标变量取值范围的约束,同时在对θ和φ的随机取值中还要防止等效源在某一区域内的分布过于集中,以致带来对混响室内场随机分布模拟的失实,因而,也要设置约束条件来予以防止,鉴于以上考虑,设置以下约束条件：

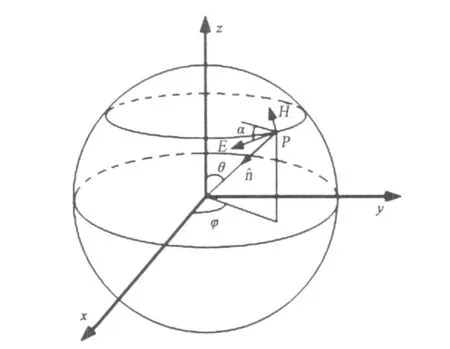
图3 等效源的方位及其产生的电磁波的参数

1)θ的随机取值应在[0,π]之间,以便满足所用坐标系的约定。在此前提下,具体的随机取值过程是,在 Fortran中首先由 random_element()在[0,1]之间抽取随机数,然后再乘以π弧度即可得到一系列θ的随机值。

2)φ的随机取值应在[0,2π]之间,以满足所用坐标系的约定。对φ的随机取值中应特别值得注意的问题是,有时随机取值的结果有可能出现某一区域的取值样本过于密集,这种情况最有可能发生在高纬度即θ很小或θ很大的区域,对于发生这种情况的原因可作这样的解释：当θ很小或θ很大时,同球面上与之对应的纬度圈的周长2πrsinθ将很小,因而在取同样数量的φ样本个数的情况下,其样本点的密度便远大于其它纬度圈上的密度,因而若不加约束地按此种情况随机设置等效源来模拟混响室内的场分布,其结果将严重失实。为此,给予φ的随机取值附加了这样的约束：令φ=ψ/(2×sinθ),对 ψ随机取值,当ψ的某一随机值使得与之相应的φ值落在[0,2π]之内,则保留之,否则则弃之重取,直至所取φ的个数满足预设的等效源的个数为止。

3)α是线极化波的极化方向的表述,定义是电场矢量与x轴的夹角,称其为极化角,其值在[0,2π]范围内。设各等效源产生的电磁波的电场幅度均是1,即Em=1 V/m.

上述约束条件中,θ和ψ是两个相互独立的随机取样变量,其中约束条件2)是为了使所选取的一系列等效源分布点P不至于过分密地集中在球面的两极附近,以便保证之后采用FDTD法时,设置在六个连接边界面上的波源分布是较为均匀的,这样才可较好地模拟在搅拌器转动时所产生的电磁波的传播方向是随机的效果。

2.2 随机平面电磁波的引入

在仿真分析中,一是要对电磁波的特性进行设置以模拟实际空间中实际存在的电磁波的特征,二是要把电磁波引入到仿真分析区域内的各点,以模拟电磁波在实际空间内的传播。一般说来对电磁波进行设置的方法有两种：一是解析方法,二是一维FDTD方法[15]。由于由一维FDTD方法引入的入射波在总场区内的分布较为均匀且在散射场区泄漏较小,故本文选用第二种方法。在下面的仿真分析中,由程序设置的是连续的正弦平面电磁波,为了使引入到各点的正弦波能够快速地达到稳定,在开始的前半个周期加入了一个升余弦开关函数,而在后半个周期仍为正弦函数,如式(1)所示,其中,Em为电场振幅,f为电磁波的频率,T为波的周期。

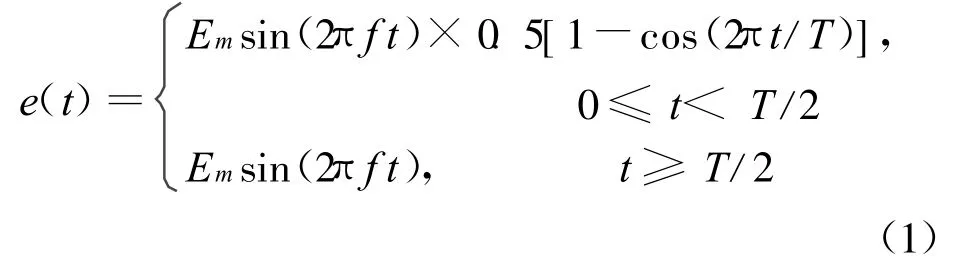
将Maxwell方程组中两个旋度方程差分离散,再用一维FDTD法可得由电场表述磁场的如下表达式。

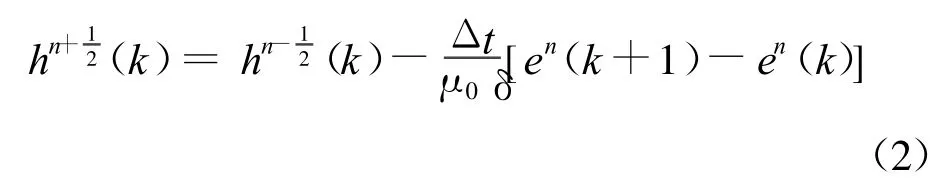
式中：μ0为真空中的磁导率;δ为讨论空间的网格步长;Δt为计算中的时间步长;n为计算迭代的时间步数;k为空间网格的位置。

2.3 程序实现

本文用Fortran语言进行计算编程。下面对主要步骤予以简介。

2.3.1 电磁波的引入

如2.2节所述,电磁波是采用一维FDTD法引入的,且对电磁波的种类及其表达式作了说明。现在介绍如何用Fortran程序予以实现。首先,在连续的正弦波上等间隔地采样10000个,然后把这10000个样本数据由一维FDTD法逐次推进到讨论空间的每个网格内,每一时刻各网格内均占有10个采样数据。这样设置好后,再将由各个角度入射的波的传播方向投影到直角坐标系的x、y、z方向上。当把如式(1)所示的、其参数Em、f和T为固定取值的、来至P1点等效源所产生的电磁波在混响室内的场分布计算完以后,再对入射波参数进行更新,即对P2点的等效源产生的电磁波在混响室内的场分布进行计算,直至把Pn点的等效源产生的场计算完毕。之后对场进行矢量叠加可得总场。

2.3.2 归一化设置

由于同一电磁波的电场与磁场的振幅的数值之比为波阻抗,而对于空气而言波阻抗η=377Ω,这表明,电场与磁场的量值不在同一数量级,为了在计算中获得同样的准确度,需对这两个量进行归一化处理[16],而当计算程序结束进行数据存储时再将其还原。本文是对电场进行归一化处理的,即程序处理时,令˜E=E/η而H不变。另外,计算时,取讨论空间中沿各坐标方向的步长相等,即Δx=Δy=Δz=δ,并令讨论空间内的电导率σ=0,这样Maxwell方程离散式前的系数就只剩下了 Δt/(ε0δ)和Δt/(μ0δ)两项。由于

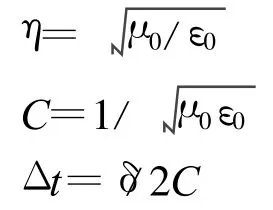
故有

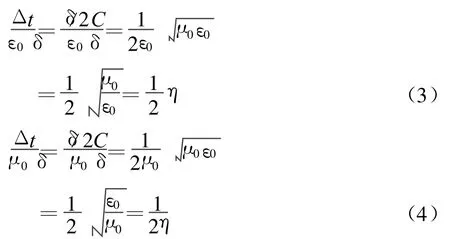
将式(4)代入式(2),有

若将上式中的因子[en(k+1)-en(k)]/η记为(即归一化为),则式(5)可写为

将其它的离散式进行同样的处理。再将归一化电场˜E=E/η代入式(1),有

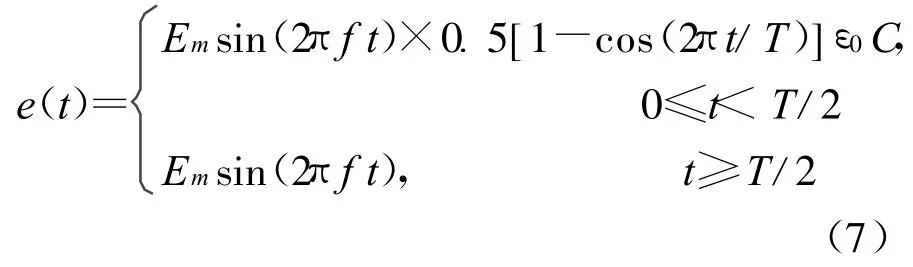
上面是对电场归一化处理的具体步骤,存储数据时再用E=η˜E对电场进行还原。当然,在方法上也可将磁场归一化为˜H=ηH而E不变,处理后可得与上述类似的表达式,只是在数据存储时需对磁场进行还原。

3.仿真计算及结果分析

作为有实际背景的事例,计算中将讨论空间的网格数取为90×90×90,其中沿各坐标方向,连接边界与吸收边界的距离为10个网格。取电磁波频率为915 MHz;空间步长为0.025 m;时间步长为Δt=4.5×10-11s,Δt这样的取值是为了满足数值稳定性的要求。对计算数据的最终处理是将由Fortran程序计算出的数据导入Matlab程序中完成的。

3.1 对平面电磁波正弦特征的检验

2.2节中已经说过,在本文中由程序设置连续平面正弦电磁波以对在正弦电磁波随机入射时混响室内的场分布进行仿真,但为了使推进到各网格的正弦波快速地达到稳定状态以满足仿真要求的条件,因而作了式(1)那样的处理。那么这样处理之后电磁波还会保持正弦电磁波那样的特点吗?这就需要检验。图4和图5分别为当将正弦电场和磁场离散为200个取样点后,再用式(1)处理的结果。由图可以看出,其波仍保持着好的正弦特征,且电场幅度和磁场幅度之比正好等于波阻抗。

3.2 随机入射平面电磁波的等效源分布

本文中,分别将产生随机入射正弦平面电磁波的等效源的个数设置为 1、10、20、100、200 、300、400和500个,以便从结果中看出场分布与源的个数间的关系。在此,仅将源为500个时它们在球面上的分布示于图6中。当然,对它们具体位置的设置是按照2.1节中的约束条件选取的。其中,图6(a)为观察者位于球坐标θ=28°,φ=60°处的俯视图,图6(b)为观察者位于θ=32°,φ=23°处的俯视图。

从图中可以看出,波源在球面上的分布是随机均匀的,是满足统计规律要求的。

3.3 混响室内场分布仿真及数据分析

在此,以对尺寸为2.1 m×2.3 m×3.5 m的混响室的工作区域按90×90×90个网格划分后进行场分布仿真计算为例。对该区域内场的均匀性与哪些因素有关进行讨论。具体做法是,分别选择随机入射电磁波的个数为 1、10、20 、100 、200 、300 、400 和500个,计算区域内不同剖面层中的场分布,其结果以图示形式给出。限于文章篇幅,文中仅给出了yoz平面内的第45层,xoz平面内的第56层和xoy平面内的第68层的电场分布于图7的(a1)→(h1),(a2)→(h2)和(a3)→(h3)中。图中N表示重叠入射波的个数,网格从1→10、80→91代表吸收边界到连接边界的网格数。在yoz、xoz和xoy三个平面中的第45层、第56层和第68层的这三个层面是任意选取的。

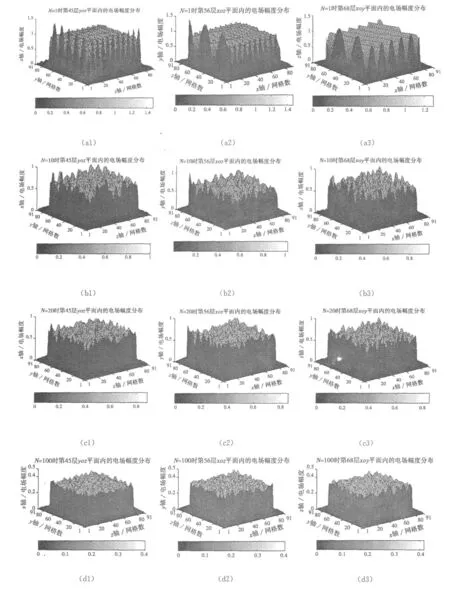
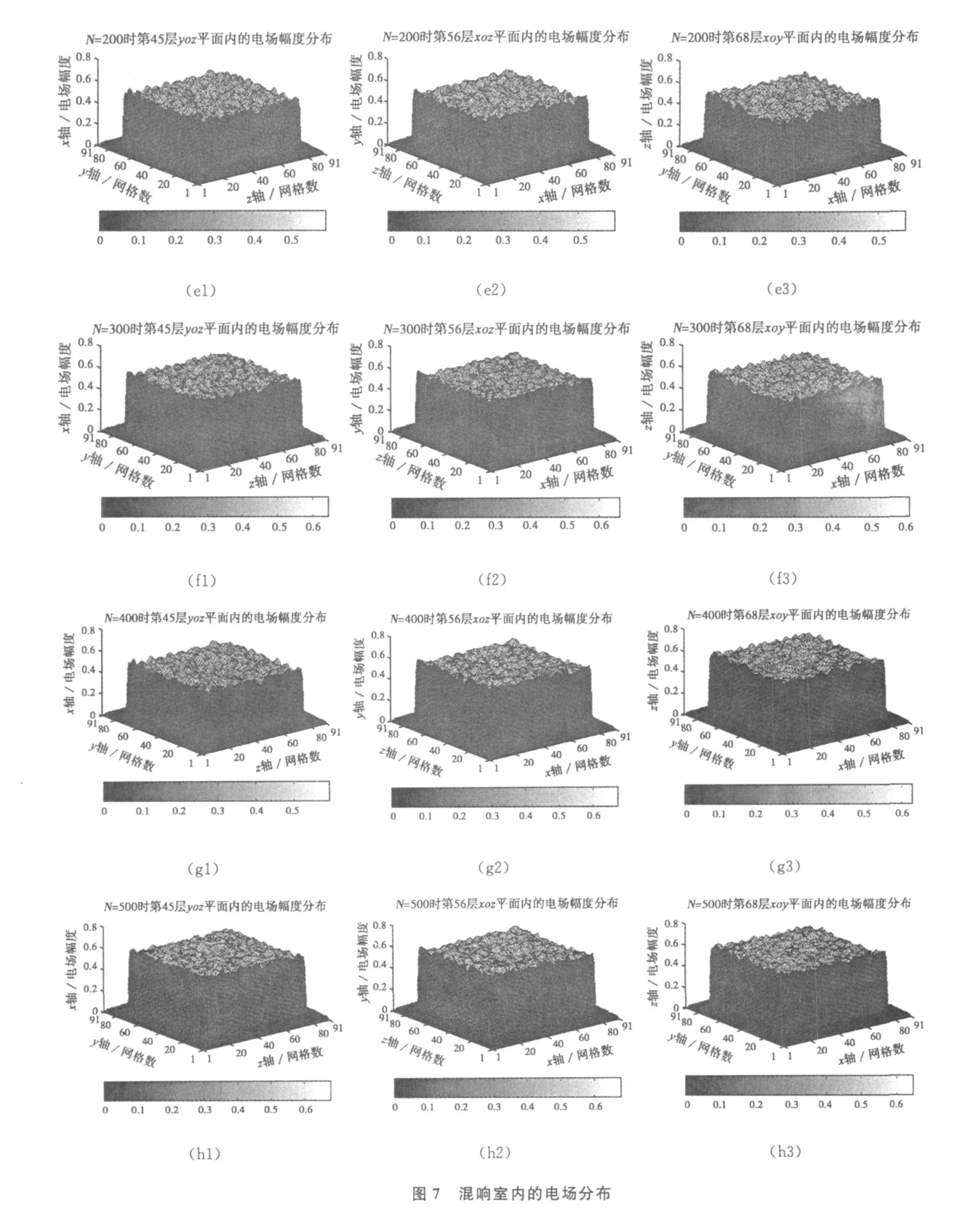
其中层数的划分是对90×90×90的计算区域进行的,每个坐标方向上均可化为90层,如图8所示,虚线正方体为计算区域。

图8 计算区域层数划分示意图

基于上述仿真结果并按照IEC61000-4-21标准中规定的计算方法就可以计算出混响室工作区域中的场均匀度,如表1所示。当入射波的个数为1时,电场强度的标准偏差为3.40 dB,它不满足标准中所提出的3 dB要求,并且可从图7的(a1)、(a2)和(a3)直观看出,此时场均匀性较差,它们的电场强度起伏较大,且包络为正弦规律,这就说明单个波入射的情况下混响室内场的均匀性较差;但随着入射电磁波数目的增加,比如,当入射波的个数大于或等于10时,标准偏差在小于3 dB的前提下逐渐减小,这表明场的均匀性越来越好,但与此同时,计算时间亦会逐渐增加,对计算机硬件的要求也同步提高。因此,对那些复杂的、要求精度高的问题在单个计算机不能处理或其消耗的时间相当长的情况下可采用并行算法进行求解。上述结果也提示人们,在对研究对象进行数值分析之前必须要依据问题的复杂性及其求解的精度要求,适当地选取入射波的个数,以达到既节约计算时间又满足求解精度的目的。

表1 频率为915 MHz时场的均匀性随入射波个数的变化

4.结 论

把重叠波理论运用到混响室的仿真分析中,使得计算时间只与测试体的特性相关,这样不仅能使仿真过程中混响室内的电磁环境与实际混响室内的电磁环境更接近,而且与传统的混响室仿真分析相比还可以大大缩短计算时间;同时,分析比较了不同重叠入射平面波情况下混响室内场分布的均匀度,得出了欲使混响室内场分布达到预设均匀度要求时,所应选取的最佳重叠入射平面波的数目,而本文工作中所表明的混响室内这种场分布的预期精度与应选取重叠入射平面波个数间的关系是文献[14]没有提及和体现的,从而为混响室的设计提供了可靠的理论指导。

[1] LEGNAB T,FREYER G,HATFIELD M,et al.Verification of fields applied to an EUT in a Reverberation chamber using numerical modeling[C]//IEEE Int.Symp.Electrom.Compatibility,1988,1：28-33.

[2] BONNET P,VERNET R,GIRARD S,et al.FDTD modeli-ng of reverberation chamber[J].Electronics Letters,2005,41(20)：1101-1102.

[3] BAI L,WANG L,WANG B,et al.Reverberation chamber modeling using FDTD[C]//IEEE Int.Symp.Electromagn.Compatibility,1999,1：7-11.

[4] CHUNG S Y,RHEE J G,RHEE H J,et al.Field unitormity characteristics of an asymmetric structure reverberation chamber by FDTD method[C]//IEEE Int.Symp.Electromagnetic Compatibility,2001,1：429-434.

[5] HARIM A K.FDTD analysis of electromagnetic fields in a reverberation chamber[J].IEICE Trans.Communication,1998,E81-B(10)：1946-1950.

[6] KOUVELIOTIS N K,TRAKADAS P T,CAPSALIS C N.Examination of field uniformity in vibration intrinsic reverberation chamber using the FDTD method[J].Electro.Letters,2002,38(3)：109-110.

[7] BUNTING C F.Statistical characterization and the simulation of a reverberation chamber using finite-element techniques[J].IEEE Trans.Electromagnetic Compatibility,2002,41(1)：214-221.

[8] BUNTING C F,MOELLER K J,REDDY C J,et al.A two-dimentional finite-element analysis of reverberation chambers[J].IEEE Trans.Electromagnetic Compatibility,1999,41(4)：280-289.

[9] HOEPPE F,GINESTE P,DEMOULIN B,et al.Numerical predictions applied to mode-stirred reverberation chambers[C]//Proc.Reverberation Chamber,Anechoic Chamber and OATS Users Meeting.Seattle,WA,2001.

[10] SURIANO C R,THIELE G A,SURIANO J R.Low frequency behavior of a reverberation chamber with monopole antenna[C]//IEEE Int.Symp.Electromagnetic Compatibility,2002,2：645-650.

[11] HILL D A.Plane wave integral representation for fields in reverberation chambers[J].IEEE Tran.E-lectromagnetic Compatibility,1998,40(3)：209-217.

[12] PETIRSCH M,SCHWAB A J.Investigation of the field uniformity of a mode-stirred chamber using diffusers based on acoustic theory[J].IEEE Transaction electromagnetic Compatibility,1999,41(4)：446-451.

[13] 沈远茂,石 丹,高攸纲,等.利用多天线源搅拌改善混响室场均匀性的分析[J].电波科学学报,2009,24(4)：682-686.SHEN Yuanmao,SHI Dan,GAO Yongang,et al.Improvement in field uniformity introduced by multiple-antenna in source-stirred reverberation chamber[J].Chinese Journal of Radio Science,2009,24(4)：682-686.(in Chinese)

[14]MOGLIEF,PASTORE A P.FDTDanalysis of plane wave superposition to simulate susceptibility tests in reverberation chambers[J].IEEE Trans.Electromagn.Compatibility,2006,48(1)：195-202.

[15] 葛徳彪,石守元,朱之伟.一种新的FDTD入射场设置方法[J].微波学报,1995,11(3)：187-190.GE Debiao,SHI Shouyuan,ZHU Zhiwei.A new FDTD scheme for introducing incident fields[J].Journal of Microwaves,1995,11(3)：187-190.(in Chinese)

[16] 葛德彪,闫玉波.电磁波时域有限差分方法[M].西安：西安电子科技大学出版社,2005：14-20.