一种快速计算雷达散射截面空域特性的方法

凌 劲 龚书喜 王文涛 王 兴 张玉洁

(西安电子科技大学天线与微波技术重点实验室，陕西 西安 710071)

1.引 言

矩量法(MoM)是求解电磁问题的经典数值算法[1]，在准确求解任意形状三维导体的雷达散射截面(RCS)方面有着十分广泛的应用。阻抗矩阵的填充和求解是矩量法中两个计算量比较大的操作。目标的雷达散射截面与频率f和角度(θ,φ)均有关系，采用MoM就必须在频带和角域内同时或分别求解矩阵方程。采用MoM逐点计算时，必须以一定的频率和角度间隔在所给定的频率和角域内逐点反复求解矩阵方程。当目标的感应电流分布随频率或入射角变化剧烈时，必须很小的频率或角度间隔计算才能得到精确的结果，这意味着在整个频带或角域内矩阵方程求解次数的增加，势必将占用了大量的计算时间和内存。近年来，渐近波形估计(AWE)技术被逐渐应用到电磁场的全波分析[2-5]。与MoM逐点计算相比，它们可以在计算频点比较多的时候节省较多的时间，但该方法有效的计算频带受到Taylor级数和padé逼近本身性质的限制。利用AWE技术可以确定展开点附近的值，这时应用AWE方法得到的解是精确的。但是随着频率逐渐远离展开频率点，解的精确度也就逐渐下降，而且计算过程中需要计算和存储稠密的阻抗矩阵及其高阶导数矩阵，占用了大量内存。与传统的矩量法程序相结合时，AWE技术中关于阻抗矩阵元素的求导运算增加了程序编写的复杂度。Maehly逼近[6-7]结合矩量法已成功用于计算雷达散射截面的频率响应[8-9]。Maehly逼近与AWE技术相比，最大的优势在于Maehly逼近不需要计算阻抗矩阵元素的高阶导数，减小了程序编写的复杂度，很容易和MoM计算机代码相结合。与AWE技术中padé逼近相比，在相同阶数的情况下，Maehly逼近能在更宽的频带内很好地与MoM计算结果相吻合。虽然文献[10][11]应用二维AWE技术分析了目标雷达散射截面的空频二维特性(频率f和角度θ同时外推)，但该方法有效的计算频带和角域受到AWE技术本身性质的限制，然而对目标雷达散射截面的角度θ和φ同时外推的研究在文献中还很少见到。基于以上考虑，将Maehly逼近引入到目标雷达散射截面的角度外推中，分析雷达散射截面空域二维特性。将Maehly逼近推广成二维外推技术，应用于快速分析雷达散射截面的空域特性(θ和φ的同时外推)。

2.理论分析

2.1 基于EFIE的矩量法

根据导体表面S及线天线上切向电场连续条件，可得电场积分方程(EFIE)

-Etan(r)=[-jωA(r)-▽Φ(r)]tan

(1)

式中：Etan(r)是入射场；A(A)，Φ(r)分别表示磁矢位和电标位。采用伽略金法，基函数和检验函数都为RWG基函数[12]，可得式(1)的矩阵形式

[Zmn(k)]·[In(k，θ，φ)]=[Vm(k，θ，φ)]

(2)

式中：In(n=1, 2,…,N)为未知感应电流的展开系数，N为RWG基函数个数； [Zmn]和[Vm]分别是阻抗矩阵和激励矩阵；k为自由空间的波数；θ和φ为入射角。通过解矩阵方程(2)可以得到表面感应电流的分布，进而可以计算得出雷达散射截面σ.

(3)

若采用传统矩量法求解，则需要在给定的角域内[θ1,θ2]和[φ1,φ2]逐点扫描反复求解矩阵方程(2)，势必导致巨大的计算量，占用大量的计算时间。

2.2 二维外推技术

文献[8]-[9]中Maehly逼近结合矩量法只用于了快速计算雷达散射截面的频率响应，无法获得雷达散射截面的二维特性。因此，将其扩展成二维外推技术对目标雷达散射截面的角度θ和φ进行同时外推，快速计算雷达散射截面的空域二维特性。Maehly逼近结合矩量法的基本思想是在给定的角域内，通过坐标变换可得关于角度θ和φ的切比雪夫节点。采用矩量法求解电场积分方程，计算出这些切比雪夫节点处的表面感应电流，从而获得该角域内表面感应电流的切比雪夫多项式(又名最佳一致多项式逼近)[13]，并通过Maehly逼近将切比雪夫多项式转化为有理函数，由此获得任意入射角度时的表面感应电流分布。对给定的角域θ∈[θ1,θ2]和φ∈[φ1,φ2]作坐标变换可得

(4)

(5)

(6)

(7)

式中，Lθ，Lφ，Mθ和Mφ分别表示零点和极点的展开阶数。

(8)

利用切比雪夫多项式的恒等式

(9)

则

(10)

(11)

把式(11)代入式(8)可得

(12)

(13)

(14)

3.实验结果分析

一金属平板(2λ×2λ)挖有三个圆孔(r1=0.15λ,r2=0.25λ,r3=0.7λ)，一φ极化平面波入射。平板表面被剖分成692个三角面片，一共N=951个未知量。采用Maehly逼近结合MoM，AWE技术和MoM分别计算了该平板在φ=0°时的单站RCS随入射角度θ的变化情况，计算结果如图1所示。AWE技术以θ=45°作为展开点，1°为计算间隔。由图1可知，AWE技术有效的计算角域约为22°～69°，而Maehly逼近结合MoM能在整个角域内(0°～90°)很好地逼近MoM逐点计算的结果。

与AWE技术中padé逼近相比，在取相同阶数的情况下，Maehly逼近能在更宽的角域内很好地与MoM计算结果相吻合。在θ(-90°～90°)和φ(0°～360°)内观察该平板的单站RCS随入射角θ和φ的变化情况。图2给出了采用本文的Maehly逼近(Lφ=9,Mφ=9,Lθ=9,Mθ=9)结合MoM计算的该平板二维散射特性。当取L=M或L=M+1时误差将最小[2]。将φ分别等于0°，30°，45°，60°时Maehly逼近结合MoM计算的结果与MoM逐点计算结果进行了比较，计算间隔为1°，如图3所示。不同角度入射时Maehly逼近结合MoM与MoM逐点计算结果吻合良好。Maehly逼近和MoM逐点计算时间分别为146 min和1910 min。由此可见：应用最佳一致有理逼近理论结合矩量法分析目标雷达散射截面的空域二维特性，使得计算效率大大提高。

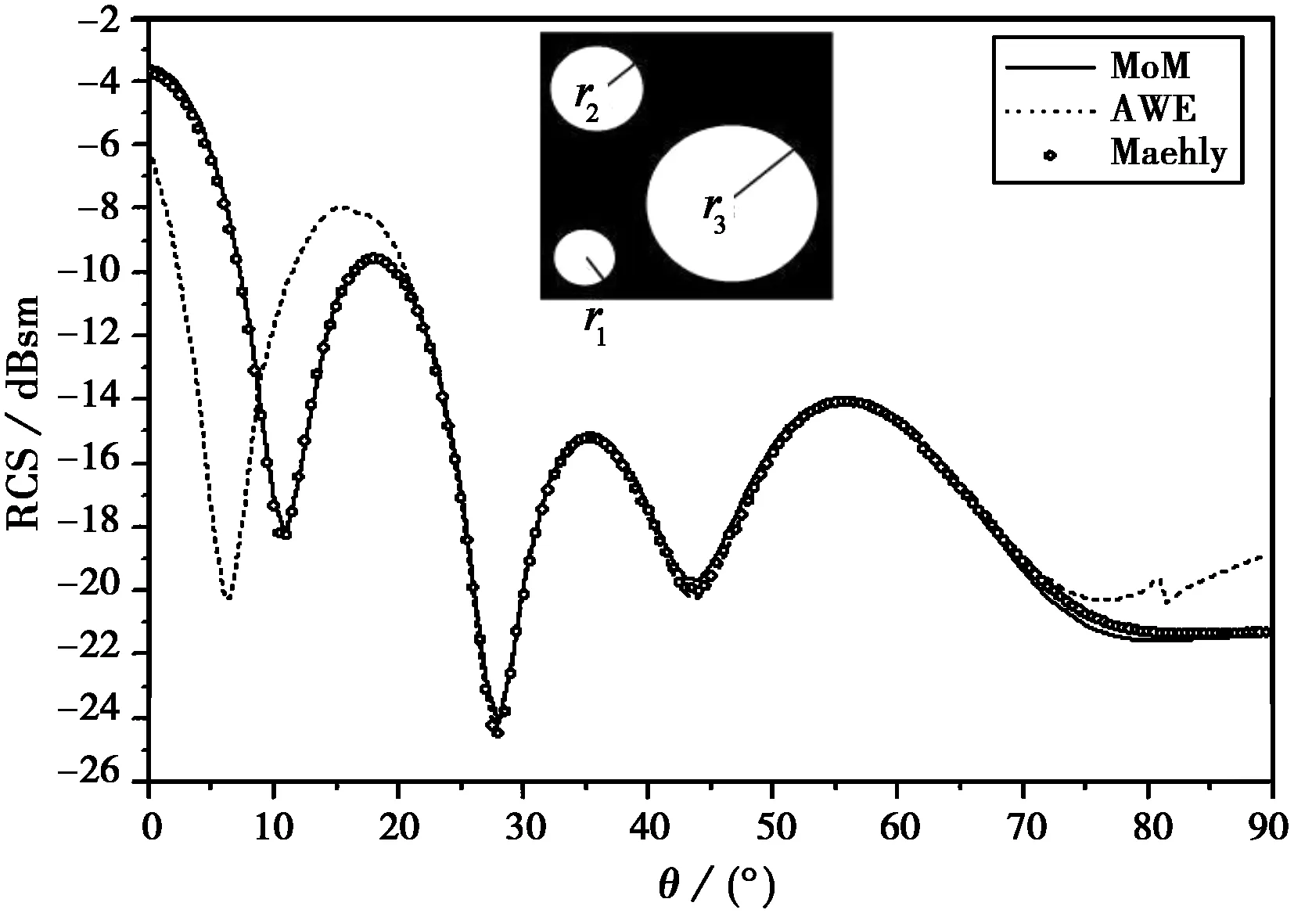
图1 RCS随入射角度θ变化

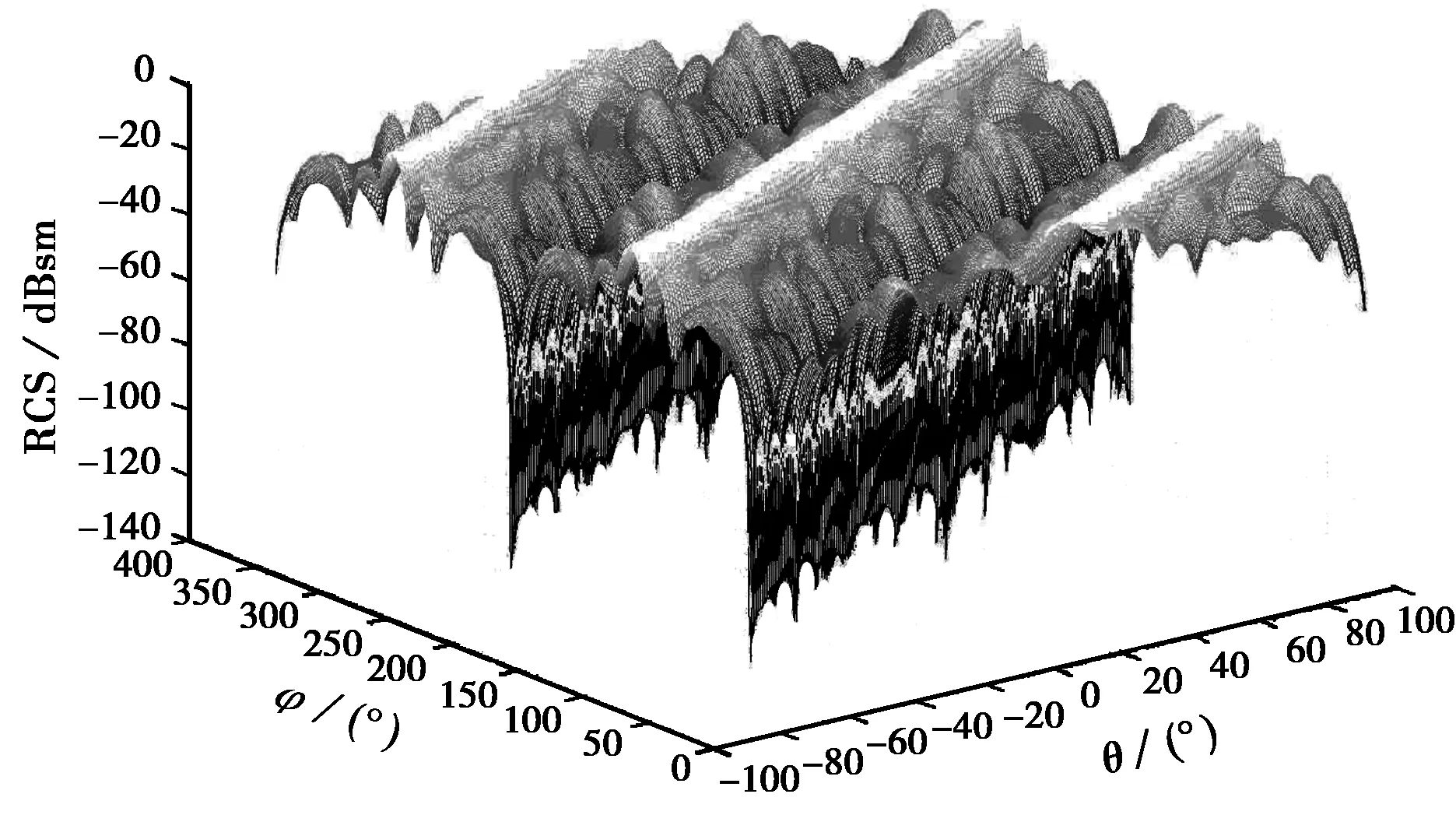
图2 平板的单站RCS

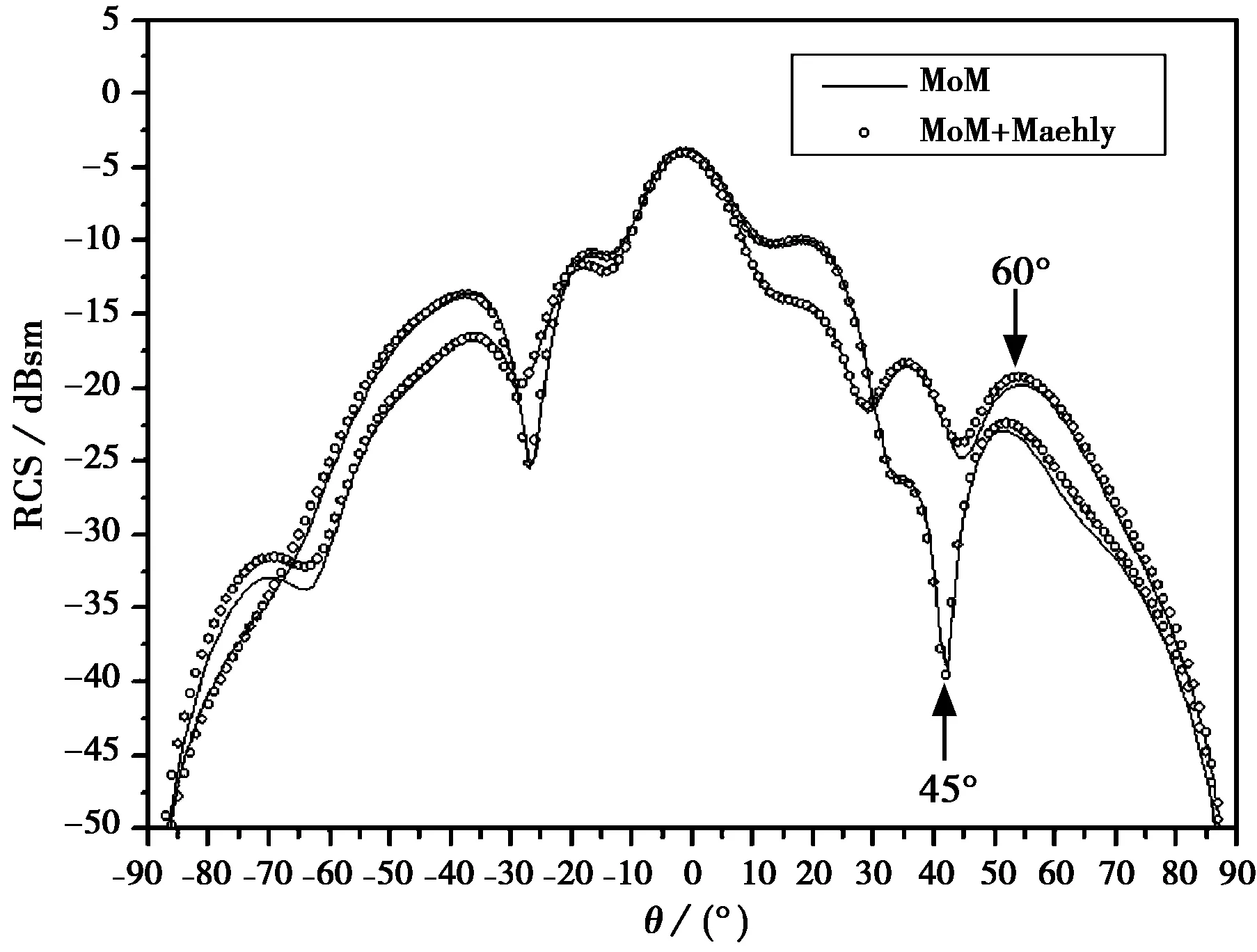
图3 RCS随入射角度θ变化

一去掉底面的圆锥体高为1.0λ，底面半径为0.5λ。组合体表面被剖分成637个三角面片，一共N=937个未知量。φ极化平面波入射，采用本文的Maehly逼近(Lφ=9,Mφ=9,Lθ=9,Mθ=9)结合MoM分析圆锥体随入射角度θ和φ同时变化的二维散射特性，计算的单站RCS如图4所示。由于圆锥体的对称性，只考察了θ从-90°～90°和φ从0°～180°之间的变化。将φ分别等于0°，30°，45°，60°时的结果与MoM逐点计算结果进行了比较，计算间隔为1°，如图5所示。Maehly逼近结合MoM和MoM逐点计算时间分别为122 min和1754 min。与矩量法的计算时间相比，该方法大大节省了计算机耗时。从图5可以看出，不同角度入射时采用Maehly逼近结合MoM完全能逼近MoM逐点计算的结果，并且有效地提高了计算效率，数值结果证明了该方法的有效性。

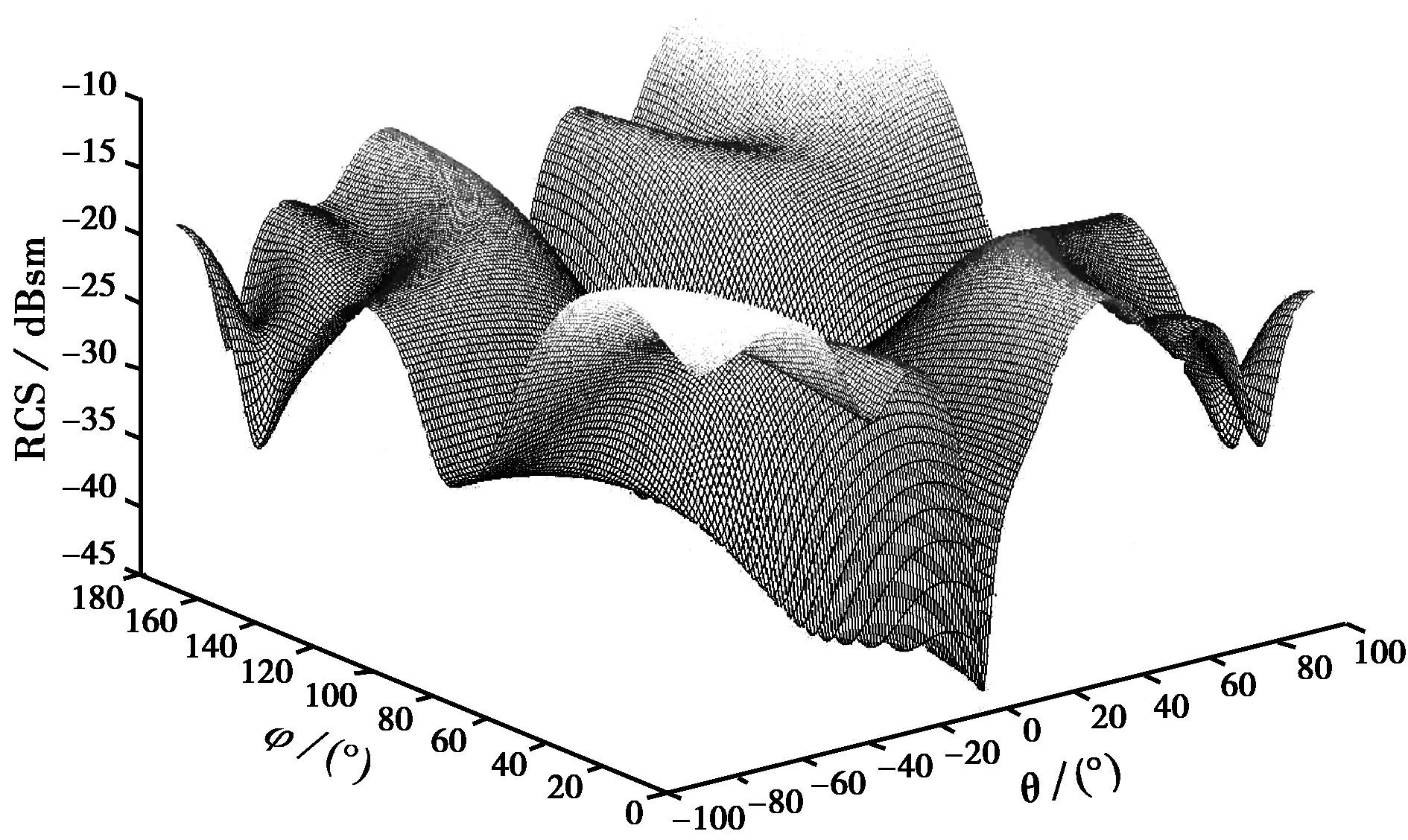
图4 圆锥体的单站RCS

图5 圆锥体RCS随入射角度θ变化

4. 结 论

本文介绍了Maehly逼近结合矩量法在目标雷达散射截面的角度外推中的应用，将Maehly逼近推广成二维外推技术，应用于目标雷达散射截面角度(θ和φ)的同时外推，数值结果证明了该方法的有效性。Maehly逼近结合MoM的结果与MoM逐点计算结果非常吻合，该方法能有效提高计算效率。

[1] HARRINGTON R F. Field computation by moment methods[M]. IEEE Press, New York, 1993.

[2] REDDY C J, DESHPANDE M D, COCKRELL C R, et al. Fast RCS computation over a frequency band using method of moments in conjunction with asymptotic waveform evaluation technique[J]. IEEE Transactions on Antennas and Propagation, 1998, 46(8): 1229-1233.

[3] ERDEMLI Y E, GONG J, REDDY C J, et al. Fast RCS pattern fill using AWE technique[J]. IEEE Transactions on Antennas and Propagation, 1998, 46(11): 1752-1753.

[4] 刘芸江, 甄蜀春, 李 曼, 等. AWE技术结合矩量法分析某型八木天线[J]. 电波科学学报, 2003, 18(3): 337-340.

LIU Yunjiang, ZHEN Shuchun, LI Man, et al. A new technical for analyzing a YagiAntenna based on the MOM in conjunction with AWE technique[J]. Chinese Journal of Radio Science, 2003, 18(3): 337-340. (in Chinese)

[5] 秦建军, 殷兆伟, 曹祥玉, 等. 渐进波形估计技术在线天线分析中的应用[J]. 电波科学学报, 2005, 20(6): 824-828.

QIN Jianjun, YIN Zhaowei, CAO Xiangyu, et al. Applications of asymptotic waveform evaluation technique in the analysis of wire antenna[J]. Chinese Journal of Radio Science, 2005, 20(6): 824-828. (in Chinese)

[6] MAEHLY H J. Rational approximations for transcendental functions[C]//Proceedings of the International Conference on Information Processing. UNESCO, Butterworths, London, 1960.

[7] 王仁宏. 数值有理逼近[M]. 上海: 上海科学技术出版社, 1980.

[8] CHEN M S, WU X L, HUANG Z X, et al. Accurate computation of wideband response of electromagnetic scattering problems via Maehly approximation[J]. Microwave and Optical Technology Letters, 2007, 49(5): 1144-1146.

[9] CHEN M S, WU X L, SHA W, et al. Fast and accurate radar cross-section computation over a broad frequency band using the best uniform rational approximation[J]. IET Microwave Antennas Propagation, 2008, 2(2): 200-204.

[10] TONG C M, HONG W, YUAN N C. Simultaneous extrapolation of RCS in both angular and frequency domains based on AWE technique[J]. Microwave and Optical Technology Letters, 2002, 32(2): 290-293.

[11] 童创明, 高 阳, 卢 燕, 等. 一种新的雷达目标散射截面宽带和宽角同时外推技术[J]. 电波科学学报, 2007, 22(5): 790-793.

TONG Chuangming, GAO Yang, LU Yan, et al. A new extrapolation technique of RCS in both angular and frequency domains[J]. Chinese Journal of Radio Science, 2007, 22(5): 790-793. (in Chinese)

[12] RAO S M, WILTON D R, GLISSON A W. Electromagnetic scattering by surfaces of arbitrary shape[J]. IEEE Transactions on Antennas and Propagation, 1982, 30(5): 409-418.

[13] MASON J C, HANDSCOMD D C. Chebyshev polynomials[M]. CRC Press LLC, New York, 2000.