基于镜面散射的雷达探测浅海水下地形研究

王 珂 洪 峻 明 峰 丁 岩

(1.中国科学院空间信息处理与应用系统技术重点实验室，北京 100190； 2.中国科学院电子学研究所，北京 100190；3.中国科学院研究生院，北京 100049)

1． 引 言

雷达可遥感探测浅海水下地形，可实现对浅海地质环境的快速、动态、大范围监测，对此国外已开展了大量的理论和实验研究[1-3]，但其主要是基于布拉格(Bragg)共振散射模型的。Hennings I[4-6]对基于高斯分布的海面镜面散射模型的雷达探测浅海水下地形机制，进行了理论研究，并利用船载雷达进行了实验验证。小入射角时雷达海洋遥感，需要掌握海面镜面散射建模及其应用方法。对于海面镜面散射建模，国外学者已有了一些研究[7-9]，但有关Gram-Charlier分布在镜面散射建模中的性能及其在海洋遥感中的应用效果，却少有论述。首先建立了基于Gram-Charlier分布的海面镜面散射模型，深入研究其性能表现，为由海面镜面散射产生的雷达后向散射截面，提供了定量计算方法。其次，验证了基于Gram-Charlier分布的海面镜面散射模型在中低风速时性能可靠后，将其应用于雷达探测浅海水下地形。为基于海面镜面散射模型的雷达海洋遥感，提供了理论验证和应用方法。

2. 理论与模型

2.1 海面镜面散射理论

海面电磁波的散射机制，按入射角范围，主要分为[7,10]：镜面散射和Bragg共振散射。在海面风场作用下，波浪可发生相对于水平面大至25°的倾斜[11]，则雷达入射角小于20°时，主要是由镜面散射产生了雷达后向散射截面[7]。

Valenzuela G R[7]提出当海面斜率为各向同性高斯分布时，可计算海面镜面散射产生的雷达后向散射截面为

(1)

式中：θ为雷达入射角；R(0)为雷达波垂直入射时(θ=0°)的菲涅耳(Fresnel)反射系数；s2为总的海面均方斜率。

经典理论认为：镜面散射正比于海面斜率的概率密度函数[7]。目前海面斜率分布有三种：高斯分布、Gram-Charlier分布、Liu Y分布[12]。Cox C和Munk W用航空拍摄海面太阳耀斑的方法测量了海面斜率的实际分布[11]，提出海面斜率可服从Gram-Charlier分布。Liu Y分布在高风速时比Gram-Charlier分布性能更好。但Liu Y分布没有给出其中峰度系数n和偏度系数λsk随连续风速的取值方法[12]，严重限制了其实际应用。为了计算在不同雷达和海况条件连续输入下，由海面镜面散射产生的σ0，建立了基于Gram-Charlier分布的海面镜面散射模型。

2.2 基于Gram-Charlier分布的海面镜面散射模型

Barrick D E[13]提出的随机粗糙表面镜面散射模型，可用于计算由海面镜面散射产生的雷达后向散射截面[7],即

σ0=πsec4θ|R(0)|2p(ζx,ζy)

(2)

式中：θ为雷达入射角；R(0)为雷达波垂直入射时(θ=0°)的Fresnel反射系数；p(ξx,ξy)为海面x方向斜率ζx和y方向斜率ζy的联合概率密度函数。

假设在海面上存在确定坐标系(x,y)，y轴的正向指向逆风方向；x轴的正向指向为y轴正向顺时针旋转90°，即侧风方向。根据入射雷达波在海面倾斜波面上发生镜面散射时的几何光学关系[11,13]，对于产生镜面散射的海面斜率，则有

ζx=tanθsinφ

(3)

ζy=tanθcosφ

(4)

式中：θ为雷达入射角；φ为雷达波与逆风方向之间的夹角，φ=0°时雷达波指向逆风方向。

对于海面斜率的Gram-Charlier分布[11]，即有

c04(η4-6η2+3)]}

(5)

其中，逆风(up-wind)和侧风(cross-wind)方向上的海面均方斜率规范化为

(6)

(7)

Cox C和Munk W由实测数据，给出了逆风和侧风方向上的海面均方斜率为

(8)

(9)

式中,u12.5为海面上12.5 m高度的风速。

总的海面均方斜率为

(10)

Wu J[14]对Cox C和Munk W的实测数据，重新进行了统计，给出了更为准确的表达

s2= (0.90+1.20·Inu10)×10-2

(u10<7 m/s)

(11)

s2= (-8.40+6.00·Inu10)×10-2

(u10>7 m/s)

(12)

且有如下近似关系

(13)

偏度系数为

c21=m-nu12.5

(14)

c03=p-qu12.5

(15)

而c40、c22、c04为峰度系数。式(2)～(15)中的参数，取清洁水体(clean surface)时[11]，如表1所示。

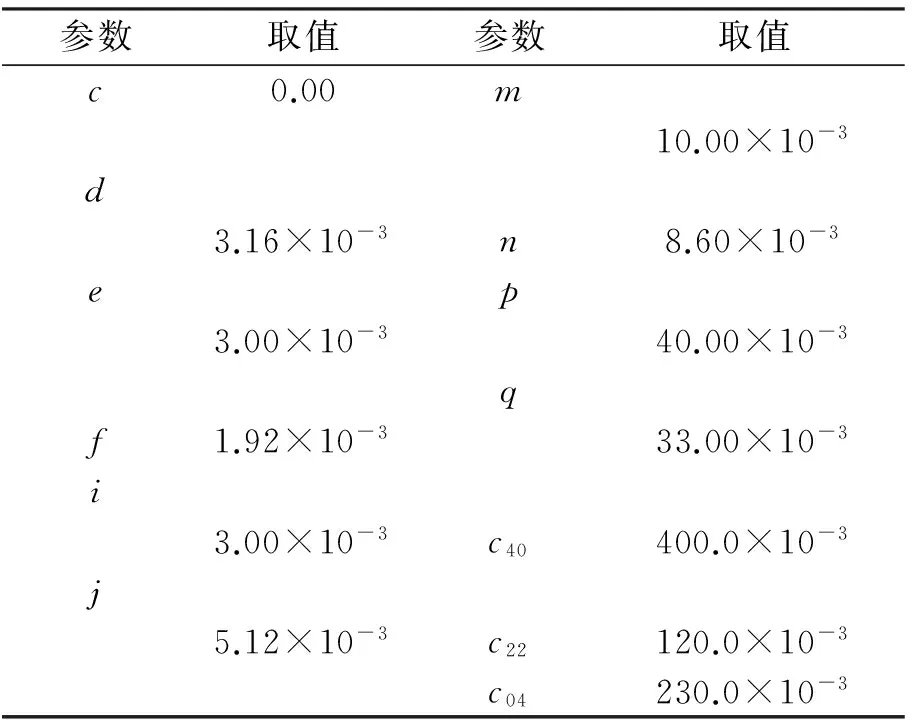
表1 Gram-Charlier分布中的参数取值

对于电磁波的镜面散射可有[13]

(16)

(17)

RVH(0)=RHV(0)→0

(18)

式中：εr为海水的相对介电常数，与雷达波段有关[15]；μr为海水的相对磁导率，可取μr=1，代入式(16)、(17)，则有RVV(0)=RHH(0)； 下标VV、HH等表示极化。所以可取

|R(0)|2=|RVV(0)|2=|RHH(0)|2

(19)

将式(16)～(19)代入式(2)可见

(20)

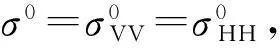
2.3 风速的统一

风速在实际使用时，通常是以海面上10 m高度的u10为基准，所以需将u12.5换算为u10。在大气中性稳定的情况下，摩擦风速u*与风速的关系为

(21)

式中：uz为海面上z(m)高度处的风速；κ为冯·卡门(von Karman)常数；z0为粗糙长度，可由下式计算[3]

(22)

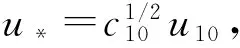
c10=(0.8+0.065u10)×10-3

(23)

综合式(21)～(23)，在模型中风速将统一由u10表示，以减少选取风速时带来的误差。

2.4 雷达探测模型

根据Hennings I[6]的理论探讨，在u10≤8 m/s时应用Gram-Charlier分布的雷达探测浅海水下地形应具有可行性。典型浅海水下地形如图1所示，为锯齿状沙坡，设地形梯度方向为xperp方向。

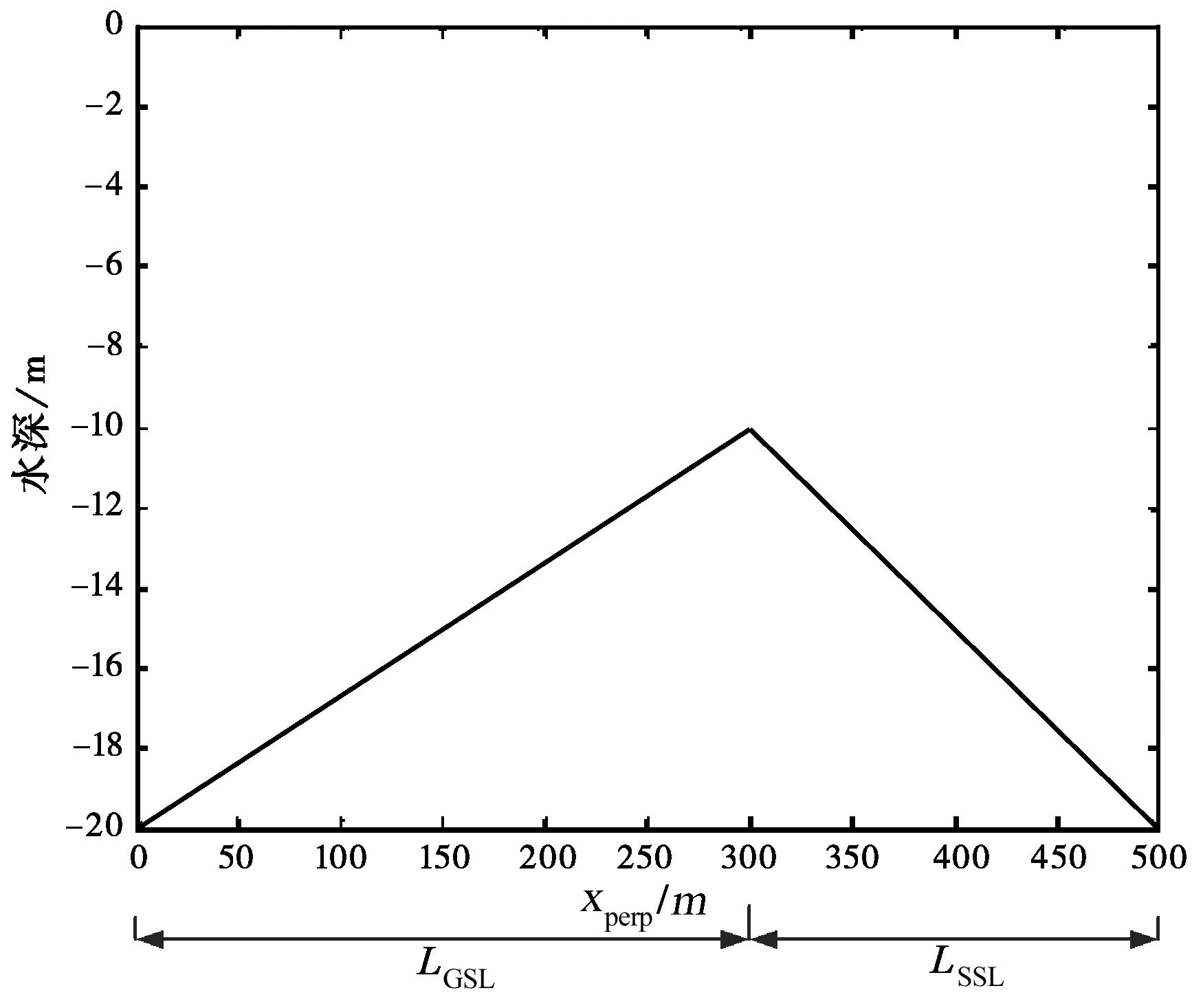
图1 典型浅海水下地形示意图

能量谱F(k)与作用量谱N(k)和波高谱Ψ(k)的关系为[16]

(24)

式中：g为重力加速度；k为波数，固有频率为

ω′=(gk)1/2

(25)

可取波高谱的形式为[17]

Ψ(k)=apk-4

(26)

式中，ap是菲利普斯(Phillips)常数。Stolte S[18]经测量给出了ap与风速(u10≤8 m/s时)的关系为

log10ap= -2.90+3.06·10-1u10-

(27)

水下地形对能量谱(假设潮流流经水下地形之前处于谱平衡状态F0)的一阶扰动调制为[1，4-5]

(28)

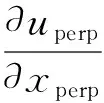
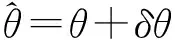
(29a)

(29b)

(29c)

(29d)

(29e)

对于真实的粗糙海面，有效入射角可重写为

θ=θplane+θrough

(30)

式中,θplane为平坦海面时的入射角，粗糙海面引起的入射角可表示为

tan2θrough=s2

(31)

被水下地形扰动的入射角，可由下式得到

(32a)

(32b)

能量谱与海面均方斜率的关系为[17]

(33)

所以有

(34)

(35)

式中： 波数的积分区间为k0=2π/λ0≤k≤kc=2π/λradar,λ0为雷达空间分辨率，λradar为雷达波长；α是逆风方向与xperp方向上潮流分量之间的夹角。

由式(3)、(4)，被水下地形扰动的海面斜率为

δζx=tanδθ·sinφ

(36)

δζy=tanδθ·cosφ

(37)

由式(6)、(7)，被水下地形扰动后，规范化的海面均方斜率可重写为

(38)

(39)

综合式(24)～(39)代入式(2)，可得水下地形扰动引起的雷达后向散射截面的变化为

δσ=σ-σ0

π·|R(0)|2·sec4(θ)·p(ζx,ζy)

(40)

则水下地形扰动对雷达后向散射截面的调制为

(41)

3. 实验与分析

3.1 海面镜面散射模型的实验分析

为了验证基于Gram-Charlier分布的海面镜面散射模型的正确性，并研究其性能，给出了其与基于高斯分布时(即式(1))的实验比较，如图2～5所示。模型计算的σ0，与Plant W J[8]的Ku波段实测数据和CMOD4模型[19]数据(可表示C波段实测的σ0[12])相比较。

图2是Ku波段，u10=8 m/s，θ=10°时基于Gram-Charlier分布和高斯分布，其中采用Wu J方法估计海面均方斜率，分别计算的σ0，与Plant W J实测数据相比较。可见，基于Gram-Charlier分布计算的σ0，总体上能合理地反映镜面散射随风向的变化，更接近实测数据；相比基于高斯分布时具有一定优越性。

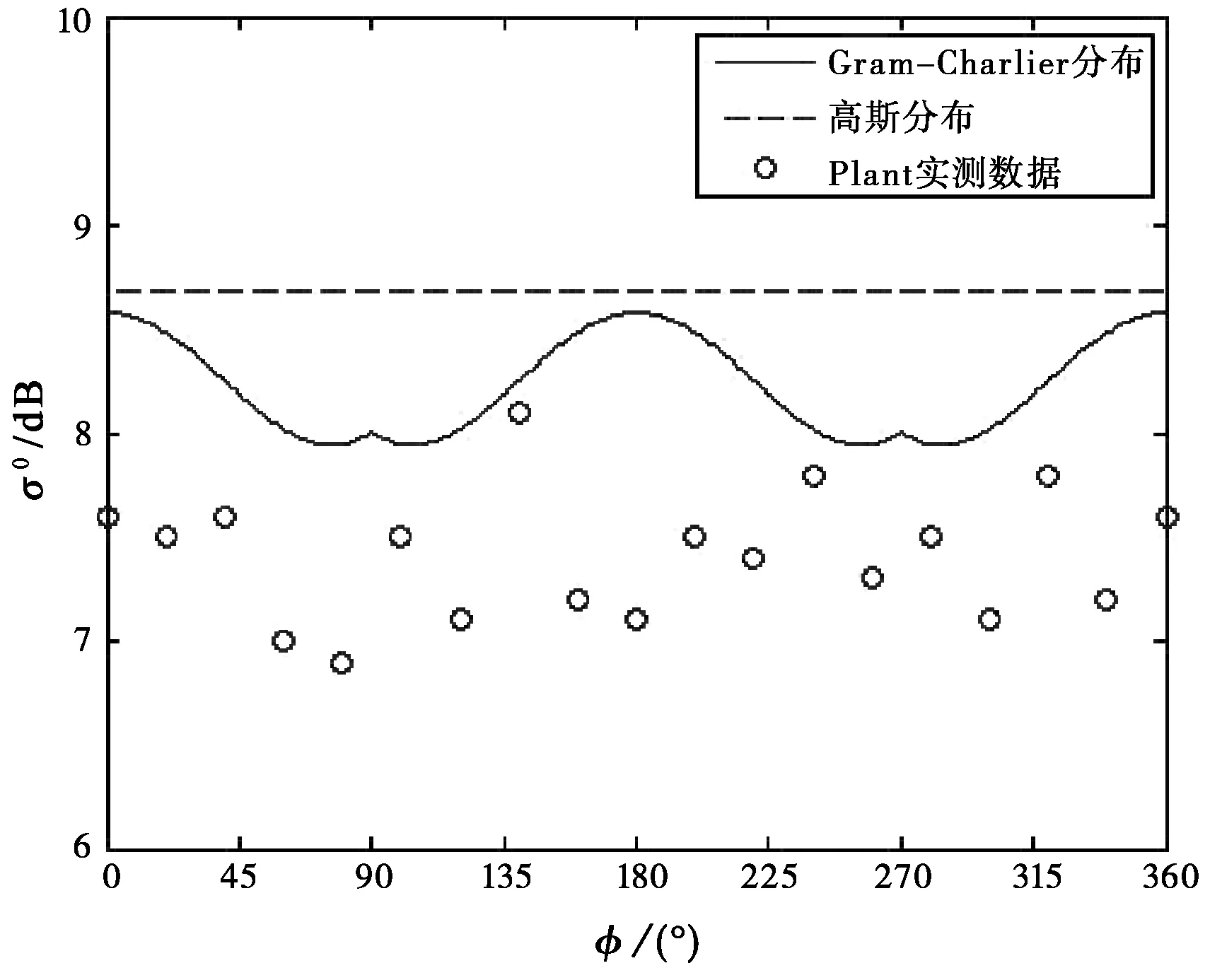
图2 Ku波段，u10=8 m/s，Wu J方法

图3是C波段，u10=8 m/s，θ=16°时基于Gram-Charlier分布和高斯分布，采用Wu J方法估计海面均方斜率，分别计算的σ0，与CMOD4模型数据相比较。可获得与图2中同样的结论。

图3 C波段，u10=8 m/s，Wu J方法

图4是C波段，u10=2 m/s，θ=16°时基于Gram-Charlier分布和高斯分布，采用Cox C和Munk W方法估计海面均方斜率，分别计算的σ0，与CMOD4模型数据相比较。可见，两种镜面散射模型计算的σ0，均有较大误差；特别是基于Gram-Charlier分布时，在侧风方向(φ=90°)计算的σ0大于逆风方向(φ=0°)。还将Ku波段，u10=2 m/s，θ=10°时基于Gram-Charlier分布，采用Cox C和Munk W方法估计海面均方斜率，计算的σ0，与Plant W J实测数据进行了比较，出现了同样的问题。这明显不符合Plant W J由实测数据，获得的σ0随风向的“类余弦”变化规律。

图5是C波段，u10=2 m/s，θ=16°时，基于Gram-Charlier分布和高斯分布，采用Wu J方法估计海面均方斜率，分别计算的σ0，与CMOD4模型数据相比较。可见，采用Wu J方法估计海面均方斜率，改进了两种镜面散射模型的性能表现，计算的σ0更接近实测数据。还将Ku波段，u10=2 m/s，θ=10°时基于Gram-Charlier分布，采用Wu J方法估计海面均方斜率，计算的σ0，与Plant W J实测数据进行了比较，出现了同样的改进效果。

图4 C波段，u10=2m/s，Cox C、Munk W方法

图5 C波段，u10=2 m/s，Wu J方法

研究基于Gram-Charlier分布的海面镜面散射模型的性能时，发现导致其偏差的主要原因是Cox C和Munk W估计的海面均方斜率、峰度系数、偏度系数有一定的误差范围，可用“±标准差”来表示[11]。通过实验分析，认为采用Wu J方法估计海面均方斜率， 可改进Gram-Charlier分布在中低风速时的性能，以减少σ0的计算误差。但发现改进后模

型的准确性仍与风速条件有关， 过高风速时(u10>14 m/s)会引起基于Gram-Charlier分布的建模偏差增大，这与Liu Y的分析相符合[12]。而通过与CMOD4模型数据的比较，发现过低风速时(u10<2 m/s)也有较大的建模偏差。所以认为模型需要首先进行风速条件下的验证，以避免应用时出现错误。通过与Plant W J实测数据和CMOD4模型数据的比较，采用Wu J方法估计海面均方斜率，将风速统一为u10，在中低风速(u10=(2～8)m/s)范围内，基于Gram-Charlier分布的海面镜面散射模型性能可靠。

3.2 雷达探测的实验分析

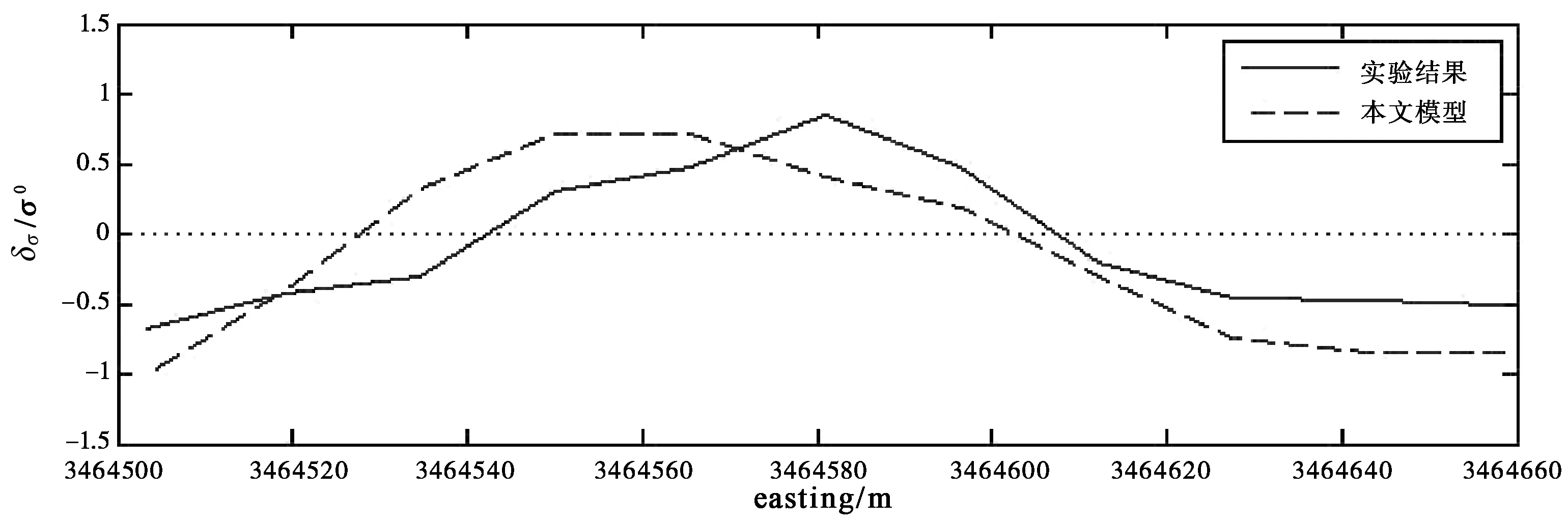
图6 浅海水下地形对雷达后向散射截面的调制

4. 结 论

深入研究了基于Gram-Charlier分布的海面镜面散射建模方法，分析了其极化特性，将风速统一以海面上10 m高度为基准，以减少选取风速时带来的误差。通过与实测数据的比较，证明了基于Gram-Charlier分布的海面镜面散射模型的正确性，及相比基于高斯分布时具有优越性，特别是明确地给出了σ0随风向的变化。提出了采用Wu J方法估计海面均方斜率，可改进Gram-Charlier分布在中低风速时的性能，以减少σ0的计算误差。指出了过高(u10>14 m/s)或过低(u10<2 m/s)的风速均会引起建模偏差的增大，并分析了其原因。提出了基于Gram-Charlier分布的海面镜面散射模型在应用时，需要首先进行风速条件下的验证，以避免出现错误，这是Hennings I[6]未曾考虑到的问题。进而将基于Gram-Charlier分布的海面镜面散射模型应用于雷达探测浅海水下地形，通过与实验结果的比较，证明了其可行性和优越性。对Gram-Charlier分布在海面镜面散射建模中的性能，及其在雷达探测浅海水下地形中应用方法的研究，一方面为海面镜面散射提供了定量计算方法；另一方面为基于海面镜面散射模型的遥感探测提供了理论验证和应用方法，获得的结论对实际应用有指导作用。由于Hennings I理论是一阶模型[4-6]，其准确性有限，适用条件也有待更多的实验验证，这将是以后的研究方向。

[1] ALPERS W, HENNINGS I. A theory of the imaging mechanism of under water bottom topography by real and synthetic aperture radar[J]. Journal of Geophysical Research, 1984, 89(6): 10529-10546.

[2] HENNINGS I. A historical overview of radar imaging mechanism of sea bottom topography[J]. International Journal of Remote Sensing, 1998, 19(7): 1447-1454.

[3] VOGELZANG J. Mapping submarine sand waves with multiband imaging radar 1.Model development and sensitivity analysis[J]. Journal of Geophysical Research, 1997, 102(C1): 1163-1181.

[4] HENNINGS I, HERBERS D. Radar imaging mechanism of marine sand waves at very low grazing angle illumination caused by unique hydrodynamic interactions[J]. Journal of Geophysical Research, 2006, 111(C10): C10008. doi:10.1029/2005JC003302.

[5] HENNINGS I, HERBERS D. Radar imaging mechanism of marine sand waves at very low grazing angle illumination[C]//EARSeL eProceedings, 2005, 4: 226-240.

[6] HENNINGS I, HERBERS D. The expected potential of TerraSAR-X high resolution spotlight mode data for shallow sea bottom topography imaging:a preview[C]//EARSeL eProceedings, 2007, 6: 67-81.

[7] VALENZUELA G R. Theories of the interaction of electromagnetic and ocean waves-a review[J]. Boundary-Layer Meteorology, 1978, 13: 61-85.

[8] PLANT W J. A stochastic, multiscale model of microwave backscatter from the ocean[J]. Journal of Geophysical Research, 2002, 107 (C9): 3120. doi:10.1029/2001JC000909.

[9] FREILICH M H, VANHOFF B A. The relationship between winds,surface roughness,and radar backscatter at low incidence angles from TRMM precipitation radar measurements[J]. Journal of Atmospheric and Oceanic Technology, 2003, 20(4): 549-562.

[10] 邵连军, 张训械, 孙 强, 等. GPS信号海面散射特性和初步实验结果[J]. 电波科学学报, 2008, 23(4): 699-703.

SHAO Lianjun, ZHANG Xunxie, SUN Qiang, et al. Property of GPS signal scattered from sea surface and preliminary experimental results[J]. Chinese Journal of Radio Science, 2008, 23(4): 699-703. (in Chinese)

[11] COX C, MUNK W. Measurement of the roughness of the sea surface from photographs of the sun's glitter[J]. Journal of the Optical Society of America, 1954, 44(11): 838-850.

[12] LIU Y, YAN X H, LIU W T, et al. The probability density function of ocean surface slopes and its effects on radar backscatter[J]. Journal of Physical Oceanography, 1997, 27(5): 782-797.

[13] BARRICK D E. Rough surface scattering based on the specular point theory[J]. IEEE Transactions on Antennas and Propagation, 1968, AP16(4): 449-454.

[14] WU J. Mean square slopes of the wind-disturbed water surface,their magnitude, directionality,and composition[J]. Radio Science, 1990, 25(1): 37-48.

[15] ULABY F T, MOORE R K, FUNG A K. Microwave Remote Sensing[M]. MA: Artech House, 1986: Vol.Ⅲ.

[16] HOLLIDAY D, ST-CYR G, WOODS N E. A radar ocean imaging model for small to moderate incidence angles[J]. International Journal of Remote Sensing, 1986, 7(12): 1809 -1834.

[17] PHILLIPS O M. The dynamics of the upper ocean(second edition)[M]. Cambridge University Press, 1977.

[18] STOLTE S. Dynamics of short waves and wave breaking[R]. (Federal Armed Forces Underwater Acoustics and Marine Geophysics Research Institute,Kiel, Germany)Report1990-4, 1990.

[19] STOFFELEN A C M, ANDERSON D L T. Scatterometer data interpretation: derivation of the transfer function CMOD4[J]. Journal of Geophysical Research, 1997, 102(C3): 5767-5780.