改进的非均匀频率采样配准双基杂波抑制方法

李迎春 李景文

(北京航空航天大学电子信息工程学院201教研室，北京 100191)

1. 引 言

双基地雷达探测范围广，抗干扰能力强，但下视模式的机载双基雷达的地杂波也非常复杂[1]，有效抑制地杂波是动目标检测的关键。空时自适应处理(STAP：Space Time Adaptive Processing)可用于双基地杂波抑制[2]，但杂波的距离依赖性带来协方差矩阵的估计损失，造成杂波抑制能力下降[3]。

经过近十年的发展，目前提出的可用于克服双基地杂波距离依赖性的方法包括：

1) 基于STAP加权矢量展开的导数更新法(DBU：Derivative Based Updating)[4]和非线性时变加权(NL-TVW：Nonlinearly Time-Varing Weighting)技术[5]。DBU和NL-TVW方法均不需要已知系统配置先验知识，但DBU使处理自由度增倍，要求的训练数据增多；NL-TVW相比DBU性能有一定的提高，但运算量进一步增加。

2) 基于双基地杂波空时快拍数据处理的方法有多普勒移位法(DW：Doppler Warping)[4]、角度多普勒补偿法(ADC：Angle-Doppler Compensation)[6]和自适应多普勒补偿法(A2DC：Adaptive Angle-Doppler Compensation)[7]。文献[8]对比这几种方法的性能，DW和ADC需要已知系统先验知识，A2DC能提高算法对系统不精确信息或错误信息的鲁棒性, 但数据处理非常复杂，且它们均只完成峰值响应补偿，对副瓣杂波抑制能力有限。文献[9]针对非正侧阵单基地雷达，提出改进的DW法，该方法理论上可用于双基地雷达，但同样无法实现副瓣匹配滤波。

3) Lapierre等[10-11]提出杂波谱的配准补偿法(RBC: Registration-Based Compensation )，所谓“谱配准”，即通过一定的补偿处理，使训练单元的杂波空时谱分布与待测单元一致，从而消除杂波的距离依赖性，RBC是对功率谱密度的处理，实施比较复杂；可实现主副瓣杂波补偿的方法还有杂波谱的非均匀频率采样配准法(RB-NFS: Registration-Based Nonuniform Frequency Sampling)[12-13]，RB-NFS是杂波数据域内的处理，操作相对简单，但要求频率采样所构造的杂波空时导向矩阵具有列满秩特性 (这里称为“保列秩”)。

考虑到RB-NFS易于操作，将其应用于机载双基地杂波抑制，针对处理中的问题提出相应的改进方案，改进后的RB-NFS不再受“保列秩”的限制，在较少的训练样本下可得到有接近最优STAP处理的性能。

2. STAP基本理论及双基地STAP

STAP通过权矢量W∈CNM×1对杂波空时快拍数据加权实现二维滤波，其中N为空间通道数，M为相干处理间隔内的脉冲数。输出信杂噪比(Signal-Clutter-Noise Ratio:SCNR)最大的权矢量可写为

Wopt=μR-1S

(1)

改善因子(IF：Improvement Factor)从整体上描述STAP处理器对杂波的抑制能力，定义为输出信杂噪比与输入信杂噪比之比。由式(1)可求得最优改善因子IF.

(2)

实际上R未知，设待检测的距离门(称为待测单元)为r，通过在待测单元附近选取若干距离门(称为训练单元或训练样本，标记为k)，利用训练单元的空时快拍数据可对R进行估计。若训练样本中存在污染(强反射动目标或杂波孤立点)，则首先需要去污[14]，由于文章侧重杂波抑制，这里假设样本均未被污染。第k个训练单元对应的空时快拍数据Xk可写为

Xk= (x1,1,…x1,M,x2,1…x2,M,

…xN,1,…xN,M)

(3)

(4)

式中，K为训练样本数。

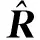
机载双基地杂波空时分布具有严重的距离依赖性[2]。角度-多普勒曲线(归一化空间频率vs.归一化多普勒频率)是杂波空时分布的重要体现，图1是三种双基地几何配置下杂波的角度-多普勒轨迹，不同的曲线对应不同的双程斜距Rs.

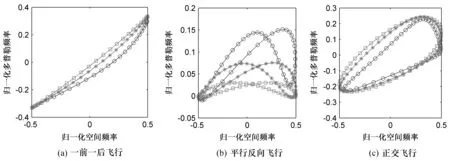
图1 角度多普勒曲线(o：Rs=20000 m；*：Rs=40000 m；：Rs=100000 m)

由图1可以看出，不同配置下曲线差异较大，即杂波空时分布受雷达几何配置影响。无论在哪种配置中，不同的斜距对应的曲线并不一致，说明杂波空时分布与距离相关，即为杂波的距离依赖性，因此，杂波不满足同分布条件，直接以式(4)估计协方差矩阵必然存在误差，使STAP性能下降。

3.机载双基地雷达RB-NFS法分析

3.1 RB-NFS法介绍

若将距离门k对应的地面区域划分成NC个小杂波元，则距离门数据Xk可表示成这些杂波元回波信号的叠加，写成矩阵形式即为

Xk=Vkgk

(5)

式中：Vk=[vk,1,vk,2,…，vk,NC]；gk=[gk,1,gk，2…gk,NC]T；vk,n和gk,n(n=1,2,…,NC)分别为杂波元空时导向矢量和幅相因子；

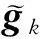
(6)

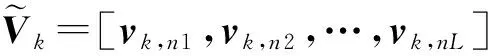
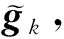
3.2 “保列秩”性

RB-NFS在机载双基地杂波抑制中的首个问题是“保列秩”性会带来的杂波空时导向矩阵Vr和Vk基列求取的复杂性，并引起杂波抑制不充分。

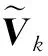
杂波抑制的有效性取决于配准的杂波谱与真实谱的逼近程度。如果配准后的谱和真实杂波谱存在偏差，加权形成的滤波器的杂波抑制凹口可能会偏离实际杂波或变浅，导致杂波抑制能力不足。如果在实际上存在杂波谱的频率点，由于配准过程中各种原因使配准后该频率处杂波能量消失，此时利用配准谱构成的滤波器在该频率处不能形成凹口，导致杂波无法抑制。两种情况可统一表述为杂波抑制不充分现象。

3.3 协方差矩阵最大似然估计

杂波抑制能力对训练样本数目的依赖，称为RB-NFS在双基地杂波抑制中的第二个问题。

第5节的仿真对此处的分析进行验证。

4.改进的RB-NFS法

4.1 “保列秩”性改进

给出两种改进方案克服“保列秩”性的限制。

4.1.1 利用Moore-Penrose广义逆

式(5)给出的距离门的空时快拍数据重写为

Xk=Vkgk

(7)

由于处于同一距离门内的杂波元数目巨大，Vk列相关，式(7)为无解式。为避免RB-NFS对Vk基列的搜索，可引入Moore-Penrose广义逆(又称M-P逆)，式(7)中gk的最佳最小二乘解可写为

(8)

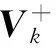
若Vk的奇异值分解式为

Vk=UDVH

(9)

(10)

4.1.2 利用对角加载技术

式(5)可改写为

(11)

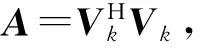
(12)

式中：I为单位阵；α为一正常数。

A为正规阵，则B也为正规阵，且特征值等于A的特征值与α之和。

对角加载操作容易，但α的选择要遵循下面原则，首先α要比较小，保证对角加载后A的对角元素改变很小，引起的杂波元频率对的变化可以忽略，同时α又不能太小，因为要保证对角加载后A为满秩阵，一般可取0.0001～0.1。可得估计幅相因子矢量

(13)

4.2 协方差矩阵求解改进

设待测距离门r内与极角φ所对应的杂波元幅相因子为gr,φ，空时导向矢量为vr,φ，杂波真实协方差矩阵可写为[15]

(14)

gr,φ可由训练单元幅相因子估计得到[12]。

(15)

由式(14)和(15)，我们可得杂波协方差矩阵新的计算公式。

(16)

只要谱配准准确，式(16)可近似认为是杂波真实协方差矩阵计算的离散形式，因此，利用式(16)代替RB-NFS中最大似然估计的协方差矩阵，可大大降低STAP杂波抑制能力对训练样本数的要求。

5. 仿真实验分析

设阵元数N=8，脉冲数M=8；脉冲多普勒频率PRF=2000 Hz，波长λ=0.3 m；发射平台速度Vt=100 m/s，高度Ht=4000 m，接收平台速度Vr=200 m/s，高度Hr=2000 m，基线长10000 m，杂噪比CNR=40 dB，距离门宽为0.667 μs。检测单元对应双程斜距为20000 km。

图2(看201页)是RB-NFS处理改善因子图，以传统SMI处理和理论最优处理(Optimum)作对比，其中图2(a)～(c)对应训练样本数K=30，图2(d)～(f)对应K=10。图中比较了三种几何配置的IF曲线。

可以看出，在K较大时，传统SMI处理具有一定的杂波抑制能力，但效果有限，若训练样本减少，如K=10，SMI基本丧失杂波抑制能力。相比最优处理，图2(a)中RB-NFS的杂波凹口深度有限；图2(b)和图2(c)两种配置下，杂波空时分布为闭合曲线(见图1(b)和图1(c))，改善因子理论上应有两个凹口，但RB-NFS只有一个凹口与最优处理基本一致，另一凹口完全消失，这正是上文分析的配准过程中谱损失，归根结底是空时导向矩阵“保列秩”性引起的，说明RB-NFS存在杂波不充分抑制。比较图2(a)～(c)和2(d)～(f)，当训练样本数减少时，RB-NFS杂波凹口变宽变浅，杂波抑制能力下降，这正是最大似然估计杂波协方差矩阵引起的。

图3(看201页)和图4(看201页)分别是M-P逆和对角加载改进后RB-NFS的某一波束下的改善因子图，杂波协方差矩阵利用文中新方法计算(式(16))，K=2.

由于训练样本很少，SMI已完全失去杂波抑制能力。三种几何配置下，两种改进后的RB-NF均不存在杂波抑制不充分现象，尽管只有两个训练样本，IF曲线与最优处理基本重合，说明处理器具有接近最优的杂波抑制能力。

仿真时发现即使是波束指向不同，两种改进后的RB-NFS的IF均与最优处理器基本一致，考虑篇幅问题，只给出某一波束的IF图，由图3和图4看到，三种几何配置下IF均与理想情况接近，说明改进方法在秩亏条件下具有较好的杂波抑制稳定性。

6. 结 论

深入分析非均匀频率配准(RB-NFS)技术在机载双基地杂波抑制中的应用，发现存在两个问题：

1) RB-NFS在杂波谱配准过程中要求杂波空时导向矩阵具有列满秩特性，这一方面增加矩阵构造的复杂性，另一方面由于矩阵基列对应的杂波元频率有限，会带来杂波谱配准过程中的损失，出现杂波抑制不充分现象；

2) RB-NFS杂波谱配准后利用最大似然估计求杂波协方差矩阵，估计精度依赖于训练样本数，要提高估计精度，运算量就要增加。

针对问题一提出两种方案，引入Moore-Penrose广义逆矩阵和采用对角加载技术，两种方案改进后的RB-NFS均不再要求杂波空时导向矩阵满足列满秩条件，避免了杂波不充分抑制现象，且导向矩阵的构造变得比较简单；针对问题二，给出新的杂波协方差矩阵计算公式，可看作真实杂波协方差矩阵计算的离散表示，避免了最大似然估计，可大大减少训练样本，从而减小运算量。仿真验证了文章对RB-NFS分析的正确性，同时证明RB-NFS改进方案的有效性，改进后的RB-NFS仅在两个训练样本即可得到近似最优的杂波抑制能力。

[1] 杨 博, 周一宇, 黄知涛. 空基运动平台照射源的无源雷达杂波建模[J]. 电波科学学报, 2009, 24(6): 1099-1103, 1178.

YANG Bo, ZHOU Yiyu, HUANG Zhitao. Modeling of the ground clutter on passive radar based on airborne illuminator [J]. Chinese Journal of Radio Science, 2009, 24(6): 1099-1103, 1178. (in Chinese)

[2] KLEMM R. Comparison between monostatic and bistatic antenna configuration for STAP[J]. IEEE Transactions on Aerospace and Electronic System, 2000, 36(2): 596-608.

[3] MELVIN W L, CALLAHAN M J. Bistatic STAP: application to airborne radar [C]// Proceedings of IEEE 2002 Radar Conf., 2002: 1-7.

[4] KOGON S, ZATMAN M. Bistatic STAP for Airborne Radar [R]. Lexington: ASAP Workshop, MIT Lincoln Laboratory, 2001.

[5] 段 锐, 汪学刚, 陈祝明, 等. 机载双基STAP非线性时变加权技术的研究[J]. 电波科学学报, 2009, 20(1): 157-162, 173.

DUAN Rui, WANG Xuegang, CHEN Zhuming, et al. The study on air-borne bistatic STAP nonlinearly time-varying weighting techniques [J]. Chinese Journal of Radio Science, 2009, 20(1): 157-162, 173. (in Chinese)

[6] HIMED B, ZHANG Y H, HAJJARI A. STAP with angle-doppler compensation for bistatic airborne radars [C]// IEEE National Radar Conf., Long Beach, California, 2002: 311-317.

[7] WILLIAM L M, HIMED B, MARK E D. Doubly adaptive bistatic clutter filtering[C]// Proc. of 2003 IEEE Radar Conference, Huntsville, AL, 2003: 171-178.

[8] 鲁远耀，马小兵. 双基雷达MTI杂波非静态特性消除方法 [J]. 测试技术学报, 2008, 22(4): 291-295.

LU Yuanyao, MA Xiaobing. Research on non-stationary clutter mitigating techniques in bistatic MTI radar [J]. Journal of Test and Measurement Technology, 2008, 22(4): 291-295. (in Chinese)

[9] 龚清勇，朱兆达.非正侧视机载雷达杂波抑制算法研究[J]. 电子与信息学报, 2009, 31(4): 977-980.

GONG Qingyong, ZHU Zhaoda. Study on clutter suppression algorithm for airborne radar with non-sidelooking arrays[J]. Journal of Electronics & Information Technology, 2009, 31(4): 977-980. (in Chinese)

[10] LAPIERRE F D, VERLY J G. Computationally-efficient range-dependence compensation method for bistatic radar STAP [C] // IEEE National Radar Conference, Arlington, VA, 2005:9-12.

[11] LAPIERRE F D, RIES P, VERLY J G. Foundation for mitigating range dependence in radar space-time adaptive processing [J]. IET Radar Sonar Navig., 2009, 3(1): 18-29.

[12] 郁文贤，张增辉，胡卫东. 基于频率非均匀采样杂波谱配准的天基雷达STAP方法[J]. 电子与信息学报, 2009, 31(2): 358-362.

YU Wenxian, ZHANG Zenghui, HU Weidong. STAP method for space based radar based on spectrum registration with non-uniformed frequency samples [J]. Journal of Electronics & Information Technology, 2009, 31(2): 358-362. (in Chinese)

[13] XIE Wenhong, WANG Yongliang. Range-dependence compensation method for bistatic STAP radar [C] // 2008 Congress on Image and Signal Processing, Sanya, Hainan, China, 2008: 503-506

[14] 宁 蔚，廖桂生.机载双通道雷达空时自适应处理中的样本去污[J].电波科学学报 2007， 22(3):470-475.

NING Wei, LIAO Guisheng. Elimination of pollutions in training samples for airborne dual-channel radar’s space-time adaptive processing [J]. Chinese Journal of Radio Science, 2007, 22(3): 470-475. (in Chinese)

[15] LAPIERRE F D. Registration-Based Range-Dependence Compensation in Airborne Bistatic Radar STAP [D]. Belgium: University of Lie’ge, Lie’ge, 2004.

[16] 王永良，彭应宁.空时自适应信号处理[M].北京：清华大学出版社，2000，1-14.