职前数学教师学科知识的调查研究——以函数为例

龚玲梅，黄兴丰，汤炳兴，田 中，杨惊雷

（常熟理工学院 数学与统计学院，江苏 常熟 215500）

一、问题的提出

教师专业化发展已成为教育界备受关注的热点。教师专业化发展的内涵在于教师教育素质的提升和发展[1]。知识作为教师教育素质的一个重要方面，是教师成为一个合格教育者的基本保证。关于教师需要什么样知识的研究，已成为近20年来迅速增长的教师教育研究的一个焦点议题[2]。尽管研究者们的结论各有不同[3-5]，但都强调了“学科知识”和“学科教学知识”在教师知识中的重要地位。其中丰富的“学科知识”是个体成为一个好教师的必要条件。

与新手相比，专家教师的一个明显特征在于拥有大量的本领域的知识，以及知识的高度组织化与结构化[6]。而对于即将成为教师的职前教师，他们的学科知识的情况如何？本研究即考察他们学科知识的特点，为职前教师课程设置、培养方式提供参考。

二、研究方法

（一）被试的选取

本研究选取的职前教师来自苏州的一所本科院校，共101人，其中49人是大学三年级（下）学生，52人是大学四年级学生。所有被试所学的专业是数学教育，而且都已经修完了大学本科阶段的主要课程。

（二）研究工具

数学学科知识包含的内容很广，而函数知识既是中学数学的重要组成部分，又是高等数学的核心内容，与其他知识存在密切联系。从函数知识入手，更能考察高等数学的学习对职前教师学科知识的影响。

Even[7，8]认为函数知识应当涉及下列7个方面：（1）函数的本质特征，（2）函数的不同表征，（3）函数图像性质，（4）复合函数和反函数；（5）高中课程的初等函数；（6）关于函数的理解；（7）关于数学的知识。在这7个方面中，前5项是本研究中所指的学科知识，后2项是关于学科知识其他方面的知识。

本研究参照Even关于函数知识的前5项，又由我校组织的数学教学研讨班中部分初、高中数学骨干教师的多次研讨，提出函数知识的假设模型，编制测试问卷，并随机抽取56名数学师范方向的大三学生进行预测试，根据测试情况反复斟酌修改，确定3组24个问题形成标准化测试问卷。这3组问题分别是A：概念表征；B：图像性质；C：反函数和复合函数。每组有2类构成，每类共4个问题，详见表1。

24个问题都设计为选择题。选择题分2类：第1类，只有一个正确答案，选对得1分，否则0分；第2类，有多个正确选项，全选对得1分，选对超过半数的得0.75分，选对一半0.5分，少于半数0.25分，全错0分。测试问卷3组的Cronbach内在一致性α系数分别为：0.514、0.554和0.552，显示了较好的可信度。

（三）研究的实施

测试在学校教室进行，一人一桌并有教师监考，时间不限，但大部分职前教师在1个小时左右完成测试。结合测试问卷的有关问题，对部分职前教师进行了访谈。最后用Excel和SPSS统计软件对调查数据进行统计处理与分析。

三、数据整理和统计分析

（一）职前教师函数知识总体分析

职前教师在测试问卷上总得分频数分布见表2，在函数知识3个成份6个子类及总体得分见表3。其中得分率这一指标是测查对象在某类知识上的平均得分除以该类知识的总分，用它容易比较测查对象在各类知识上的表现。CV系数是测查对象在某类知识上的标准差与其平均数的百分比。它既能比较不同单位资料的差异程度，又能比较单位相同而平均数相差较大的资料的差异程度。

统计数据显示职前教师测试问卷总得分率为70.42%，总平均分16.90分，有59.41%的职前教师总得分在16分至20分之间。在函数知识的3个成份A、B、C上得分率依次是64.38%、79.75%和67.13%，即表现较好的是B（图像性质），其次是C（反函数和复合函数），A（概念表征）相对较差些。在函数知识的3个成份上的CV系数从低到高依次为B、C、A，这表明在B上的得分比较整齐，A上的离散程度较大。统计数据还表明在函数知识的6个子类中得分率较低的是A2不同表征和C1反函数，分别仅为54.00%和58.25%，且CV系数也都较大，说明职前教师对这两类知识的掌握不够理想，且分化较大。除A2、C1外，在子类A1上的表现高低不齐，尽管在这类上得分较好。

（二）职前教师函数知识各成份具体分析

（1）职前教师在函数概念表征上的表现：测试卷1至8题是考查职前教师对函数概念的理解，其中1至4题是关于函数概念本质，5至8题是关于函数不同表征及相互之间的转换。各题的得分率见图1，在A成份及两个子类A1和A2上的表现见表3，且由表4可知，他们在A1和A2上表现出显著差异(P＜.001)。

职前教师在函数概念理解上的主要问题有：①对函数的值域与陪域概念不理解。有11.88%的职前教师认为函数是从定义域到值域的函数，而不能说是从定义域到其陪域的函数。②认为函数的图像一定是连续不断的光滑曲线。第3题给出了一条不连续的曲线，问是否表示定义域上的一个函数，有11人选A，9人选D，即有19.80%的人犯此类错误。③函数概念中对应法则表示的多样性对理解概念有较大影响。职前教师对第4题中的“数列{an}的通项an是n的函数”和“组合数是的函数”这两种表述都有39.60%的人认为是不对的，只有16人认为“SΔABC表示ΔABC的面积，CΔABC表示ΔABC的周长，那么SΔABC是CΔABC的函数”是错的，即这一问的正确率仅为15.84%。④对函数与方程之间的关系理解不清。职前教师在第5题上表现充分证明了这点。第5题是对两句话“能用方程表示的关系是函数”和“任何函数总可以写成方程的形式”做出正确与否的判断，本题的得分率仅为52.48%。⑤对函数概念不同表征之间的转换发生困难。函数概念表征具有多样性的特点，一方面表现在定义域、值域表示的多样性，可以用集合、区间、不等式等不同形式表示；另一方面表现在表示方法的多样性，可以用图像、表格、对应、解析式等，从每一种表示中都可以独立地抽象出函数概念来。第6题需要将二次多项式、方程及函数的图像表征等结合起来考虑，第7题是将函数的表格表示转换为其他表示形式，分别有36.63%和33.66%的职前教师回答错误。第8题考查的是对抽象函数的认识，需要尽可能地联系其他表征，它是24个问题中得分率倒数第二的一个，仅为34.65%。

表1 函数知识假设模型的成分

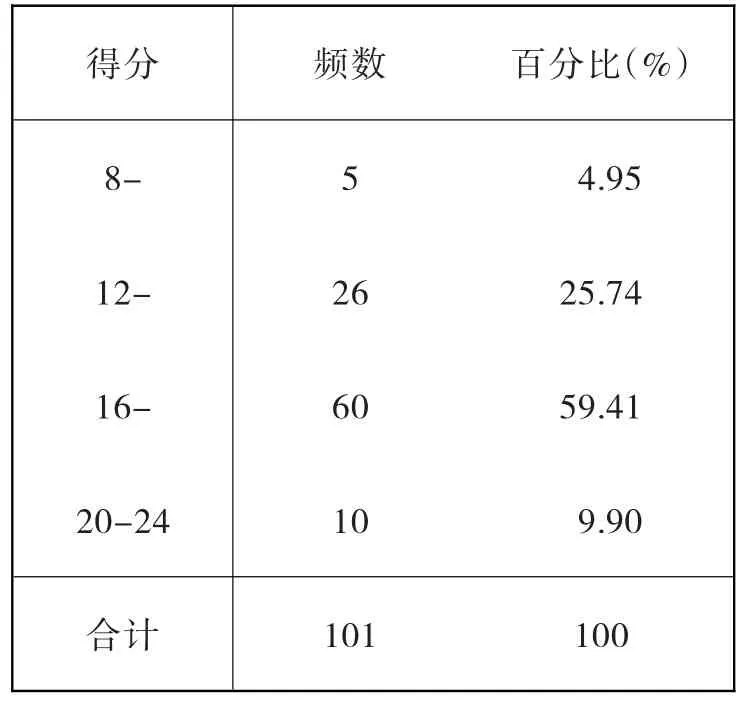
表2 职前教师测试总得分的分布

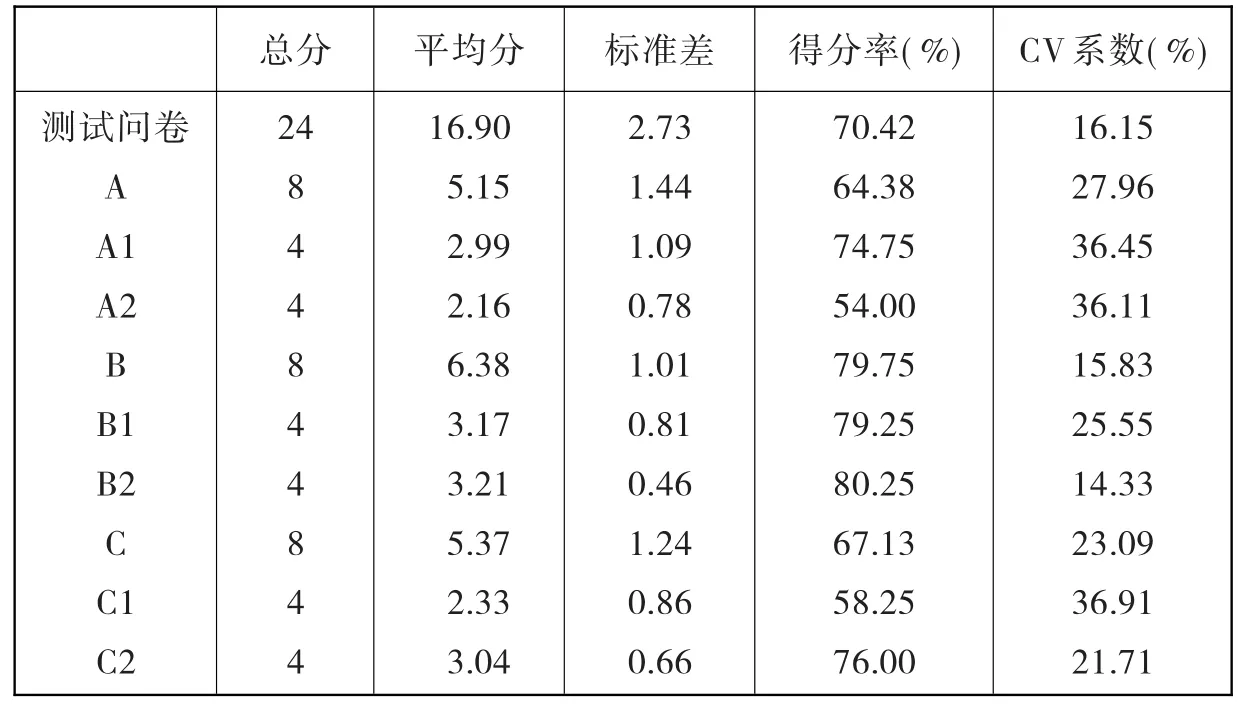
表3 职前教师在函数知识各维度上的得分情况

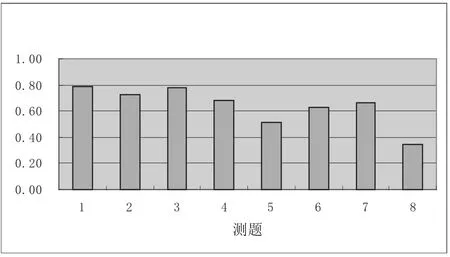
图1 职前教师概念表征8题的平均得分

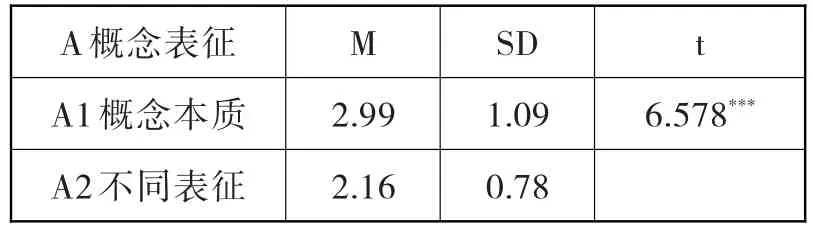
表4 职前教师概念表征的显著性检验

（2）职前教师在函数图像性质上的表现。测试卷9至16题是考查对函数图像性质的掌握情况，其中9至12题是结合一些具体的实际问题研究已给出的图像，从中获取信息，形成用函数观点处理实际问题的意识。13至16题是给出函数的表达式研究其图像的性质，形成对函数概念的整体性认识。得分率见图2，在B成份及两个子类B1和B2上的表现见表4，且由表4可知，在B1和B2上的表现没有显著差异。

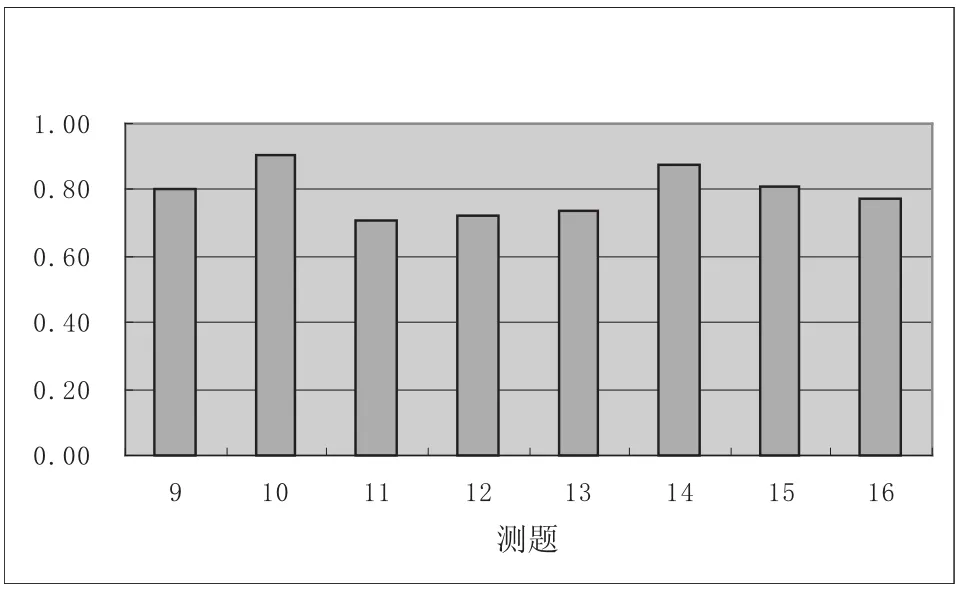
图2 职前教师图像性质8题的平均得分

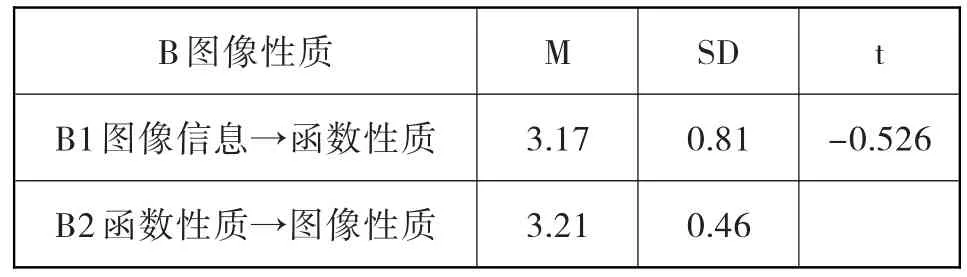
表4 职前教师图像性质的显著性检验

尽管职前教师在B成份上的表现是最好的，但还是存在不少问题。主要有：①图像所在直角坐标系中，不注意横轴和纵轴的名称。9和10题都是路程问题，横轴都表示时间，但纵轴一个表示路程，另一个表示速度。在第10题的Ⅱ上有23人答错，占22.77%。经访谈，他们出错的理由大多是看错坐标轴的单位。②在“时间—路程”坐标系中，不清楚快慢与曲线的斜率有关。第9题的Ⅱ、Ⅳ，11和12题都涉及这点，出错的分别有8人、20人、30人和29人。③正确作出具体函数图像有困难。14、15和16题给出了函数的具体表达式，但不易立即得到图像，必须通过奇偶性和单调性的判定、渐近线的确定等细节，运用一阶导数、二阶导数和极限等方法才能获得正确图像信息。这3题的第一问都是图像关于原点是否对称，回答错误的分别有15人、3人和19人。经访谈，他们会判断函数的奇偶性，但不清楚图像关于什么对称。15和16题的第二问都是指出图像的渐近线，回答错误的分别有31人和19人。14题的Ⅲ、15题的Ⅳ和16题的Ⅳ都是判定区间上的单调性，回答错误的分别有14人、28人和42人。④对于抽象函数图像的认识存在更大困难。13题是著名的狄利克雷函数，没有解析表达式，有图像但作不出，也没有实际背景。认识这一函数首先要弄清有理数和无理数的性质及在实数轴上的分布，对这题的4问回答都正确的只有29人。

（3）职前教师在反函数和复合函数上的表现。测试卷17至24题是考查对反函数和复合函数的认识，其中17至20题是关于反函数的研究，涉及反函数的定义、反函数存在的条件及反函数的性质等。21至24题是关于函数复合的研究，涉及复合函数的定义域、复合函数的条件和复合函数的值等。得分率见图3，在C成份及两个子类C1和C2上的表现见表5，由表5可知，在C1和C2上表现出显著的差异(P＜.001)。

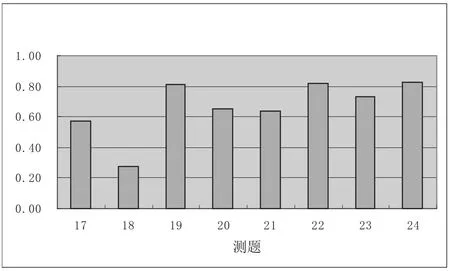
图3 职前教师复合函数与反函数8题的平均得分

职前教师在反函数和复合函数上的主要问题有：①对反函数的定义理解不透，不清楚函数在何种条件下具有反函数。只有40位职前教师认为“g(x)=x2+2x+1的反函数是”是错误的。18题是“若函数f(x)存在反函数，则关于方程f(x)=c(为常数)的根”的个数问题，回答正确的只有29人，占28.71%，本题也是24题中得分率最低的一题。②反函数与其原函数的基本数形联系不清。职前教师在19、20两题上的表现说明了这点，19题是“设y=f-1(x)是函数f(x)=2x+lnx的反函数，那么f-1(2)等于多少”，有19人没有给出正确值。20题的4问全部答对的只有49人，通过访谈，其中很多人还是通过特例得到结论。③复合函数的定义域问题。有39人认为“如果函数f(2x)的定义域是[1，3]，则f(x)的定义域是[2，6]”是不对的，有69人认为“如果函数的定义域是[1，3]，则f(x)的定义域是[1，3]”没有错。④分段函数能够复合的条件不太清楚。22题的Ⅳ中f(x)是一个分段函数，g(x)=2x，问能否复合成f[g(x)]，39人没有给出正确答案。

四、结果与讨论

（一）结果

职前教师对函数概念的理解相对最差，且呈多样性和片面性的特点。Vinner提出：“获得概念就是形成概念表象，用心学习定义不保证理解。在进行关于某个概念的一些推理时，定义并不是最活跃的因素。甚至可以被忽略掉。”本调查也印证了这点。在判断一个对象是否为函数时，有人依据定义，有人依据函数概念在头脑中的表象，概念表象与头脑中的概念名称和相关表征相联系，如概念的任何一种表示——图片、符号形式、图表、图像等。所以有职前教师将函数与方程等同，有认为函数一定可以用解析式表示、函数的图像一定是连续不断的光滑曲线等。

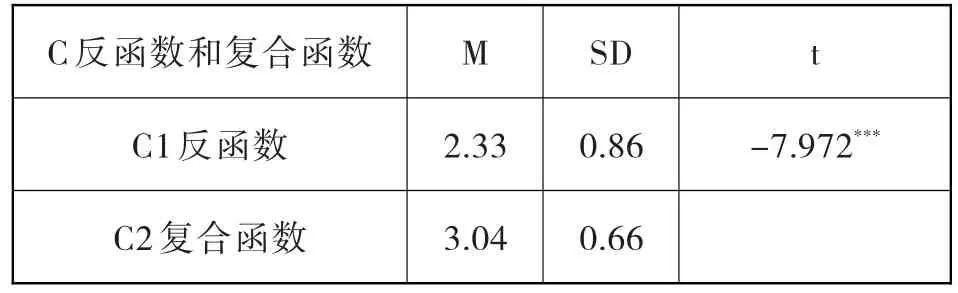
表4 职前教师反函数和复合函数的显著性检验

职前教师对函数图像性质的掌握相对最好，且在捕取图像所传递的特征信息处理现实生活问题与研究函数图像形成对函数整体性认识这两方面无显著差异，但前者的分化程度大于后者。在现实生活中，函数图像是作为刻画和描述两个变量之间的函数关系的一种重要方法。它以直观的数学语言传递着丰富的信息，职前教师在从函数图像传递的丰富信息中接收、转化及合理应用上还存在不少问题。

职前教师在反函数和复合函数的表现上差异显著，对复合函数的认识优于对反函数的认识。对反函数和复合函数的研究是对函数概念和函数性质在认识上的深化和提高。调查表明，职前教师处理反函数和复合函数的问题不很熟悉，这也从另一角度说明他们对函数概念的理解水平不高。

综上所述，职前教师在学科知识领域中所处的位置高度比我们预计的要低，而且他们学科知识的结构比较松散，缺乏相互联系。

（二）讨论

（1）职前教师培养的课程要更有利于促进对中学数学的理解。大三大四的学生学了那么多的数学专业课程，为什么对中学数学的指导作用并没有达到我们预期的效果？事实上，在大学数学专业课程里，除微积分外，多数课程与中学数学在研究对象和研究方法两方面都有着很大的不同，它们不是一种螺旋式的深入，而是一种阶梯式的跨越。这就使得大学数学专业的多数课程表面上与中学数学严重脱节。那么，职前教师的培养课程如何更有利于促进对中学数学的理解呢？一是关注基础教育的课程标准，以大学数学课程的学习内容为依托，延伸覆盖课标课程的相应内容，帮助职前教师体会大学数学课程的“临下”功能。二是重视数学教学专题学习以提升学科知识。这种学习方法直接针对中小学数学教学内容和使用这种内容知识的教学环境，能把握整个数学发展的脉络、过程以及蕴含的学科思想方法，并能运用知识的整体观高屋建瓴地反思数学或教学内容。

（2）职前教师培养方式要更有利于学科知识结构、思维结构的正向迁移。本调查以函数为例，内容与大学微积分联系密切，很多问题用高等数学的知识易解，如第9题的Ⅱ和Ⅳ、11题、12题、14题、15题的Ⅳ、16题的Ⅳ等，若能将快慢、变化率、曲线切线的斜率以及单调区间等与导数联系起来则非常容易，又如作函数的图像、反函数和复合函数，大学数学里专门有详细讲述，13题是狄利克雷函数，在讲极限、连续、可导等概念时常作为反例。调查表明，职前教师知识结构、思维结构在迁移过程中常会出现知识性、技术性的偏差。数学有效教学的重要指标是学生的数学学习能否从一个问题迁移到另一个问题，从一个情境迁移到另一个情境，从学校课堂迁移到社会生活中[9]。因此，在职前教师培养过程中，教师要考虑并运用学习迁移的规律，创设意义建构的情境，选择适宜的教学方式方法，恰当地形成和完善学生的认知结构，充分发挥正迁移的促进作用，提高教学成效。

［1］教育部师范教育司.教师专业化的理论与实践［M］.北京：人民教育出版社，2003：23.

［2］范良火.教师教学知识发展研究［M］.上海：华东师范大学出版社，2003：14.

［3］Shulman L S.Knowledge and teaching foundations of the new reform［J］.Harvard Educational Review,1997,57：1-22.

［4］Cochran K F,DeRuiter J A,King R A.Pedagogical content knowing:an integrative model for teacher preparation［J］.Journal of Teacher Education,1993,44(4)：263-272.

［5］申继亮，辛涛.论教师素质的构成［J］.中小学管理，1996，11：4-7，

［6］Chi M T H,Glaser R,Farr M.The nature of e x pertise［M］.Hillsdale,NJ：Erlbaum,1988.

［7］Even R.Subject matter knowledge for teaching and the case of functions［J］.Educational Studies in Mathematics,1990,21（6）：521-544.

［8］Even R.Subject-matter knowledge and pedagogical content knowledge:Prospective secondary teachers and the function concept［J］.Journal for Research in Mathematics Education,1993,24（2）：94-116.

［9］涂荣豹.数学学习与数学迁移［J］.数学教育学报，2006，15（4）：1-4.