大轴重货车车轮热负荷下疲劳强度分析*

侯 耐,李 芾

(西南交通大学 机车车辆工程系,四川成都610031)

铁路运输以其运量大、快速、安全、低耗能及环保等特点,已成为世界当今和未来主要发展的运输模式。随着我国国民经济的快速发展,对铁路的运输能力要求也越来越高。增大货车轴重、实现重载运输、提高货车运行速度是提高铁路运输能力、解决运能不足的有效途径。近年来,我国的通用货车轴重已由21 t提高到23 t,运煤专用车提高到25 t,为解决铁路货运能力不足的矛盾发挥了重要作用,取得了较好的经济效益和社会效益。为进一步提高铁路运能,增加货车的承载能力,提高车辆的轴重将势在必行。为此,国内相关部门目前正在研究将通用货车的轴重提高到25 t、运煤专用车的轴重提高到32.5 t的可行性。

车轮是机车车辆中走行部的部件之一,其性能直接影响车辆轴重的提高,车轮的可靠与否关系到整列车的运行安全。目前,货车的制动方式仍然是踏面制动,随着列车速度的提高和轴重的增加,列车的动能将急剧增大,由车轮踏面和闸瓦之间的机械摩擦而产生的热量也会大大增加。其结果将导致车轮热负荷的增加,对车轮的强度及疲劳寿命带来直接影响。

在长大坡道上制动,由于热量长时间输入,在辐板区域将产生高应力,此工况较常用制动和紧急制动工作条件更为恶劣。因此,以坡道制动下32.5 t轴重、制动初速为80 km/h的车轮为研究对象,对车轮辐板区域进行疲劳评定,以验证大轴重车轮的疲劳强度是否满足要求。

1 计算模型

根据国内现有的技术规范和相关技术条件,32.5 t轴重货车车轮的轮径拟定为915 mm,车轮材料为CL60,材料的性能参数除弹性模量E、比热容C、热膨胀系数α及屈服极限σs随温度变化外,其他参数基本不变。

考虑到车轮结构和热载荷的对称性,取车轮的1/2结构进行分析,其有限元模型如图1所示,其由37 466个节点和41 128个单元组成。温度场计算采用Solid70热分析单元进行网格划分,该单元每个节点只有节点温度一个自由度。当进行应力场计算时,该单元转换为与之相对应的结构单元Solid45。

图1 车轮有限元模型

2 计算载荷工况

按照UIC 510-5—2003标准,选取以下3个载荷工况:

(1)直线运行坡道制动工况:垂直动载荷P1+过盈量Δ+角速度+最高温度载荷。

(2)曲线运行坡道制动工况:垂直动载荷P2+横向动载荷H2+过盈量Δ+角速度+最高温度载荷。

(3)道岔通过坡道制动工况:垂直动载荷P3+横向动载荷H3+过盈量Δ+角速度+最高温度载荷。

2.1 机械载荷的确定

式中P0为轮重。取过盈量 Δ为0.3 mm。

在不同的载荷工况下,作用于轮轨作用点的载荷对车轮作用力的方向和位置如图2所示。

图2 机械载荷的位置和方向

2.2 热负荷确定的边界条件

采用能量转换法,列车的动能通过闸瓦与车轮踏面的摩擦转变成热能。以SS4B型电力机车双机牵引10 000 t的货物列车,制动时间30 min,冷却5 min为计算基础,列车所需总的制动力为:

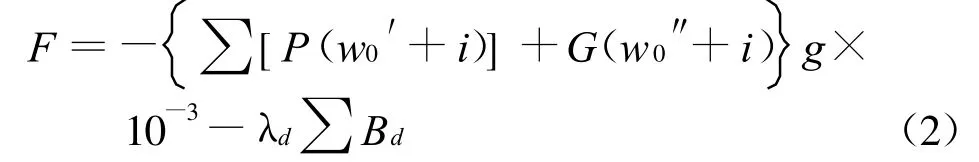
机车和车辆的基本阻力分别按式(3)—(4):

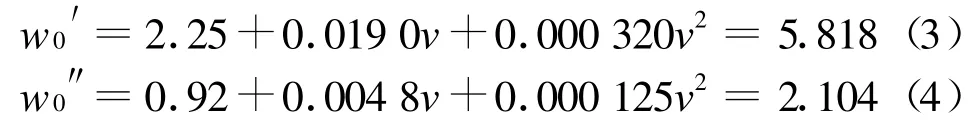
i为下坡道的加算坡度千分数,取-9‰。

则热流密度为:

式中v为车辆运行速度,m/s;n为机车与车辆的总轴数;Sf为车轮旋转一周闸瓦在踏面上扫过的面积,m2。

计算对流换热系数采用:

式中L为固体表面尺寸,m;λ为流体导热系数,W/(m◦K);Nu为谢努尔特数。

其中,Pr为普朗特数,Pr=0.687;Re为雷诺数。

u∞为空气流动速度,m/s;υ为空气的运动黏度=2.429×105,m2/s。辐射系数取值为0.66。

3 疲劳强度评定方法

车轮在计算载荷工况作用下,其应力状态为三向应力状态,而结构产生疲劳裂纹的方向与最大主应力方向相互垂直,由此按下面的方法将多轴应力转化为单轴应力:

(1)确定结构在不同载荷工况作用下的主应力值和方向。

(2)将所有载荷工况作用下结构的最大主应力方向确定为基本应力分布方向,其值为最大计算主应力σmax,计算其与结构基准线的夹角α。

(3)将在其他载荷工况作用下的主应力投影到基本应力分布方向上,其投影值最小的应力值确定为σmin,如图3所示。

(4)由最大和最小主应力值计算平均应力σm和应力幅 σa。

(5)用修正的Goodman疲劳曲线评定结构的疲劳强度。

图3 最大、最小计算主应力

4 计算结果分析

施加热负荷边界条件后,计算车轮的温度场,得到车轮踏面的最高温度随时间的变化曲线如图4所示。从图4中可以看到:车轮踏面温度随制动时间的进行而增大,在制动结束时刻温度达到峰值195.79℃。在冷却阶段,热流输入为零,车轮最高温度下降并逐渐向辐板区域转移。

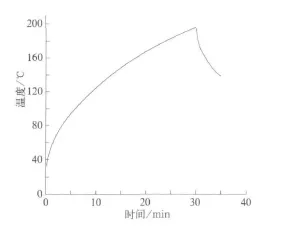
图4 车轮最高温度曲线

采用间接耦合法,将车轮在制动过程中得到的瞬态温度场作为温度载荷施加到单元转换后的车轮模型上,采用命令流的方式,将热分析结果中的节点温度值读入到结构分析中进行热应力计算。车轮辐板区域的最大von_Mises热应力随时间的变化曲线如图5所示。从图5中可以看到:车轮辐板区域的最大von_Mises热应力的变化趋势同温度走势基本一致,在温度达到最大值时也相应达到最大,即制动结束时刻达到最大值200.109 MPa,出现在临近轮毂外圆角处。图中出现的两个小波动处,即是随着制动的进行,最大von_Mises热应力出现在辐板的不同区域。

在曲线运行工况中,只施加机械载荷的情况下,辐板区的最大von_Mises应力为196.158 MPa,而联合施加机械载荷和热载荷的情况下,辐板区的最大von_Mises应力为235.112 MPa,见图6,均出现在临近轮辋的外侧。

图5 车轮辐板最大von_Mises热应力曲线

按上述给出的疲劳强度评定方法对3个载荷工况的计算结果进行处理,通过Fortran程序处理节点应力值,计算得出平均应力和应力幅,进而得到Haigh形式的修正Goodman曲线如图7所示。由图可见,车轮辐板区域很多节点的应力幅裕量不大,甚至辐板与轮毂过渡圆角区域的某些节点的应力均值和应力幅已经超出Haigh-Goodman疲劳曲线图的界限,这些节点的疲劳强度已不满足要求。若要保持车轮轴重的基础上,提高结构的疲劳强度,则应该选择合理的车轮材料,优化辐板结构。

图6 车轮辐板最大von_Mises应力云图

图7 车轮辐板区域节点Haigh-Goodman曲线

5 结论

通过仿真长大坡道制动下32.5 t重载货车车轮在热负荷和机械载荷的共同作用,对大轴重车轮危险位置的疲劳强度进行分析。分析结果表明:在制动热负荷单独作用下,车轮踏面温度随制动过程的进行而逐渐增高,并在制动结束时刻达到峰值,同时von_Mises热应力在辐板与轮箍过渡外圆角处达到峰值。辐板是结构的危险区域,在热—机耦合载荷的联合作用下,辐板在曲线运行工况中von_Mises应力最大,且出现在临近轮辋的外侧。在3个载荷工况的计算载荷作用下,对辐板区域进行疲劳强度校核。

[1] 米彩盈.铁路机车车辆结构强度[M].成都:西南交通大学出版社,2007.

[2] 刘俊红.重载货车踏面制动热响应分析研究[D].成都:西南交通大学,2006.

[3] Kncene B C H,et al.Temperature Field,deformation and Stress of Whole Wrought Wheel Under Different Braking Condition[J].Foreign Rolling Stock,1996,(4):17-20.

[4] L.Rmanan,R.Krishna Kumar,R.Sriraman.Thermomechanical finite element analysis of a rail wheel[J].International Journal of mechanical Sciences,1999,(41):487-505.

[5] 徐传来,米彩盈,李 芾.基于轴对称模型的货车车轮结构疲劳强度分析[J].交通运输工程学报,2008,8(6):20-23.

[6] 郑红霞,谢基龙,周素霞,等.基于有限元仿真车轮多轴疲劳强度分析[J].北京交通大学学报,2009,33(4):54-59.

[7] 刘会英,王 农.提速货车车轮热负荷试验研究[J].铁道车辆,2000,38(4):15-19.