线性规划中几种内点算法的比较

福州工业学校 林育山



线性规划中几种内点算法的比较

福州工业学校 林育山

该文是关于内点算法的一篇综述，对几种较为实用的求解线性规划问题的算法进行总结，包括单纯形法、椭球算法、Karmarkar算法、原仿射尺度算法等，并对这些算法进行比较。

线性规划 内点算法 比较

1 问题的提出

1947年，美国数学家G.B . Dantzig提出了求解线性规划问题的通用方法——单纯形法，大量的实际应用表明，单纯形法是一种行之有效的解线性规划问题的算法。但是在理论上，单纯形法并不是一个“好算法”，特别是在1972年美国学者V.Klee与G.L.Minty发表了一个例子，通过构造一个病态的线性规划，说明了单纯形法在解决某些极端的例子中效果不好，很多研究线性规划的数学家开始探讨解线性规划的NP问题。1979年，前苏联数学家哈奇扬发表了椭球算法，并证明了该算法是个多项式时间算法，说明线性规划的多项式时间算法是存在的，但在实际应用中，这一算法并没有很强的实用性。1984年，在美国贝尔实验室工作的印度籍数学家N.Karmarkar提出了解线性规划的投影尺度法，这也是一个多项式时间算法，它比椭球法优化了很多，这一工作一时引起了很多数学家对内点算法的研究热情，在不断的改进中，一些新的、改进的或变形的内点算法相继出现。无论是内点算法还是椭球算法，它们有一个共同点，就是采用了非线性规划的一些思想来解决线性规划问题。

2 几种算法的简单介绍

2.1 单纯形法

将线性规划问题（LP）写成如下的矩阵形式：

设是的一个基，不失一般性的，设它由中的前列所组成，由高等代数的知识，必可将矩阵（1）通过初等变换变为如下形式：

（3）式可以写成矩阵的形式如下：

注：

单纯形法的具体步骤如下：

Step1 列出初始表，在表中找到一个初始基，化为标准形，得到对应初始基的基本可行解。

Step2 检查标准形表上的检验数(c=m+1, 是否均为正数，若是，则停止，当前的基本可行解为最优解，否则，进入Step 3。

在前面单纯形法的介绍中，我们强调了一个非退化的前提，在退化的情况下，用上面的步骤去迭代时，可能出现死循环，对于这个问题，先后有Charnes提出了摄动法，Dantzig、Orden、Wolfe提出了字典序法以及Bland提出了Bland法则，本论文中我们仅介绍Bland法则。

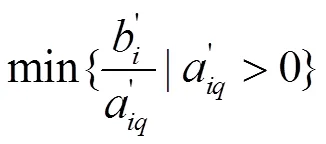
2.2 椭球算法

如果能够找到求解严格不等式组多项式时间算法，那么就有（LP）问题的多项式时间算法。椭球算法就是一种通过寻求严格不等式组的多项式时间算法，来证明线性规划问题有多项式时间算法。可以理解为把线性规划问题转化为（8）的形式，即为弱不等式组，然后求出相应的严格不等式组的解，从而导出弱不等式组的解，则可以求出原线性规划问题的最优解。所以椭球算法的本质是求严格不等式组的解。下面简单介绍一下椭球算法的原理。

2.2.1基本定义

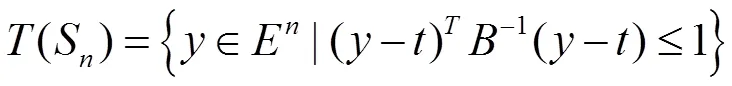
2.2.2椭球算法

2.3 Karmarkar算法

Karmarkar算法运用了求解非线性规划问题的思想来解决线性规划问题。这种算法是在把一般线性规划问题转化为Karmarkar所特有的标准型，再利用一种求解这种标准型的算法最终求出最优解。Karmarkar算法把线性规划问题转化成它所要求的那种标准型，我们称之为Karmarkar标准型，形式如下：

其中这个标准型还要求满足以下三个条件：

Karmarkar算法的具体步骤：

下面对Karmarkar算法从一个迭代点寻求下一个迭代点的原理进行解释。

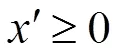
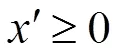
注:

2.4 原仿射尺度算法

原仿射问题与上面介绍的两种内点算法不同，它是可以求解标准形式的线性规划问题LP：

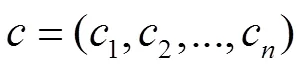
不失一般性的，设秩()=，并设

原仿射尺度算法与Karmarkar算法在构造原理上有很多的相似之处，它的好处是不用把一般的线性规划问题转化为Karmarkar标准型，由于把一般的问题转化为Karmarkar标准型并不容易，所以原仿射尺度算法在实际应用中是很受推崇的。但是原仿射尺度算法在理论上并未被证明是一个多项式时间算法。

3 几种算法的比较

名称解决的问题解决原理算法的时间应用价值和优缺点 单纯形法直接解决线性规划问题 s.t 在基本可行解中寻找最优基本可行解指数形时间算法大量的实际应用证明单纯形法是一种行之有效的解线性规划问题的算法，但对于一些极端的问题，单纯形法效果不好 椭球算法把解决线性规划问题转化为求解严格不等式组通过不断缩小严格不等式组的解所在的椭球的体积，最终确定是否有解多项式时间算法椭球算法证明了求解线性规划问题的多项式时间算法的存在，但在实际应用中，远没有单纯形法好用 Karmarkar算法把解决线性规划问题转化求解Karmarkar标准型的问题从可行解的多面体内部一个点出发，产生一个直接穿过多面体内部的点列，从而得到所需的最优解多项式时间算法是一种行之有效的多项式时间算法，但把一般的线性规划问题转化为Karmarkar标准型并不容易 原仿射尺度算法可以直接求解线性规划问题在寻找迭代点的原理上与Karmarkar算法原理相似，但在确定何时停止迭代运用了线性规划的对偶理论在理论上还未被证明是多项式时间算法实际效果优于Karmarkar算法，在中大规模的线性规划问题上，它们的求解效率优于单纯形法

[1] 张建中，许绍吉. 线性规划[M]. 北京: 科学出版社，1990.

[2] 姚恩瑜，何 勇，陈仕平. 数学规划和组合优化[M]. 杭州: 浙江大学出版社，2001.

[3] Papadimitriou H C，Steiglizt K.，Combinatorial optimization algorithms and complexity[J]. Printice-Hall,1982.

[4] P.GaCs and L.Lovasz. Khachian’s algorithm for linear programming[J]. Math,Programming Study 14 (1981): 61-68.