用结构矩阵优化教学计划进程

周苏闽

(淮阴工学院生命科学与化学工程学院，江苏淮安223003)

0 引言

高等学校教学计划进程安排的目的，是在合适的时间、以适当的方式将教学内容传授给学生。教学计划的安排是一个牵涉内容相当广泛的系统工程，以往制订教学计划时，一般采用的方式多为相互借鉴法，或依据编制者的经验来进行安排。前者需花费大量的人力物力进行调研，而后者对编制者的水平和经验要求很高，教学计划安排的合理与否与编制者的水平关系很大。

无论是参照其它院校的教学计划还是依靠编制者的经验，或多或少都带有一定的盲目性，反映在教学计划安排上因人而异。随着科学技术的迅猛发展，学科间的交叉、渗透越来越多，一大批新兴学科、边缘学科不断涌现，使得课程体系的更新加快、复杂性也越来越高。采用上述方法编制教学计划周期长，科学性差，不符合时代的要求。为此，本研究采用建立数学模型的方法，通过对数学模型的优化，制订教学计划。这一方法通过对课程体系及课程内容的相关性分析，应用结构矩阵理论建立起数学模型，采用数学方法对数学模型进行分析、解耦，最终确定教学计划安排的参考方案。这不仅使得教学计划安排更具科学性，而且加快了教学计划进度安排的速度。根据这一理论编制而成的计算机程序，可以在对课程体系深入分析的基础上，迅速生成较为科学的教学计划。

1 数学模型的建立

1.1 教学计划进程分析

在高等学校教学中，每个专业一般都会涉及到25～35门课程，这些课程的内容涵盖很广，关系也比较复杂。有的是自成体系;有的具有相对的延续性(即一门课程需要另一门课程的内容作为先导知识);也有的相互之间存在着相关性(即课程内容之间存在着相互依赖关系)，形成一种紧密的耦合关系，这种耦合关系有时甚至会涉及到很多课程(见图1)。因而在教学计划安排过程中，应合理地安排有关课程的顺序，使课程间不至于冲突。但这并不是一件容易的事，特别是当许多课程都相互耦合时，往往会出现捉襟见肘、难以兼顾的情形。因而必须采取一定的措施，来解消这些冲突，结构矩阵的方法正是在这种情况下提出的。

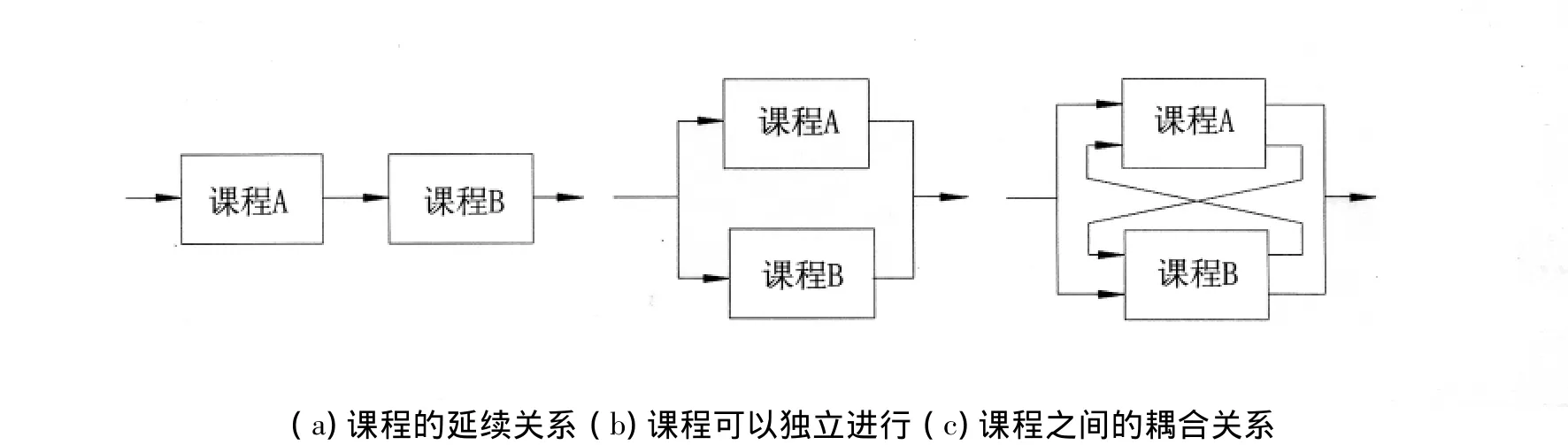
图1 课程之间的几种关系

1.2 结构矩阵方法的原理

结构矩阵方法是一种目前应用于工程任务管理的有效方法，其基本原理是将“任务”按相关性列成一个二进制数值矩阵，然后对矩阵分析，找出任务过程安排的最优解。其方法简要说明如下:如果有一个5个任务的“工程”，分别用A～E列成任务相关性表，见表1。

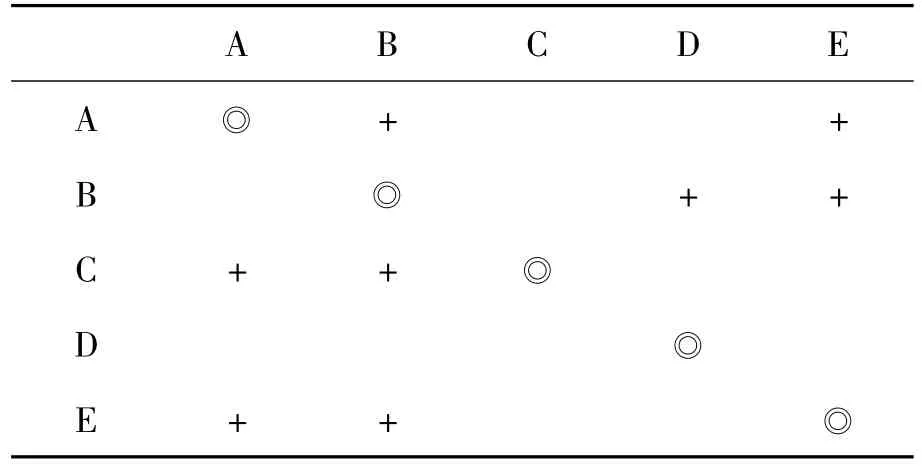
表1 任务相关性表

在其行列相交处，表明它们之间的关系，如果两个工程具有相互依赖性，则在其交叉位置记以符号“+”来表示。如:在A行B列处的“+”号，表示完成A任务必须由B任务提供信息反馈，亦即任务B为任务A的先决条件，依次类推。

将表1写成矩阵形式，把其中的“+”号用数值1代替，其它地方补以零，这样就构成了一个二进制矩阵，工程上称这个矩阵为设计结构矩阵(Design Structure Matrix)，简称DSM。本文仍延用这个名词，简称为“结构矩阵”。

由相关任务表构成的矩阵称“原始设计结构矩阵”(Original DSM)，见图2(a)。

即:D=［aij］

在这个矩阵中:

如果aij=1则表明在执行任务i时，需要任务j提供信息。

而aij=0则表明任务i和任务j不相关。

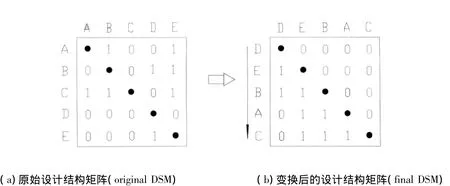
图2 设计结构矩阵及其变换结果

对该矩阵进行一系列行列变换(第一类初等 变换)，把它变换成一个下三角阵，见图2(b)。

进行这样的变换后，按图中箭头方向表达的排序DEBAC，排在前面的工程如D，与排在后面的工程如E、B等均无依赖性，表现为该行的EBAC位置元素都为0，同样E行元素同样也只与排在其前面的任务D相关，与后面的元素BAC无关。

如果按D－E－B－A－C安排工程任务，在执行前面的任务时，与后面的任务因为没有相关性(矩阵的上三角区均为0)，故不会影响任务执行过程。而排在后面的任务，因为有了前面已经完成了的任务提供足够的信息，可顺利执行，任务就能合理地安排。

值得注意的是，当矩阵中的元素不断增加，会使原始设计结构矩阵的复杂程度不断提高，这时设计结构矩阵就可能无法变换成标准的下三角阵，解决这一问题的方法是把它转换成块下三角阵，见图3。

通过矩阵分块法，把有紧密耦合关系的任务组合在一个矩阵块中(如图3矩阵的EFGH和JKL两个矩阵块)。这样只有同一矩阵块内任务之间有紧密耦合关系，而块与块之间没有相互的耦合关系。执行时只要将同一子块中的任务组当成一个任务，构成一个多功能小组来完成这一任务。参照工程任务管理的方法，把每一门课程看成是一个任务，可以对教学计划进行管理。

图3 经初等变换后的块下三角阵

1.3 教学计划进程数学模型的建立

教学计划进程之间的关系与工程设计之间的关系极为相似，同样可以采用设计结构矩阵建立相应的数学模型。本文以生命科学与化学工程学院化工专业的教学计划进程为例，说明DSM在教学计划安排中的应用。为使分析结果表达简明，仅采用十四门课程构成结构矩阵，略去有明确安排的课程，选取那些在一定程度上有相关性的专业课程，见表2。

把表2写成结构矩阵形式，图中左面为原始结构矩阵，右面为经初等变换后的结构阵。

经变换后可以明显地看出课程之间的顺序关系，其中课程E和H及(具体课程名称如图，下同)之间没有耦合关系，可以并行地执行，其后的顺序分别是:A—M—C—J—I。其中还可以看出H、A、M之间也没有依赖(构成的下三角区中元素为0)，因而也可以并行执行。而E、D、K三课程构成了一个矩阵块，因而必须看成一个任务来执行，在计划安排时，可以把它们安排在同一时间段内执行。同样情况的还有H和I构成的块。

合理的顺序是:B—H—A—M—C—J—I—E—D—K—F—N—L—G，这些课程就这样被合理地安排了。

上述DSM中，H、A、M之间有相关性，因而可以并行地执行，在教学安排中相对来说比较好处理，而EDK、NL构成的矩阵块表达了相互之间的紧密耦合关系，这也是任务矩阵中最难处理的部分。在教学计划安排中，要求把这部分的任务安排在同一时间段(如同一学期)中完成，以保证课程之间的正常信息传递。当课程任务矩阵中有很多这样的课程紧密地耦合在一起的时候，就需要专门的手段加以解耦(由于牵涉到较多较深的数学理论，限于篇幅，本文不作阐述，将另文分析)。

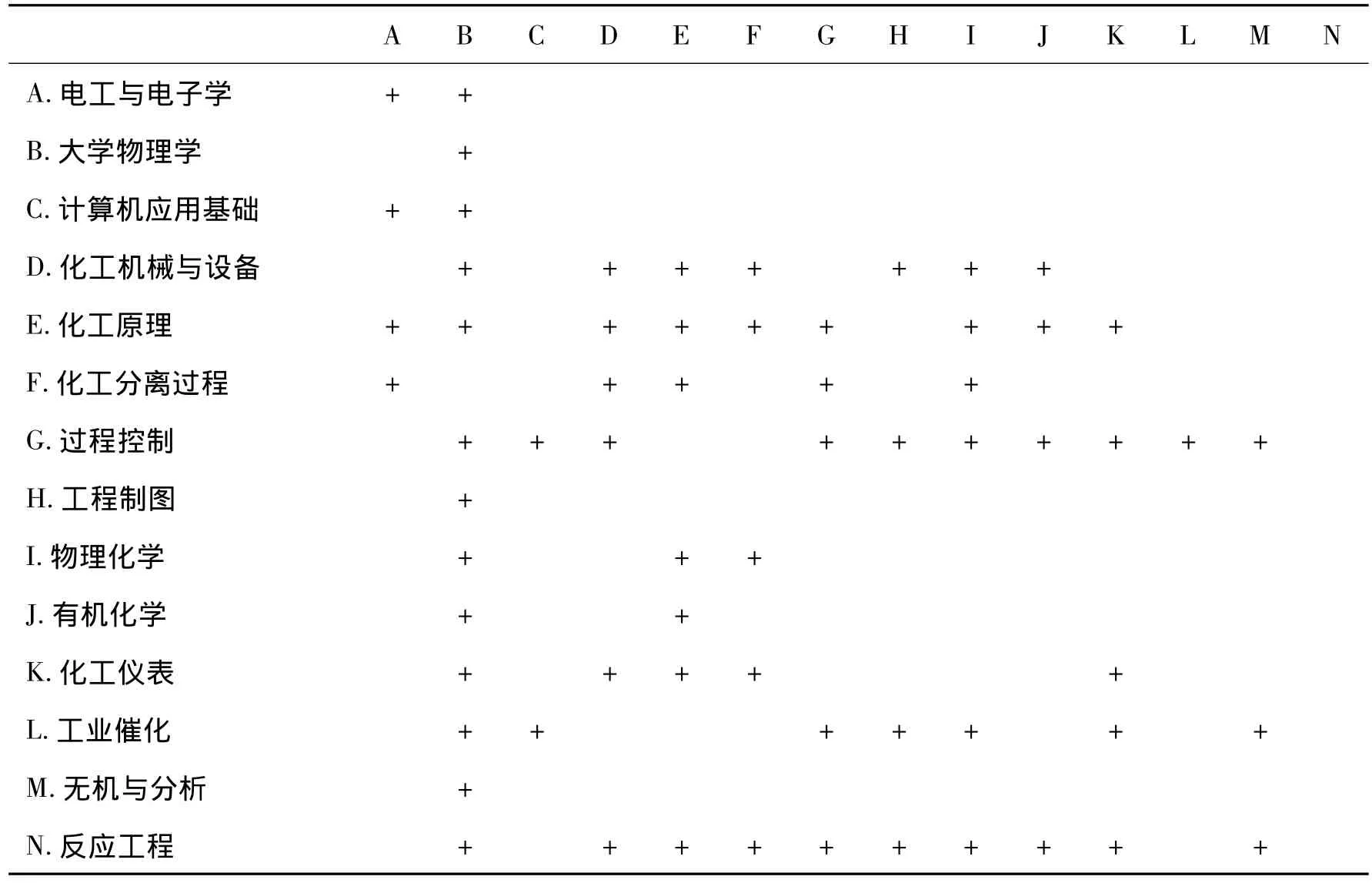
表2 课程相关性表

图4 教学计划安排设计结构矩阵

2 结构矩阵分析的程序设计

由于对课程建立了相关的数学模型，将教学计划安排转化为数学问题，因而可以编制相应的计算机程序来进行矩阵分析。

由于教育计划安排实用程序的使用者通常都不是计算机专业人员，因而要求程序有良好的人机界面和较强的易用性，可以采用VB进行有关程序设计，见图5。

程序结构简要说明如下:①键盘输入需要规划的课程名称;②查询数据库，如果数据库中有相关表就调出，如果没有即输入相关表;③自动生成原始设计结构矩阵(Original DSM);④对原始设计结构矩阵进行分析，获得最后的final DSM;⑤存入数据库，为以后的安排进行数据储备;⑥ 输出结果。

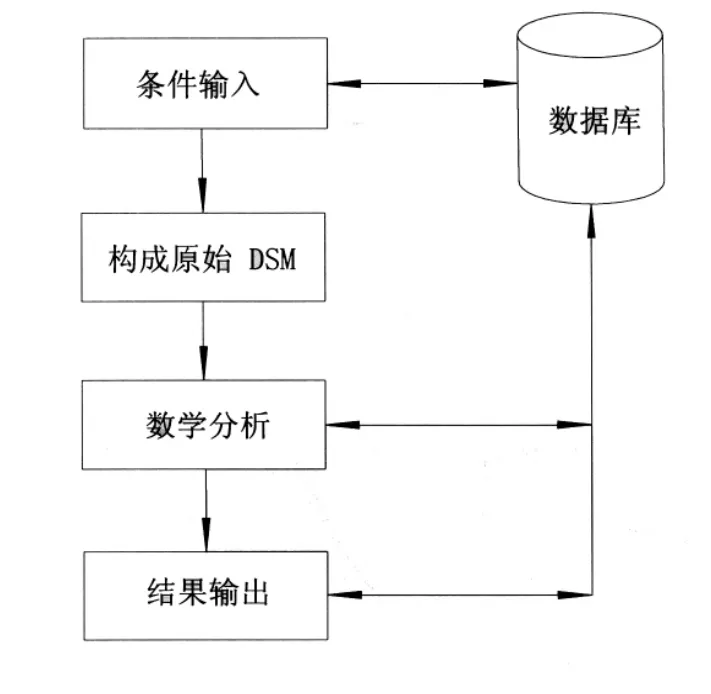
图5 程序的结构示意图

3 结论

采用DSM方法进行教学计划进程的安排，由于采用了数学模型，将复杂的教学计划安排问题数字化，便于计算机管理，使决策更加快速、科学，符合管理现代化的方向。DSM方法很直观地表达了课程之间的相互关系，不仅对教学计划的制订有指导作用，而且使教学计划的执行者更加明确了课程之间的内在联系，使教学过程更加优化。采用设计结构矩阵的方法，不仅可以适应新的专业教学计划安排，而且可以对原教学计划进行分析，根据分析结果优化进程。

参考资料:

［1］D.V.Steward.The Design Structure System:A Method for Managing the Design of Complex System［J］.IEEE Transaction on Engineering Manage.1981，28(3):71－74.

［2］T.U.Pimmmler，S.D.Eppinger.Integration Analysis of Product Decompositions［J］.ASME Conference on Design Theory and Methodology，1994，68(11):345 －351.

［3］原慧琳，汪定伟.基于实值设计结构矩阵算法进行流程的优化设计［J］.系统工程，2010(3):69－72.

［4］金烨，李玉家.并行任务的组织规划综述［J］.制造业自动化，2000，22(12):22 －28.

［5］董明，查建中，郭伟.并行工程中的任务组织［J］.系统工程理论与实践，1996(8):69－78.

［6］鄂明成，查建中，郭伟.并行设计中作业量与时间模型的研究［J］.计算机辅助设计与图形学学报，1997，19(2):104－120.

［7］许以超.线性代数与矩阵论［M］.北京:高等教育出版社，1992:154，165.