西部地区大学生科学推理能力研究——以宁夏大学为例

张轶炳，白明侠，黄 昭

(1.宁夏大学 物理电气信息学院;2.教育学院，银川750021)

0 引言

科学推理能力是科学素养的重要组成部分，是现代社会每个人应该具备的思考问题的方法和能力，对于实现人的科学发展具有重要意义。科学推理(Scientific Reasoning)的概念由皮亚杰在其认知发展理论中首次提出。至今，科学推理能力仍是国外心理学、教育学、教育心理学等研究的一个重要领域，但国内研究却很少涉猎。

个体的科学推理能力发展与很多因素有关，间接或直接地与皮亚杰的发展认知理论联系。纵观历史，认知发展心理学家与科学教育研究者们发现有很多因素都影响着科学推理能力的发展。

本文从整体上对宁夏大学学生的科学推理及各维度成绩进行分析，探讨性别、年级、专业等因素是否对科学推理能力及各维度能力有显著影响。

1 对象与方法

1.1 对象

在宁夏大学随机抽取570名本科生进行调查，回收问卷570份，获得有效问卷558份，有效回收率 97.89%。

1.2 工具

本研究采用的科学推理能力的测试卷是俄亥俄州立大学(OSU)LeiBao教授等对Anton.E Lawson编制的科学推理测试卷改进的中文版。本次测试采用G卷，共30个选择题，包含科学推理能力的七个维度的测量，包括控制变量推理、概率推理、相关推理、假设演绎推理、逻辑推理、多层次假设推理及原因关联，Anton.E Lawson编制的科学推理能力测试卷在全世界被广泛应用，被认为具有良好的效度和信度。试卷中维度构成见表1。

表1 试卷维度构成表

1.3 方法

采用俄亥俄州立大学(OSU)LeiBao教授等人修订的中文版科学推理能力测试问卷(G卷)。该问卷均为选择题，需要被试者仔细阅读题目，选择合适答案，得分越高，表明该生的科学推理能力越强。在任课老师的协助下，将科学推理能力测试题试卷发放给被试者，在课堂上进行集体施测，统一指导语。全部数据资料采用SPSS.16.0统计软件进行统计分析。

由于测试数据均为原始数据，需要量化评分后才能进行分析研究。原始数据不进入统计过程，统计考虑的数据为科学推理及各维度能力得分。针对此次数据的特点，笔者们主要分析性别、年级、专业等对科学推理成绩及各维度的影响。

2 结果

2.1 科学推理能力成绩总体分析

在558份问卷中，最高分86.67，最低分12.50，平均分约为42.58，相对(OSU)LeiBao 教授所测得的中国地区科学推理能力的平均成绩:74分(样本取样于北京交通大学、同济大学、北京师范大学和清华大学等)低很多，由此得出宁夏大学学生的推理能力比同年级的东部地区大学的成绩要低。科学推理能力成绩的Kolmogorov－Smirnov检验显著性水平 Sig.为0.000，Shapiro－Wilk检验显著性水平 Sig.为 0.001，都远小于 0.05，从而拒绝变量成绩服从正态分布。

由于成绩的分布不符合正态分布，还需要选择非参数检验对其进行进一步的分析。

2.1.1 按照性别的两独立样本的非参数检验

从曼–惠特尼U检验的秩统计量表得出男生为345人，女生为213人，平均秩次分别为286.57与281.07，由此可以粗略看出男生和女生在科学能力成绩相差不大。曼－惠特尼U(Mann－Whit ney U)双尾渐进显著性概率为0.698，远大于0.05。柯尔莫哥洛夫－斯米尔诺夫Z检验的双尾渐进显著性概率为0.661，也远大于0.05，按照检验结果的判断规则，应接受原假设，见表2。

表2 曼–惠特尼U检验与柯尔莫哥洛夫–斯米尔诺夫Z检验结果表a

从曼–惠特尼U检验结果与柯尔莫哥洛夫–斯米尔诺夫Z检验结果都得出宁夏大学学生在性别上对科学推理能力没有显著影响，这与Ehindero(Ehindero，1982)的研究结果相同。

2.1.2 多个独立样本的非参数检验

由于年级与专业的分组较多，所以采用多个独立样本的非参数检验，分别对年级与专业是否影响科学推理能力进行分析，结果见表3。

表3 克鲁斯凯–沃里斯H检验与中位数检验结果表a

由表3可以看出，克鲁斯凯—沃里斯H检验结果的渐进显著性概率为0.000，远小于0.05，中位数检验的渐进显著性概率为0.000，也远小于

0.05，应拒绝原假设。综合两种检验方法的结果，可以认为年级的差异对科学推理能力有显著的影响。同理可以得到专业的独立样本的非参数检验:克鲁斯凯–沃里斯H检验渐进显著性概率为0.005，中位数检验的渐进显著性概率为0.010，均小于0.05，拒绝原假设。综合两种检验方法的结果，可以认为专业的差异对科学推理能力有显著的影响。

2.1.3 年级与专业的多样本的两两比较

年级与专业的内部分类均属于多样本，当各组例数较多时，可以采用秩变换分析，操作更加方便，且结论也更加准确。所谓秩变换分析方法，就是先求出原变量的秩次，然后使用求出的秩次代替原变量进行参数分析，当样本含量较大时，该方法的分析结果和相应的非参数方法基本一致，但该方法可以充分利用己知的参数方法，如多组样本的两两比较、多元回归等，从而大大扩展了非参数分析方法的范围。

由于该样本一共有558例，样本量较为充足，因此考虑直接使用秩变换方法加以分析，即首先求出科学推理成绩的秩次，然后进行方差分析。

表4 秩次方差分析结果表

从秩次方差分析结果表(表4)中可以看出对秩次进行方差分析的结果:专业的组间显著性概率 Sig.为 0.000，年级的显著性概率 Sig.为 0.004，均远小于0.05，拒绝接受原假设，即科学推理能力的秩次在不同专业与年级间的差别是有统计学意义的。认为不同年级、不同专业的科学推理能力有差异。接下来对专业与年级的多样本进行两两比较的研究，结果见表5。

表5 专业秩统计量表

从专业秩统计量表与专业多重比较检验表中可知，有些专业之间差异明显，有些则无显著差异。考虑样本各专业容量不同，可能影响专业间的比较。选择容量较相近的进行比较，电气信息(135人)和物理教育(117人)样本容量相近，样本量相对较大，显著性概率 Sig.为0.002，远小于 0.05，两个专业间存在显著差异。而其余各专业由于样本量偏小，本文不予对比分析。由此得出当样本容量相接近时，专业差异对科学推理能力有显著性差异。从专业秩统计量表(表5)可以看出电子信息、机械、交通运输等工科专业的平均秩值比其他专业高，即:工科专业的科学推理能力水平较高。

表6年级秩统计量表

表7 年级多重比较检验表

从年级秩统计量表(表6)和年级多重比较检验表(表7)中可以看出，大二与大三样本容量分别为106人、105人，有可比性，显著性差异为Sig.为0.000，小于 0.05，拒绝原假设。由此得出大二与大三之间有显著性差异。而大一和大二、大一和大三之间由于样本容量差异较大，可能存在误差。因此，可以认为宁夏大学大三学生同另两个年级间存在显著差异。

2.2 科学推理能力各维度的成绩分析

2.2.1 多个相关样本的非参数检验

根据弗里德曼的双向评秩方差分析，由表8可以得出，渐进显著性概率为0.000，远小于0.05，拒绝原假设，即科学推理成绩及不同维度成绩之间存在显著差异。

表8 弗里德曼检验统计量表a

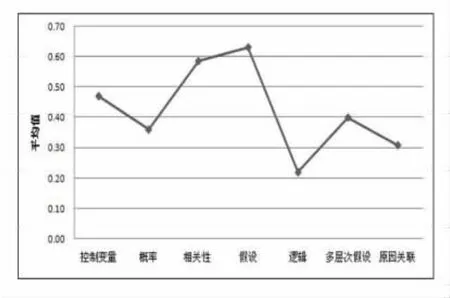
图1 各维度推理成绩的平均值分布曲线

由图1可以明显看出，学生们各维度的平均成绩分布不均，即学生们各维度科学推理成绩发展不均衡。得分最低的为逻辑推理成绩，学生们的逻辑推理能力较欠缺。

2.2.2 按性别区分的各维度的两独立样本的非参数检验

由克鲁斯凯–沃里斯检验结果表可以看出(见表9)，性别对各维度的推理成绩基本上没有显著影响，只有控制变量推理显著性概率为0.009，小于0.05，拒绝原假设。即性别的差异对控制变量推理有显著性影响。

表9 克鲁斯凯—沃里斯检验结果a

根据线图(图1)显示可以进一步看出，男生在控制变量、假设、原因关联及逻辑推理这四个维度中，平均成绩高于女生。而女生在概率、相关性、多层次假设等维度的平均成绩要高于男生。

2.2.3 多个独立样本的非参数检验

由于年级与专业的分组较多，所以采用多个独立样本的非参数检验，分别对年级与专业是否影响科学推理各维度的成绩进行分析。

表10 克鲁斯凯—沃里斯检验结果表a，b

由表10可以看出，不同年级的科学推理各维度基本上没有显著性差异，只有概率推理与多层次假设推理的显著性概率为0.000，远小于0.05，即可以认为不同年级学生在概率推理及多层次假设推理的维度上有显著差异。

由图1可以明显看出，随着年级的增长，多层次假设、相关性、概率、控制变量、假设等维度的推理成绩都有上升的趋势。但逻辑推理、原因关联等呈明显的下降趋势。

表11 克鲁斯凯——沃里斯检验结果表a，b

由表11可以看出，不同专业的学生在科学推理各维度上基本没有显著性差异。在概率推理、相关性推理、多层次假设推理上的显著性概率均小于0.05，即有显著性差异。

3 讨论

3.1 各维度发展不均衡，逻辑推理欠缺

图2为逻辑推理所描述的推理背景，逻辑推理的第一题是根据条件“如果纸牌的一面为偶数，那么翻过来的那面对应的一定是灰色。”来选择最少需要翻哪张牌或哪几张牌来检验上述判断，学生的正确率为24.55%，约有44.68%选择了“翻8和灰色的那张”的错误选项，约有21.28%的学生选择了“把所有的牌都翻开”的错误选项。

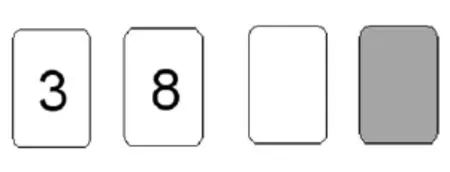
图2 纸牌实验

研究表明:选择了“把所有的牌都翻开”的学生头脑中并未进行任何推理过程，一部分是凭借直觉进行的选择，另一部分是对七个选项举棋不定，对条件与结果的分析缺少合理的推理判断，最终选择把所有的牌都翻开。选择了“翻8和灰色的那张”错误选项的学生占了大多数，即多数学生能对简单、明显的论题给出正确的判断，但涉及进一步的推理过程:应该翻白色还是灰色的牌时，学生判断错误。学生们忽略了从所给的已知条件来深入推理。学生大脑中没有有效建构解决逻辑推理问题的认知策略。当他们面对实际的逻辑推理背景时，不能确定正确的推理方式，从而给出错误的推理结果。

3.2 按照性别区分主要存在的差异

男女生在控制变量推理能力方面有显著的差异。控制推理的平均成绩为0.4700，男生的控制推理的平均成绩为0.4964，高于总体平均成绩的为52.98%。女生的平均成绩为0.4272，高于总体平均成绩的为46.78%，相差将近6个百分点。

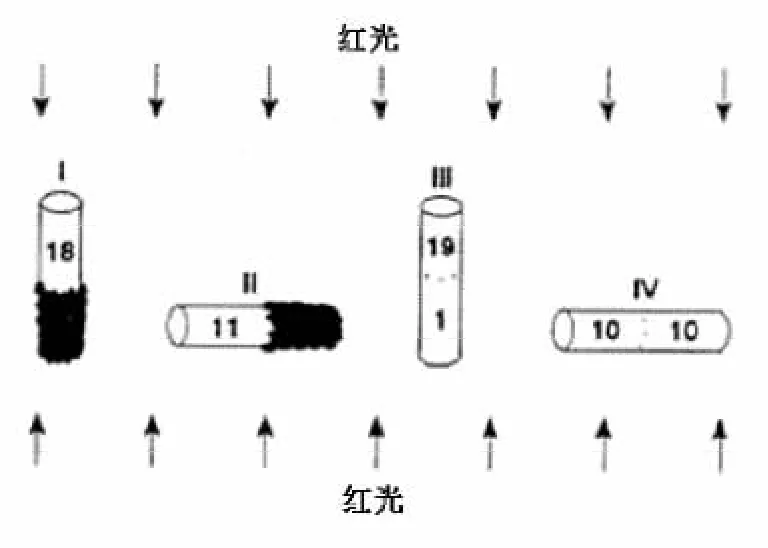
图3 果蝇实验

对比控制变量中果蝇实验的两个题目可以发现(见图3)，实验中主要涉及重力与光两个因素，学生要通过试管中果蝇的数量来判断两个因素的作用情况。但男女学生的正确率却大不相同，女生的正确率为44.95%，男生的正确率为61.51%。

研究发现:女生对题目进行分析时，主要是凭借直觉与回忆相关知识来判断，并未深入研究题目条件与所给的证据进行推理得到，即学生并未从正确答案的根本原因中推出结论。例如:女生此题的正确率为44.95%，而原因选择的正确率却为49.54%。比例为1∶1.1，而男生的比例约为1∶1。即有些女生并不是靠证据进行推理，在推理过程中也未考虑证据和结论之间的一致性。而这正是科学推理的特征。有些学生对科学推理的本质特征缺乏认识，反映出大学教学中对推理本质教育的缺失。

3.3 按照年级、专业区分主要存在的差异

由曼–惠特尼U检验结果得出年级与专业的不同对概率推理与多层次假设推理均有显著性差异。从图4可以明显看出对于不同年级学生的概率与多层次假设推理的平均成绩也有显著的不同。

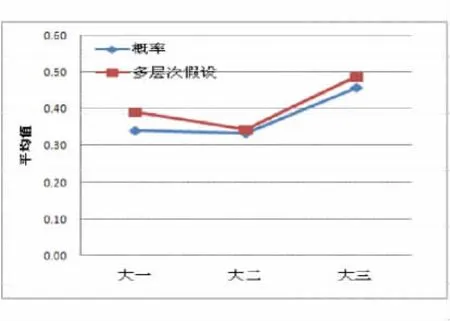
图4 不同年级的概率推理与多层次假设推理平均值线图

研究发现:一是学生对概率统计的知识背景相当匮乏。除特定专业，如交通运输、物理等接受过初步的概率统计知识，其余学生完全凭借自己的生活经验进行选择。二是所学习的概率统计知识过于抽象，与现实生活脱节，导致学生完全凭借书本知识进行判断，并未根据题目中所给出条件及证据进行推理。

科学推理能力受到很多因素的影响，本次研究分析了性别、专业、年级与科学推理能力及各维度之间的关系。总体上得到这样的结论:即大学生的性别差异对科学推理能力基本上没有显著性影响，只有在控制变量推理方面有显著性差异;专业与年级的差异对科学推理能力有显著的影响，主要表现在概率推理与多层次假设推理上。工科的科学推理能力较其他专业高，随着年级的升高，科学推理水平及各维度均有增加的趋势。本次测试分析样本数量虽大，但分布不均，造成部分分析结论不够精确，有待增加样本容量后继续分析。

［1］严文法，胡卫平.国外青少年科学推理能力研究综述［J］.外国中小学教育，2009(5):23 －28.

［2］Tronie Rifkin，John Harry Georgakakos.Science Reasoning Ability of Community College Students［J］.ERIC Clearinghouse for Community Colleges，2001(2):221 －224.

［3］Resnick，L.B.＆Gelman，R.Mathematical and Scientific Knowledge:An Overview Pittsburgh，PA:Pittsburgh U-niversity［J］.Learning Research and Development Center，1985(ED):258 －262.

［4］Finegold，M.＆Mass，R.Differences in the Processes of Solving Physics Problems Between Good Physics Problem Solvers and Poor Physics Problem Solvers［J］.Research in Science and Technological Education，1985，3(1):59 －67.

［5］Stuessy，C.Correlates of scientific reasoning in adolescents:Experience，locus of control，age，field dependence independence，rigidity/flexibility，IQ，and gender Columbus，OH:Doctoral dissertation［J］.The Ohio State University，1984(ED):244－248.

［6］Lawson，A.E.Formal reasoning，achievement，and intelligence:An issue of importance［J］.Science Education，1982，66(1):77 －83.

［7］Cherian，V.I，Kibria and so on，T.S.Formal operational reasoning in African university students［J］.The Journal of Psychology，1988，122(5)487－498.

［8］ Acuna，J.E.Acculturation，Social class and cognitive growth.Quezon city，Philippines:Philippines University［J］.Science Education Center，1983(ED):239 －241.

［9］Lei Bao，Tianfan Cai and so on，Learning and Scientific Reasoning［J］.SCIENCE，2009，323:586 －587.

［10］Ehindero，J.O.Correlates of gender－ relates differences in logical reasoning［J］.Journal of Research in Science Teaching.1982，19(7):553 －557.

［11］张文彤，闫洁.SPSS统计分析基础教程［M］.北京:高等教育出版社，2004:9.

［12］杨燕，郭玉英，魏昕.高师理科教学与学生科学推理能力的培养［J］.教育学报，2010(4):42－47.