基于滑模变结构的一类非最小相位系统控制

孙保良，邢福成

（海军航空工程学院电子信息工程系，山东 烟台 264001）

0 引言

从非线性控制理论的角度看，如果零动态不稳定，那么系统就是非最小相位系统。

处理非最小相位问题的方法有很多[1-11]，但是怎样有效地解决非最小相位系统的控制问题一直受到人们的普遍关注。

在传统处理非最小相位方法中，根据经典的控制理论，国内的许多专家学者提出了多种的处理非最小相位问题的方案。由于非最小相位系统的不稳定零点给前馈控制器的设计带来了很大的困难，零相位误差跟踪控制器(ZPETC)[12]的提出，部分地解决了这一问题。为了进一步提高跟踪精度，减小幅值误差，提出了调幅滤波器，与ZPETC串联构成零幅相误差跟踪控制器，理论上可实现理想跟踪控制，即输出可以完全复现输入信号。文献[13]基于最小方差预报理论和极点配置原理，提出了一种类似组合自校正器[14-15]的自适应控制方案，消除了组合自校正器跟踪参考信号时所发生的滞后现象[12，16]，而且仍然保存了现有极点配置控制器的优点，从而克服了设计自适应控制器无法兼顾伺服跟踪性能和随机调节性能皆优的缺点。文献[13]针对一类自衡二阶非最小相位过程，采用内模控制系统结构，使系统具有良好的抗扰性和鲁棒性，并且给出了在希望的幅值和相角裕量下控制器参数的计算方法。文献[17]利用中科院系统所韩京清提出的一种非线性控制律：针对自抗扰控制器(ADRC)对倒立摆、水轮机调速器、鱼雷定深、飞机高度及直升机俯仰角控制等对象模型，分别设计了自抗扰控制器。研究发现，只要对控制器的设计略加改造，ADRC对上述对象都具有满意的控制性能。文献[18]从输出的角度考虑，由于对于单输入—单输出系统，它的零点取决于系统的输出函数，在系统的输出端并联一个常数阵，通过利用可观测性阵讨论它对可观测性性能的影响。证明了在满足适当的条件下，可以任意配置零点，从而可以将一个非最小相位系统变成最小相位的系统。并成功地将这种设计方法用于飞机的高度动态性能补偿，该方法类似于输出重定义。本文基于反馈线性化的思想将其转换为规范型，提出了采用滑模面对其输出进行了重定义设计的一种复合控制方案，仿真结果表明，该复合控制算法具有较高的控制精度。

1 一类非最小相位系统问题的描述

设单输入单输出(SISO)非线性系统

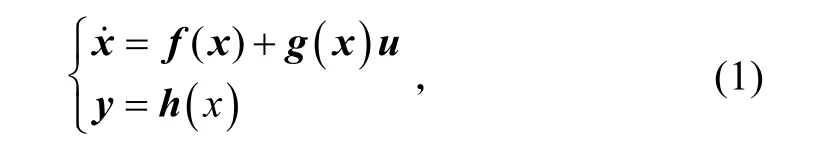
式中：状态 x ∈Rn；输出y∈R，yc(t)为其参考轨迹；f (x)、h (x)为具有适当维数的充分光滑的函数向量，且满足 f (0)=0，且系统(1)满足下面假设。

假设1：非线性系统(1)具有适定的(Well-defined)相对度r，满足0＜r＜n，则在原点的开邻域内满足

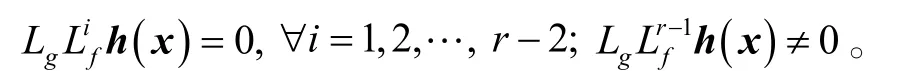
假设2：非线性系统(1)为非最小相位系统。

定义1：如果则系统1 输出实现了精确跟踪；

定义2：当t→∞时，如果则系统(1)输出实现了渐近跟踪。

2 基于反馈线性化的规范型转换

对n阶非线性系统(1)，相对度为r，先将其转化为规范形。

为叙述方便，采用如下表示，李导数：

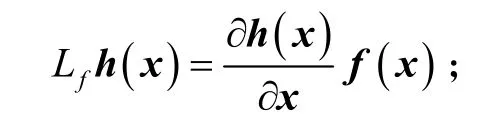
多重李导数：

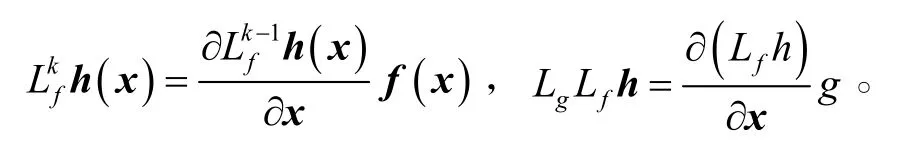
通过非线性坐标变换

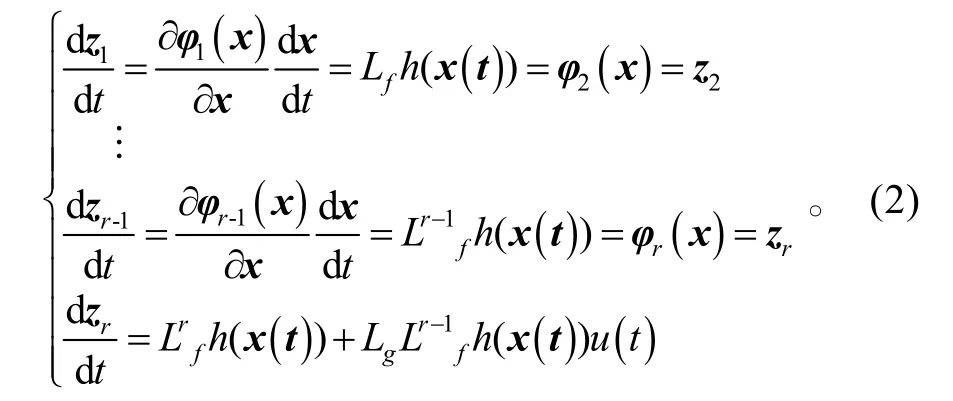
对于式(2)最后一个方程，将 x (t)表示成 z (t)的函数，即 x (t)=Φ−1(z (t))。这样，令

剩余的n−r个坐标，由于

令

前述的方程可以写成

系统(1)经坐标转换 z=Φ(x)可以写成下式

式中：Φ(x)为微分同胚，且满足 Φ(0)=0。令

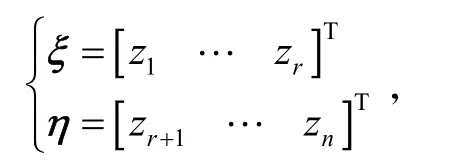
则式(5)可写成

将式(6)式中关于η的微分方程展开，则系统(6)可写成

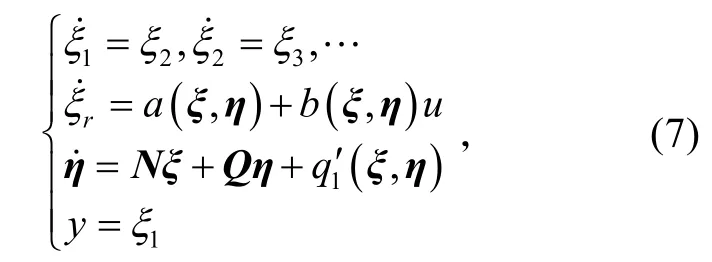
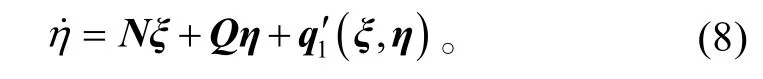
3 滑模面输出重定义的设计

由假设2可知，Q 有正实部特征值。定义滑模面为系统的新输出

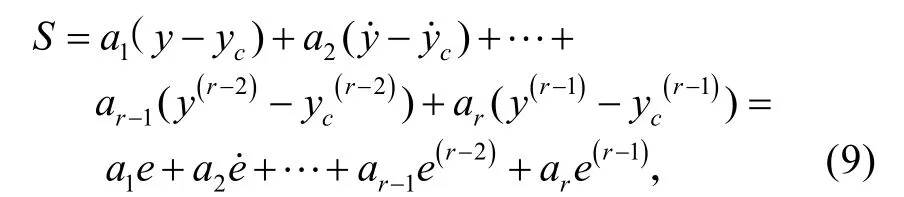
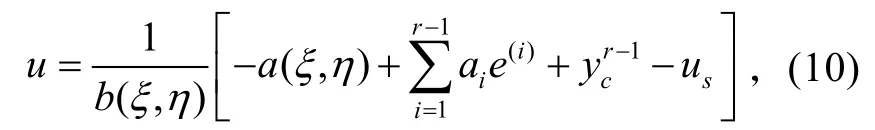
式中，us=k1sgn(S)+k2S,k1＞0,k2＞0。

由式(7)和式(10)可得

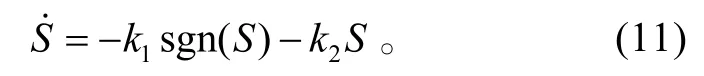
令

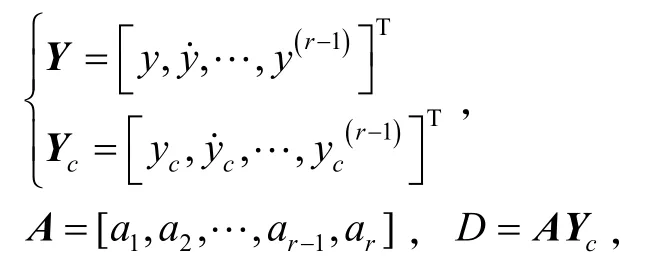
则

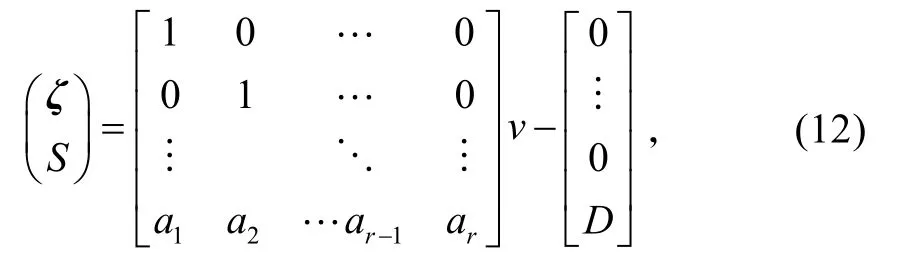
式中：ζ ∈ Rr−1；S ∈R。

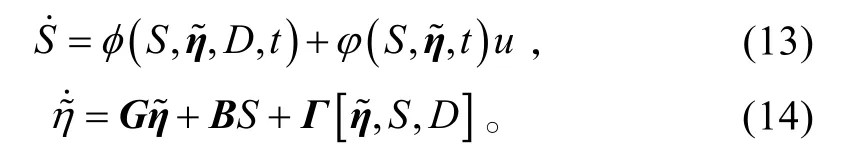
4 举例仿真

现在以某型导弹法向过载控制为例进行控制系统的设计和仿真。

以某型反舰导弹在1 000 m高度平飞状态的特征点数据进行仿真。假设舵机的传递函数为17 (s+17)。期望响应 nyd由标准二阶振荡环节滤波得到式中：r为指令输入；ξ=0.707；ω=13 rad/s。取滑动面为为了验证该设计方法的正确性和有效性，分别对参数摄动和输入为方波信号的情况进行了仿真，仿真结果分别如图1、图2所示。

图1 导弹过载跟踪变化图

图2 导弹wz变化图

5 结束语

基于反馈线性化和变结构控制理论，针对一类非最小相位的非线性系统，提出了一种复合控制方案。首先，基于反馈线性化的思想将其转换为规范型，采用滑模面对其输出进行了重定义设计；最后，为了验证该复合控制的有效性和正确性，基于某型导弹的非最小相位系统进行了仿真计算。仿真结果表明，该复合控制算法具有较高的控制精度。

[1]KRAVARIS C,WRIGHT R A.Nonminimum-phase compensation for nonlinear processes[C]//AIChE J.1992,38∶26.

[2]SHKOLNIKOV I,SHTESSEL Y B.Aircraft nonminimum phase control in dynamic sliding manifolds[J].Guid.Contr.Dyn.,2001,24(3)∶64-71.

[3]Tip-trajectory tracking control of single-link flexible robots via output redefinition[C]//Proceedings of the 1999 IEEE.International Conference on Robotics and Automation Detroit.Michigan,1999.

[4]ZINOBER A,OWENS D.Nonlinear and Adaptive Control[C]//LNCIS.Springer-Verlag Berlin Heidelberg,2003∶239-248.

[5]HUANG J,RUGH W J.On a nonlinear multivariable servomechanism problem[J].Automatica,1990,26∶963-972.

[6]GOPALSWAMY S,HEDRICK J K.Tracking nonlinear non-minimum phase systems using sliding control[J].International Journal of Control,1993,57(5)∶1141-1158.

[7]ZHENG TAODING.Backstepping stabilization of nonlinear systems with a nonminimum phase zero[C]//Proceedings of the 40th of IEEE conference on Decision and Control Orlando.Florida USA,2001.

[8]IIYA A SHKOLNIKOV,YURI B SHTESSEL.Aircraft nonminimum phase control in dynamic sliding manifolds[J].Journal of guidance,control and dynamics,2001,24(3)∶566-572.

[9]CHWA D K,CHOI J Y.New parametric affine modeling and control for skid-to-turn missiles[C]//IEEE Transactions on Control Systems Technology,2001,9(2)∶335-347.

[10]LEE J I,HA I J.Autopilot design for highly maneuvering STT missiles via singular perturbationlike technique[J].IEEE Transactions on Control System Technology,1999,7(5)∶527-541.

[11]RYU J H,PARK C S,TANK M J.Plant inversion control of tail-controlled missiles[C]//Guidance,Navigation and Control Conferrnce.New orleans,1997∶1691-1696.

[12]马骋,冯之敬,赵广木.零幅相误差跟踪控制器[J].清华大学学报∶自然科学版,2000,40(5)∶44-46.

[13]蔡秀珊,阮荣耀,非最小相位系统的自适应跟踪 Ⅰ∶单输入单输出情况[J].华东师范大学学报∶自然科学版,2000(9)∶27-32.

[14]李清泉.组合自校正器[J].自动化学报,1986,12(2)∶138-145.

[15]张维存,李清泉.多变量组合自校正器[J].信息与控制,1994,23(3)∶129-132.

[16]鲁照权.一类非最小相位过程内模控制系统设计[J].基础自动化,2002,9(2)∶7-10.

[17]刘翔,李东海,姜学智,胡雪蛟.不稳定对象及非最小相位对象的自抗扰控制仿真研究[J].控制与决策,2001,16(4)∶420-429.

[18]谢世杰,唐小静,吴旭光,徐德民.零点配置和飞行器高度动态系统的性能补偿[J].系统工程与电子技术,2000,22(11)∶29-30.